有 k 种颜色的涂料和一个包含 n 个栅栏柱的栅栏,请你按下述规则为栅栏设计涂色方案:
- 每个栅栏柱可以用其中 一种 颜色进行上色。
- 相邻的栅栏柱 最多连续两个 颜色相同。
给你两个整数 k 和 n ,返回所有有效的涂色 方案数 。
示例 1:
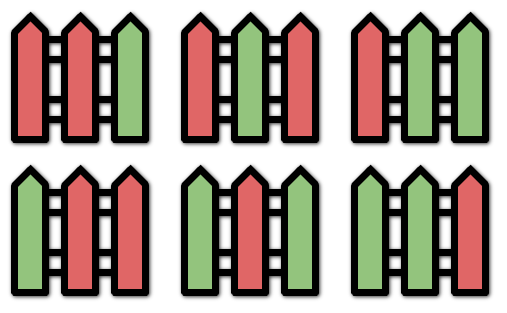
输入:n = 3, k = 2 输出:6 解释:所有的可能涂色方案如上图所示。注意,全涂红或者全涂绿的方案属于无效方案,因为相邻的栅栏柱 最多连续两个 颜色相同。
示例 2:
输入:n = 1, k = 1 输出:1
示例 3:
输入:n = 7, k = 2 输出:42
提示:
1 <= n <= 501 <= k <= 105- 题目数据保证:对于输入的
n和k,其答案在范围[0, 231 - 1]内
方法一:动态规划
定义
初始时
答案为
时间复杂度
class Solution:
def numWays(self, n: int, k: int) -> int:
dp = [[0] * 2 for _ in range(n)]
dp[0][0] = k
for i in range(1, n):
dp[i][0] = (dp[i - 1][0] + dp[i - 1][1]) * (k - 1)
dp[i][1] = dp[i - 1][0]
return sum(dp[-1])class Solution {
public int numWays(int n, int k) {
int[][] dp = new int[n][2];
dp[0][0] = k;
for (int i = 1; i < n; ++i) {
dp[i][0] = (dp[i - 1][0] + dp[i - 1][1]) * (k - 1);
dp[i][1] = dp[i - 1][0];
}
return dp[n - 1][0] + dp[n - 1][1];
}
}class Solution {
public:
int numWays(int n, int k) {
vector<vector<int>> dp(n, vector<int>(2));
dp[0][0] = k;
for (int i = 1; i < n; ++i) {
dp[i][0] = (dp[i - 1][0] + dp[i - 1][1]) * (k - 1);
dp[i][1] = dp[i - 1][0];
}
return dp[n - 1][0] + dp[n - 1][1];
}
};func numWays(n int, k int) int {
dp := make([][]int, n)
for i := range dp {
dp[i] = make([]int, 2)
}
dp[0][0] = k
for i := 1; i < n; i++ {
dp[i][0] = (dp[i-1][0] + dp[i-1][1]) * (k - 1)
dp[i][1] = dp[i-1][0]
}
return dp[n-1][0] + dp[n-1][1]
}