Given the root of a binary tree, return the sum of every tree node's tilt.
The tilt of a tree node is the absolute difference between the sum of all left subtree node values and all right subtree node values. If a node does not have a left child, then the sum of the left subtree node values is treated as 0. The rule is similar if the node does not have a right child.
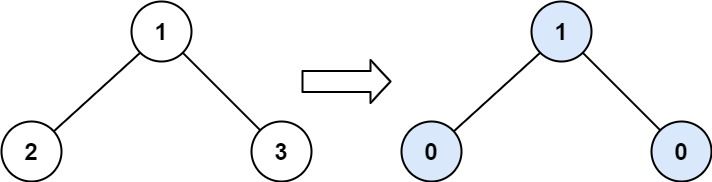
Example 1:
Input: root = [1,2,3] Output: 1 Explanation: Tilt of node 2 : |0-0| = 0 (no children) Tilt of node 3 : |0-0| = 0 (no children) Tilt of node 1 : |2-3| = 1 (left subtree is just left child, so sum is 2; right subtree is just right child, so sum is 3) Sum of every tilt : 0 + 0 + 1 = 1
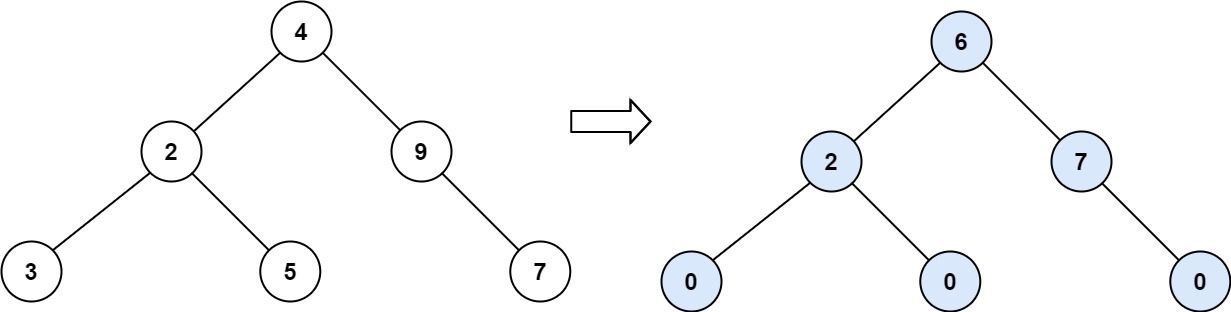
Example 2:
Input: root = [4,2,9,3,5,null,7] Output: 15 Explanation: Tilt of node 3 : |0-0| = 0 (no children) Tilt of node 5 : |0-0| = 0 (no children) Tilt of node 7 : |0-0| = 0 (no children) Tilt of node 2 : |3-5| = 2 (left subtree is just left child, so sum is 3; right subtree is just right child, so sum is 5) Tilt of node 9 : |0-7| = 7 (no left child, so sum is 0; right subtree is just right child, so sum is 7) Tilt of node 4 : |(3+5+2)-(9+7)| = |10-16| = 6 (left subtree values are 3, 5, and 2, which sums to 10; right subtree values are 9 and 7, which sums to 16) Sum of every tilt : 0 + 0 + 0 + 2 + 7 + 6 = 15
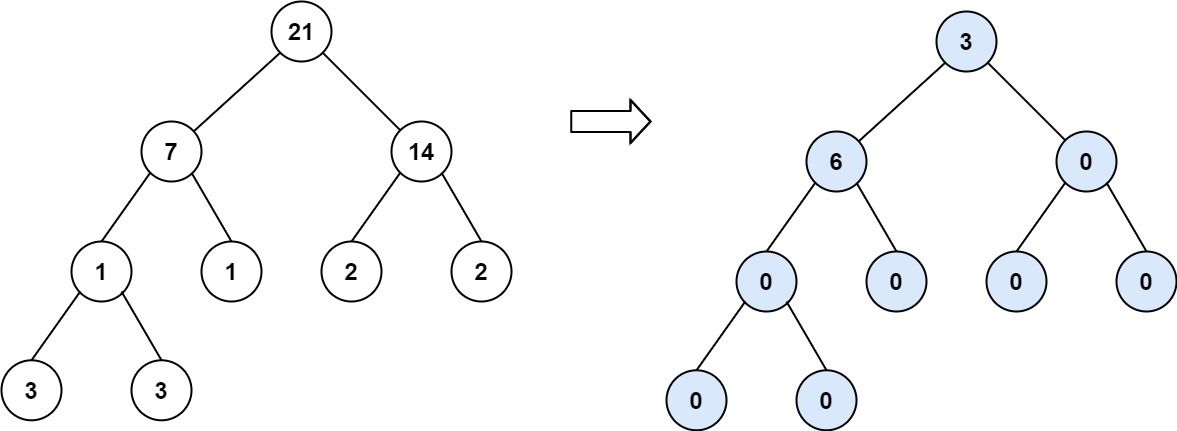
Example 3:
Input: root = [21,7,14,1,1,2,2,3,3] Output: 9
Constraints:
- The number of nodes in the tree is in the range
[0, 104]. -1000 <= Node.val <= 1000
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def findTilt(self, root: TreeNode) -> int:
ans = 0
def sum(root):
if root is None:
return 0
nonlocal ans
left = sum(root.left)
right = sum(root.right)
ans += abs(left - right)
return root.val + left + right
sum(root)
return ans/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private int ans;
public int findTilt(TreeNode root) {
ans = 0;
sum(root);
return ans;
}
private int sum(TreeNode root) {
if (root == null) {
return 0;
}
int left = sum(root.left);
int right = sum(root.right);
ans += Math.abs(left - right);
return root.val + left + right;
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int ans;
int findTilt(TreeNode* root) {
ans = 0;
sum(root);
return ans;
}
int sum(TreeNode* root) {
if (!root) return 0;
int left = sum(root->left), right = sum(root->right);
ans += abs(left - right);
return root->val + left + right;
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
var ans int
func findTilt(root *TreeNode) int {
ans = 0
sum(root)
return ans
}
func sum(root *TreeNode) int {
if root == nil {
return 0
}
left, right := sum(root.Left), sum(root.Right)
ans += abs(left - right)
return root.Val + left + right
}
func abs(x int) int {
if x > 0 {
return x
}
return -x
}