Skip to content

Latest commit

 

History

History
118 lines (91 loc) · 6.42 KB

lda_on_angel.md

File metadata and controls

118 lines (91 loc) · 6.42 KB

LDA*（Latent Dirichlet Allocation）

LDA是一种常见的主题模型算法。简单来说它是一个贝叶斯概率生成模型，用于对文档集进行降维或者潜在语义分析。

1. 算法介绍

整体说明

给定一个语料库, 该语料库由一系列文档构成。 每个文档 则由一个序列的词构成，。 语料库中的词整体构成了一个词汇表。 LDA模型需要人为指定模型的话题个数，这里用来表示。 在LDA模型中，每个文档被表示成了一个 维的话题分布，， 而每个话题 则被表示成一个 维的词分布。

LDA模型对每个文档的生成过程进行了建模。 在文档 的生成过程中，LDA首先从狄利克雷分布中采样出 一个 维的话题分布， 这里的是狄利克雷分布 的超参数。 对于文档中的每个词 ， LDA模型首先从多项分布 中采样出该词的话题， 然后再从多项分布 中采样出单词。

Gibbs Sampling

求解LDA模型的过程通常使用Gibbs Sampling方法， 通过采样出大量符合后验分布的样本, 从而对每个文档的话题分布和话题的词分布进行估计估计。 目前对LDA的Gibbs Sampling方法有大概6中，包括 Collapsed Gibbs Sampling(CGS), SparseLDA, AliasLDA, F+LDA, LightLDA和WarpLDA。 我们通过实验和分析, 认为F+LDA比较适合用于在Angel上进行LDA模型的训练。

Collapsed Gibbs Sampling

如果我们使用来表示所有词的话题， 用 来表示维度为的话题-词矩阵， 用来表示所有文档的话题分布矩阵。 那LDA模型的训练过程则是在给定观测变量和超参数的条件下， 求解隐变量的后验概率分布。 CGS通过分布之间共轭的性质将通过积分积掉，从而CGS只用迭代地采样每个 词的话题。 采样的条件概率公式如下：

F+LDA

F+LDA通过将概率公式进行了分解成两部分 和。 利用矩阵的稀疏性，从而在采样时可以只用访问非零的部分，降低了算法的复杂度。 对于另一个部分，F+LDA采用F+树来进行查找，可以将复杂度降低到O(logK)。 从而F+LDA的复杂度为， 是文档-话题矩阵中非零元素的个数。

2. 分布式训练 on Angel

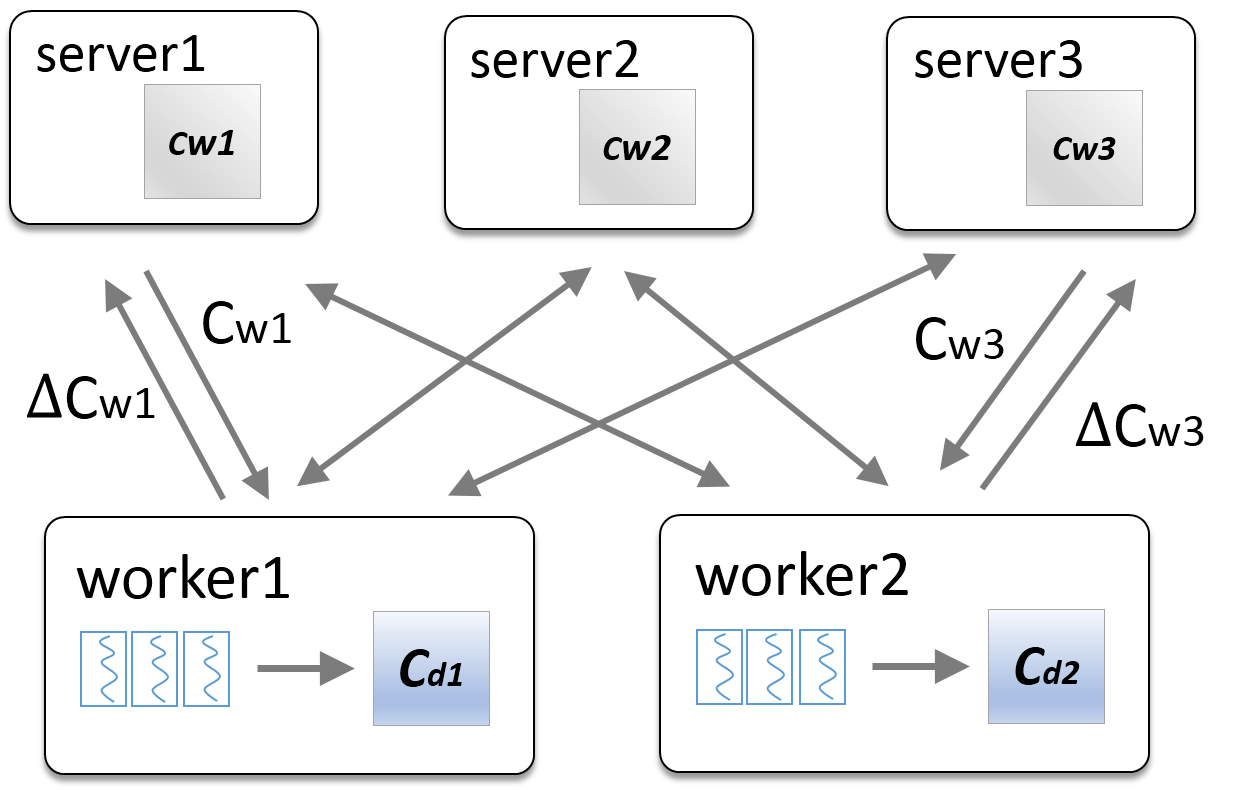
在Angel中进行LDA模型的训练，整体的框架如下图所示。 对于LDA模型中的两个较大的矩阵和 ， 我们将C_d矩阵划分到不同的worker上，将C_w矩阵划分到不同的server上。 在每一轮迭代中，worker从server上拉取C_w矩阵，从而进行话题的采样，在迭代结束时将对C_w矩阵 的更新发送回server节点。

Architecture for LDA on Angel

3. 运行 & 性能

输入格式

输入数据分为多行，每行是一个文档，每个文档由文档id和一系列的词id构成，文档id和词id之间由'\t'符合相隔，词id之间由空格隔开

	doc_id '\t' wid_0 wid_1 ... wid_n

参数

  • 数据参数
    • angel.train.data.path: 输入数据路径
    • angel.save.model.path: 模型保存路径
  • 算法参数
    • ml.epoch.num: 算法迭代次数
    • ml.lda.word.num：词个数
    • ml.lda.topic.num：话题个数
    • ml.worker.thread.num：worker内部并行度
    • ml.lda.alpha: alpha
    • ml.lda.beta: beta
    • save.doc.topic: 是否存储文档-话题矩阵
    • save.word.topic: 是否存储词-话题矩阵

性能

  • 测试数据

    • PubMED 数据集

  • 资源

    • worker：20个
    • ps：20个

  • Angel vs Spark: 迭代100次的训练时间

    • Angel：15min
    • Spark：>300min

Reference

  1. Lele Yu, Bin Cui, Ce Zhang, Yingxia Shao. LDA*: A Robust and Large-scale Topic Modeling System. VLDB, 2017