Backtracking is an algorithmic technique for solving problems incrementally by exploring all possible solutions. This topic often surfaces in coding interviews, when testing the knowledge of data structures and algorithms.
Check out our carefully selected list of basic and advanced Backtracking questions and answers to be well-prepared for your tech interviews in 2024.
👉🏼 You can also find all answers here: Devinterview.io - Backtracking
Backtracking is an algorithmic technique that uses a depth-first search approach to systematically build candidates for solutions. Each potential solution is represented as nodes in a tree structure.
If a particular pathway does not lead to a valid solution, the algorithm reverts or "backtracks" to a previous state. This strategy ensures a thorough exploration of the solution space by methodically traversing each branch of the tree.
-
Sudoku Solvers: Algorithms employ backtracking to determine valid number placements on the grid according to the game's rules.
-
Boggle Word Finders: Systems utilize backtracking to identify all valid words from a grid of letters in the Boggle game.
-
Network Router Configuration: Optimal configurations in complex networks, like routes and bandwidth allocations, are determined using backtracking.
-
University Timetable Scheduling: Backtracking aids in efficiently scheduling university courses, minimizing overlaps and optimizing resource usage.
-
Interactive Storytelling in VR: In virtual reality games, backtracking navigates and selects optimal story paths based on user decisions, ensuring a cohesive narrative.
Place
Here is the Python code:
def is_valid(board, row, col):
for i in range(row):
if board[i] in [col, col - (row - i), col + (row - i)]:
return False
return True
def place_queen(board, row):
n = len(board)
if row == n:
return True
for col in range(n):
if is_valid(board, row, col):
board[row] = col
if place_queen(board, row + 1):
return True
board[row] = -1 # Backtrack
return False
def solve_n_queens(n):
board = [-1] * n
if place_queen(board, 0):
print("Solution exists:")
print(board)
else:
print("No solution exists.")
solve_n_queens(4)The is_valid function evaluates queen placement validity, while place_queen recursively attempts to place all
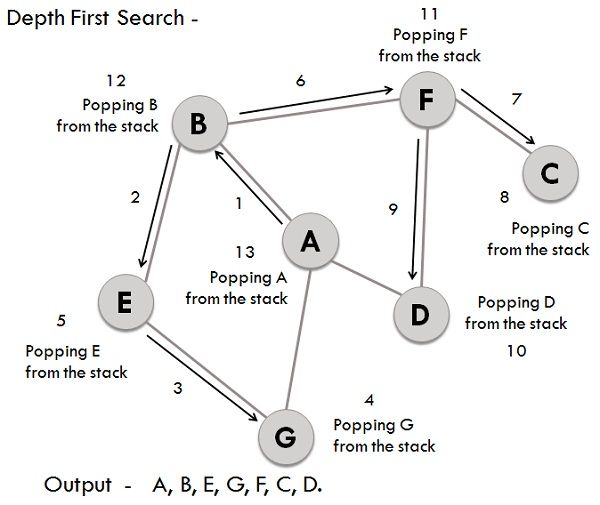
Depth-First Search (DFS) is a graph traversal algorithm that's simpler and often faster than its breadth-first counterpart (BFS). While it might not explore all vertices, DFS is still fundamental to numerous graph algorithms.
- Initialize: Select a starting vertex, mark it as visited, and put it on a stack.
- Loop: Until the stack is empty, do the following:
- Remove the top vertex from the stack.
- Explore its unvisited neighbors and add them to the stack.
- Finish: When the stack is empty, the algorithm ends, and all reachable vertices are visited.
Here is the Python code:
def dfs(graph, start):
visited = set()
stack = [start]
while stack:
vertex = stack.pop()
if vertex not in visited:
visited.add(vertex)
stack.extend(neighbor for neighbor in graph[vertex] if neighbor not in visited)
return visited
# Example graph
graph = {
'A': {'B', 'G'},
'B': {'A', 'E', 'F'},
'G': {'A'},
'E': {'B', 'G'},
'F': {'B', 'C', 'D'},
'C': {'F'},
'D': {'F'}
}
print(dfs(graph, 'A')) # Output: {'A', 'B', 'C', 'D', 'E', 'F', 'G'}Backtracking often employs recursion to explore the vast space of possible solutions. However, not all recursive algorithms involve backtracking.
Think of recursion as the mechanism that enables a function to call itself, and backtracking as a strategy where you make a choice and explore the possibilities.
-
Recursion: Utilizes a divide-and-conquer approach, breaking the main problem into smaller, self-similar subproblems. Recursive calls work towards solving these subproblems, relying on defined base cases for termination.
-
Backtracking: Operates as an advanced form of recursion by building solutions incrementally. When a partial solution is deemed unsuitable, it "backtracks" to modify previous choices, ensuring an efficient traversal through the solution space.
- Tree Traversals: Visiting all nodes in a tree, like in binary search trees.
- Divide and Conquer Algorithms: Such as merge sort or quick sort.
- Dynamic Programming: Solving problems like the coin change problem by breaking them down into smaller subproblems.
- Puzzle Solvers: Solving games like Sudoku or crossword puzzles.
- Combinatorial Problems: Generating all permutations or combinations of a set.
- Decision-making Problems: Such as the knapsack problem, where decisions are made on whether to include items.
Both Backtracking and Exhaustive Search aim to find solutions to computational problems by exploring the entire solution space.
However, backtracking is more selective, often pruning parts of the search space based on certain criteria, making it potentially more efficient than an exhaustive search which systematically checks every possible solution without exception.
- Backtracking: Incrementally creates solutions, evaluating viability at each step. Unviable paths lead the algorithm to revert and explore alternate paths.
- Exhaustive Search: Produces all possible solutions first and only then checks each one's viability.
Consider the task of finding subsets from
-
Exhaustive Search would evaluate every possible subset to find those that sum to 8. Valid subsets include
${1, 2, 5}, {1, 3, 4}, {2, 3, 4}$ among others. -
Backtracking begins with the first element and systematically adds subsequent elements. If the current subset's sum exceeds 8 or it's clear the sum cannot reach 8 with the remaining elements, it backtracks to try a different combination.
-
Exhaustive Search: Typically
$O(2^n)$ time complexity and$O(n)$ space complexity—straightforward but often less efficient. -
Backtracking: Generally offers improved time efficiency, with space complexity at
$O(n)$ .
- Password Cracking: For simple passwords, an exhaustive search or "brute force" method tries every possible combination until the correct one is found.
- Traveling Salesman Problem (Small Datasets): For a limited number of cities, an exhaustive search can determine the shortest possible route by calculating every potential
- Game Solving (Limited Possibilities): In games like Tic-Tac-Toe, exhaustive search can evaluate all possible moves to determine the best outcome.
- Sudoku Solvers: Efficiently filling out a Sudoku board by trying numbers in each cell and reverting if a contradiction is found.
- Maze Solvers: Finding a path from the start to the finish, trying different routes and backtracking when a dead-end is encountered.
- Graph Coloring: Assigning colors to vertices of a graph so that no two adjacent vertices share the same color.
👉🏼 Check out all 6 answers here: Devinterview.io - Backtracking
👉🏼 Check out all 6 answers here: Devinterview.io - Backtracking