排序算法
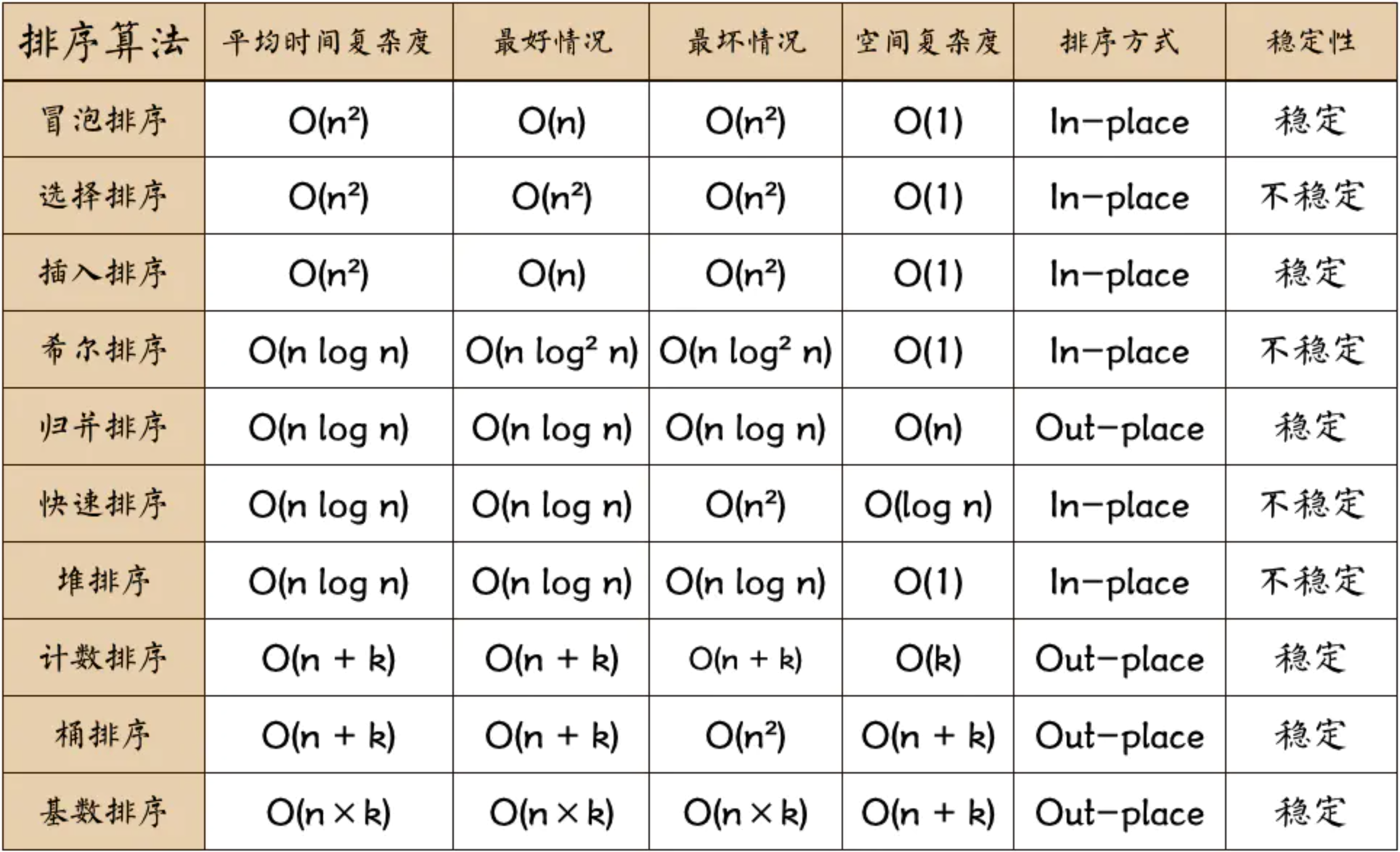
1. 冒泡排序
2. 快速排序
2.1. 挖坑法
2.2. 左右指针交换
2.3. 非递归写法
2.4. 快排常见优化
2.5. Arrays.sort()的算法
2.5.1. 对于小的数据排序使用插入排序
2.5.2. 对于中等的数据使用快排
2.5.3. 具备结构化的数组使用归并排序
3. 插入排序
4. 希尔排序
5. 简单选择排序
6. 堆排序
7. 归并排序
8. 桶排序
9. 计数排序
10. 基数排序
11. Top K 问题
11.1. 三路快排 + 二分
12. 双轴快排、二分插入排序、TimeSort(TODO)
- 交换
- 冒泡排序
- 快速排序
- 插入
- 直接插入排序
- 希尔排序
- 选择
- 简单选择排序
- 堆排序
- 归并排序
- 桶思想
- 桶排序
- 计数排序
- 基数排序
- In-place: 内部排序
- out-place: 外部排序
- 相关资料:一文搞定十大经典排序算法(Java实现)
public class Solution {
/**
* 1. 区间的元素比较,比较区间内两两之间的元素大小,进行交换
* 2. 一轮比较下来,最大的元素最大的元素被交换到最后
* 3. 再比较 n-1 的区间,以此类推。
*
* 外层循环表示当前获取第几个最大的数
* 内层循环表示进行排序的区间
* @param nums
*/
public static void sort(int[] nums) {
int len = nums.length;
for (int i = 1; i <= len; i++) {
for (int j = 0; j < len - i; j++) {
if (nums[j] > nums[j + 1]) {
int tmp = nums[j];
nums[j] = nums[j + 1];
nums[j + 1] = tmp;
}
}
}
}
}常见的左右指针交换的快拍的写法中:为什么要先从右开始查找,再从左边开始查找?
主要的区别在于最后执行基点与指针交换的操作。基点定于左侧,若先从左边开始查找,可能会导致找到一个大于的数且指针相遇了,此时与基点位置坐交换会把一个大于基点的数交换至左侧。导致区间的数存在问题。
public class Solution {
private static void sort1(int[] nums, int left, int right) {
if (left > right) {
return;
}
int i = left;
int j = right;
int tmp = nums[right];
while (i < j) {
while (i < j && nums[i] <= tmp) i++;
while (i < j && nums[j] >= tmp) j--;
swap(nums, i, j);
}
swap(nums, i, right); // 区别
sort1(nums, left, i - 1);
sort1(nums, i + 1, right);
}
}public class Solution {
public void quickSort(int[] arr, int start, int end) {
if (start > end) {
return;
}
int i = start;
int j = end;
int tmp = arr[i];
while (i < j) {
while (i < j && arr[j] >= tmp) {
j--;
}
arr[i] = arr[j];
while (i < j && arr[i] <= tmp) {
i++;
}
arr[j] = arr[i];
}
arr[i] = tmp;
quickSort(arr, start, i - 1);
quickSort(arr, i + 1, end);
}
}public class Solution {
/**
* 左右指针法
* @param arr
* @param left
* @param right
*/
public static void sort(int[] arr, int left, int right) {
if (left > right) return;
int pos = partition(arr, left, right);
sort(arr, left, pos - 1);
sort(arr, pos + 1, right);
}
public static int partition(int[] arr, int left, int right) {
int tmp = arr[left];
int i = left, j = right;
while (i < j) {
while (i < j && arr[j] >= tmp) j--;
while (i < j && arr[i] <= tmp) i++;
swap(arr, i, j);
}
swap(arr, i, left);
return i;
}
}用栈模拟递归过程
public class Solution {
public static void sort(int[] nums) {
Stack<int[]> stack = new Stack<>();
int[] sortElement = {0, nums.length - 1};
stack.push(sortElement);
while (!stack.isEmpty()) {
int[] item = stack.pop();
if (item[0] > item[1]) {
continue;
}
int partition = partition(nums, item[0], item[1]);
stack.push(new int[]{item[0], partition - 1});
stack.push(new int[]{partition + 1, item[1]});
}
}
private static int partition(int[] nums, int left, int right) {
int i = left;
int j = right;
int tmp = nums[left];
while (i < j) {
while (i < j && nums[j] >= tmp) j--;
while (i < j && nums[i] <= tmp) i++;
swap(nums, i, j);
}
swap(nums, i, left);
return i;
}
private static void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}- 随机基准。每次随机选取基准值,而不是固定选取左或右边界值。使用random
- 三数取中法。队头、队尾、队中三个数,取中间值。
- 当待排序序列的长度分割到一定大小后,使用插入排序。在子序列比较小的时候,直接插入排序性能较好,因为对于有序的序列,插排可以达到O(n)的复杂度,如果序列比较小,使用插排效率要比快排高。可以设置一个阈值n,之后使用插排。
if(right - left > 5){
int pos = partition(array, left, right);
Quicksort(array, left, pos - 1);
Quicksort(array, pos + 1, right);
}else{
insertionSort(array);
}
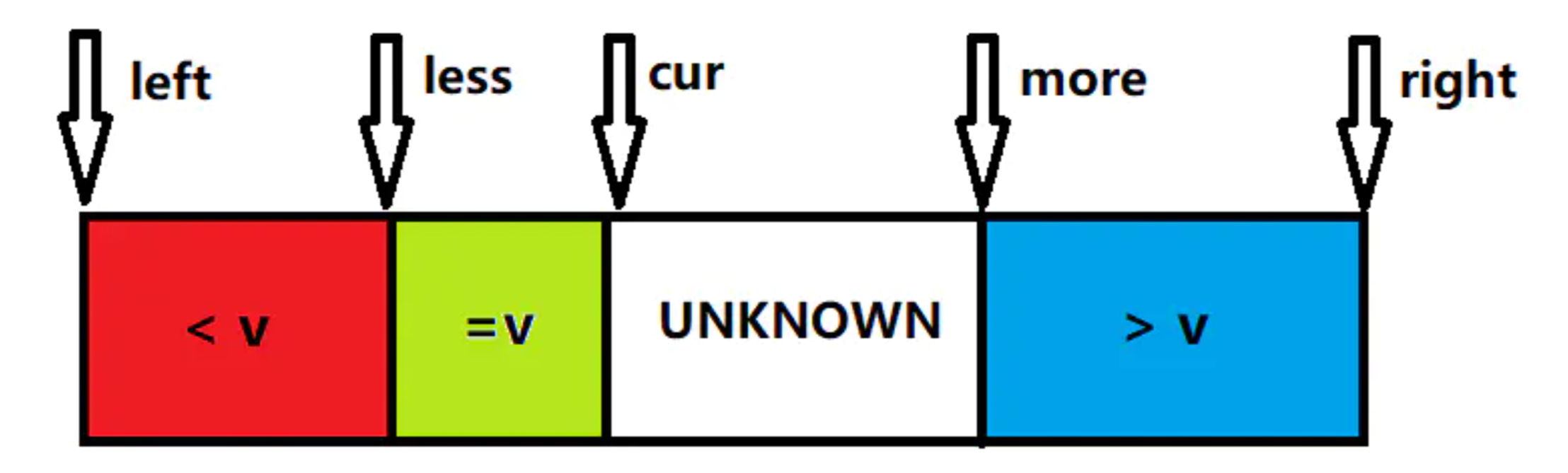
- 优化四:三路划分。如果待排序列中重复元素过多,也会大大影响排序的性能,这是因为大量相同元素参与快排时,左右序列规模相差极大,快排将退化为冒泡排序,时间复杂度接近O(n2)。
思想: 将待排序列划分为三部分:第一部分小于基准v,第二部分等于基准v,第三部分大于基准v。
这样在递归排序区间的时候,我们就不必再对第二部分元素均相等的区间进行快排了,这在待排序列存在大量相同元素的情况下能大大提高快排效率。
具体算法
public class Solution {
public static int[] partition(int[] array, int left, int right) {
int v = array[left]; //选择右边界为基准
int less = left - 1; // 最后指向 < v 部分的最后一个数
int more = right + 1; // 最后指向 > v 部分的第一个数
int cur = left;
while (cur < more) {
if (array[cur] < v) {
swap(array, ++less, cur);
cur++;
} else if (array[cur] > v) {
// 这里为什么 cur指针 cur++,因为指针从左至右开始扫描,当前不确定交换的元素是不是就大于比较值
swap(array, --more, cur);
} else {
cur++;
}
}
return new int[]{less + 1, more - 1}; //返回的是 = v 区域的左右下标
}
public static void Quicksort(int array[], int left, int right) {
if (left < right) {
int[] p = partition(array, left, right);
Quicksort(array, left, p[0] - 1); //避开重复元素区间
Quicksort(array, p[1] + 1, right);
}
}
public static void swap(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
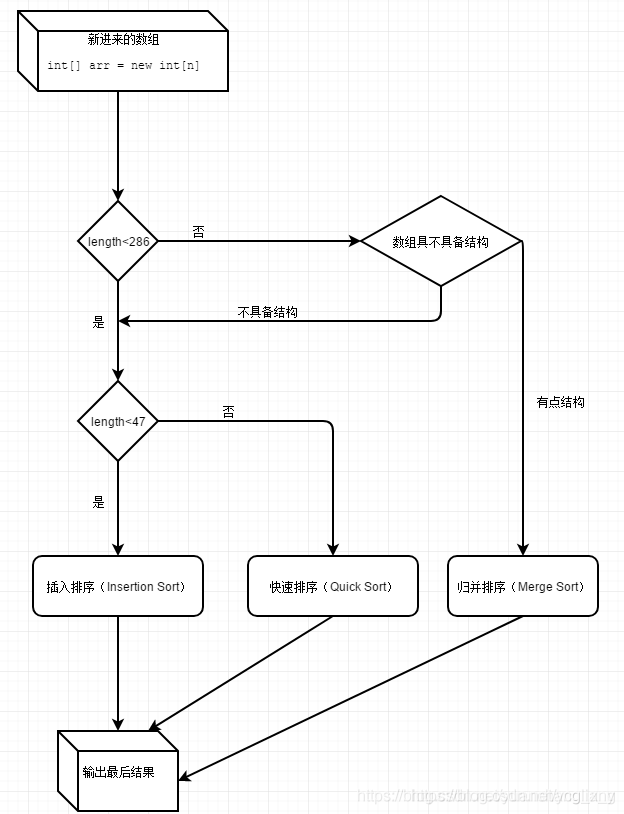
}Arrays.sort并不是单一的排序,而是插入排序,快速排序,归并排序三种排序的组合
- 数量非常小的情况下(就像上面说到的,少于47的),插入排序等可能会比快速排序更快。 所以数组少于47的会进入插入排序。
- 快排数据越无序越快(加入随机化后基本不会退化),平均常数最小,不需要额外空间,不稳定排序。
- 归排速度稳定,常数比快排略大,需要额外空间,稳定排序。
小于47个元素的数据使用插入排序
// Use insertion sort on tiny arrays
if (length < INSERTION_SORT_THRESHOLD) // 临界元素47个
插入排序:
/*
* Traditional (without sentinel) insertion sort,
* optimized for server VM, is used in case of
* the leftmost part.
*/
for (int i = left, j = i; i < right; j = ++i) {
int ai = a[i + 1];
while (ai < a[j]) {
a[j + 1] = a[j];
if (j-- == left) {
break;
}
}
a[j + 1] = ai;
}
范围大小: 47< len <286
主要流程:对数组长度乘以7,获取五个基准点,取排序后的第2和第4个基准点为双轴排序的初值,接着就是进行双轴快速排序。
for (int last; count > 1; count = last) {
for (int k = (last = 0) + 2; k <= count; k += 2) {
int hi = run[k], mi = run[k - 1];
for (int i = run[k - 2], p = i, q = mi; i < hi; ++i) {
if (q >= hi || p < mi && a[p + ao] <= a[q + ao]) {
b[i + bo] = a[p++ + ao];
} else {
b[i + bo] = a[q++ + ao];
}
}
run[++last] = hi;
}
if ((count & 1) != 0) {
for (int i = right, lo = run[count - 1]; --i >= lo;
b[i + bo] = a[i + ao]
);
run[++last] = right;
}
int[] t = a; a = b; b = t;
int o = ao; ao = bo; bo = o;
}
public class Solution {
/**
* 插入排序
* 每次插入新元素到整齐的区间
* @param arr
*/
public static void sort(int[] arr) {
int len = arr.length;
for (int i = 1; i < len; i++) {
for (int j = i; j > 0; j--) {
if (arr[j] < arr[j - 1]) {
int tmp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = tmp;
}
}
/* for (int j = i; j >0 && arr[j] <= arr[j-1]; j--) {
int tmp = arr[j];
arr[j] = arr[j-1];
arr[j-1] = tmp;
} */
}
}
}public class Solution {
public static void sort(int[] arr) {
int gap = arr.length;
while (gap > 1) {
gap = gap / 2;
for (int i = 0; i < gap; i++) {
for (int j = i + gap; j < arr.length; j += gap) {
// 在shell gap 间隔的区间进行交换排序
int k = j - gap;
while (k >= 0 && arr[k] > arr[k + gap]) {
int tmp = arr[k + gap];
arr[k + gap] = arr[k];
arr[k] = tmp;
}
//这是使用覆盖性质的排序,减少了交换次数。
/* int tmp = nums[j], k=j-gap;
while (k>=0 && nums[k] > tmp) {
nums[k+gap] = nums[k];
k-=gap;
}
nums[k+gap] = tmp;
*/
}
}
}
}
}public class Solution {
/**
* 选择一个最小的元素交换至第一位
* 选择一个次小的元素交换至第二位
* 以此类推
* @param arr
*/
public static void sort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
int min = i;
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) {
min = j;
}
}
if (min != i) {
int tmp = arr[i];
arr[i] = arr[min];
arr[min] = tmp;
}
}
}
}public class Solution {
public static void sort(int[] arr) {
//1.构建大顶堆
for (int i = arr.length / 2 - 1; i >= 0; i--) {
//从第一个非叶子结点从下至上,从右至左调整结构
adjustHeap(arr, i, arr.length);
}
//2.调整堆结构+交换堆顶元素与末尾元素
for (int j = arr.length - 1; j > 0; j--) {
swap(arr, 0, j);//将堆顶元素与末尾元素进行交换
adjustHeap(arr, 0, j);//重新对堆进行调整
}
}
/**
* 调整大顶堆(仅是调整过程,建立在大顶堆已构建的基础上)
*
* @param arr
* @param i
* @param length
*/
public static void adjustHeap(int[] arr, int i, int length) {
int temp = arr[i];//先取出当前元素i
for (int k = i * 2 + 1; k < length; k = k * 2 + 1) {//从i结点的左子结点开始,也就是2i+1处开始
if (k + 1 < length && arr[k] < arr[k + 1]) {//如果左子结点小于右子结点,k指向右子结点
k++;
}
if (arr[k] > temp) {//如果子节点大于父节点,将子节点值赋给父节点(不用进行交换)
arr[i] = arr[k];
i = k;
} else {
break;
}
}
arr[i] = temp;//将temp值放到最终的位置
}
/**
* 交换元素
*
* @param arr
* @param a
* @param b
*/
public static void swap(int[] arr, int a, int b) {
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
}public class Solution {
/**
* 递归归并排序
* @param nums
* @param start
* @param end
* @return
*/
public static int[] sort(int[] nums, int start, int end) {
if (start == end) {
return new int[]{nums[start]};
}
int mid = start + (end - start) / 2;
int[] left = sort(nums, start, mid);
int[] right = sort(nums, mid + 1, end);
int[] result = new int[left.length + right.length];
int index = 0, i = 0, j = 0;
while (index < result.length && i < left.length && j < right.length) {
result[index++] = left[i] < right[j] ? left[i++] : right[j++];
}
while (i < left.length) {
result[index++] = left[i++];
}
while (j < right.length) {
result[index++] = right[j++];
}
return result;
}
/**
* 非递归归并
* @param array
* @return
*/
public static int[] sort2(int[] array) {
int len = array.length;
int[] result = new int[len];
int block, start;
for (block = 1; block < len * 2; block *= 2) {
for (start = 0; start < len; start += block * 2) {
int low = start;
int mid = (start + block) < len ? (start + block) : len;
int end = (start + block * 2) < len ? (start + block * 2) : len;
int start1 = low, end1 = mid;
int start2 = mid, end2 = end;
while (start1 < end1 && start2 < end2) {
result[low++] = array[start1] < array[start2] ? array[start1++] : array[start2++];
}
while (start1 < end1) {
result[low++] = array[start1++];
}
while (start2 < end2) {
result[low++] = array[start2++];
}
}
int[] temp = array;
array = result;
result = temp;
}
result = array;
return result;
}
}public class Solution {
/**
* 桶排序
* 1. 获取最大最小树,桶的空间
* 2. num[i] -min 定位桶索引,添加当前树到桶中。
* 3. 使用索引扫描每个桶位,更新到排序数组中
* @param nums
*/
public static void sort(int[] nums) {
int len = nums.length;
int min = Integer.MAX_VALUE;
int max = Integer.MIN_VALUE;
for (int num : nums) {
min = Math.min(num, min);
max = Math.max(num, max);
}
ArrayList<Integer>[] buckets = new ArrayList[max - min + 1];
for (int i = 0; i < buckets.length; i++) {
buckets[i] = new ArrayList<>();
}
for (int i = 0; i < len; i++) {
buckets[nums[i] - min].add(nums[i]);
}
for (int i = 0, j = 0; i < buckets.length; i++) {
List<Integer> curList = buckets[i];
int index = 0;
while (!curList.isEmpty() && index < curList.size()) {
nums[j++] = curList.get(index++);
}
}
}
}public class Solution {
/**
* 不稳定排序版本
* @param array
* @return
*/
public static int[] sort(int[] array) {
int min = Integer.MAX_VALUE, max = Integer.MIN_VALUE;
for (int i = 0; i < array.length; i++) {
if (array[i] > max) {
max = array[i];
}
if (array[i] < min) {
min = array[i];
}
}
int[] countArray = new int[max - min + 1];
for (int i = 0; i < array.length; i++) {
countArray[array[i] - min]++;
}
int[] sortArray = new int[array.length];
for (int j = 0, i = 0; j < countArray.length; j++) {
while (countArray[j] > 0) {
sortArray[i++] = j + min;
countArray[j]--;
}
}
return sortArray;
}
/**
* 优化版计数排序
*
* @param array
* @return
*/
public static int[] countSort(int[] array) {
//1.得到数列的最大值与最小值,并算出差值d
int max = array[0];
int min = array[0];
for (int i = 1; i < array.length; i++) {
if (array[i] > max) {
max = array[i];
}
if (array[i] < min) {
min = array[i];
}
}
int d = max - min;
//2.创建统计数组并计算统计对应元素个数
int[] countArray = new int[d + 1];
for (int i = 0; i < array.length; i++) {
countArray[array[i] - min]++;
}
//3.统计数组变形,后面的元素等于前面的元素之和
int sum = 0;
for (int i = 0; i < countArray.length; i++) {
sum += countArray[i];
countArray[i] = sum;
}
//4.倒序遍历原始数组,从统计数组找到正确位置,输出到结果数组
int[] sortedArray = new int[array.length];
for (int i = array.length - 1; i > 0; i--) {
sortedArray[countArray[array[i] - min] - 1] = array[i];
// -1 表示后来的元素的位置应向前移动
countArray[array[i] - min]--;
}
return sortedArray;
}
}public class Solution {
/**
* 基数排序
* 循环:
* 1. 获取每个数的第i个位置的基数,放到桶中
* 2. 遍历桶元素替换到排序数组中
* 3. 递归循环直至最高位的基数
* @param nums
*/
public static void sort(int[] nums) {
List<Integer>[] buckets = new ArrayList[10];
for (int i = 0; i < buckets.length; i++) {
buckets[i] = new ArrayList<>();
}
int max = Integer.MIN_VALUE;
for (int num : nums) {
max = Math.max(max, num);
}
int maxLen = String.valueOf(max).length();
int mod = 10, div = 1;
for (int i = 1; i <= maxLen; i++, mod *= 10, div *= 10) {
for (int num : nums) {
// 求当前数在位置i上的基数
int index = (num % mod) / div;
buckets[index].add(num);
}
int index = 0;
for (List<Integer> curList : buckets) {
int curIndex = 0;
while (curIndex < curList.size()) {
nums[index++] = curList.get(curIndex++);
}
curList.clear();
}
}
}
}public class Solution {
public static void main(String[] args) {
int[] array = {12, 3, 12, 3, 1, 12, 12, 12, 1, 5, 7, 23, 123, 45, 2, 15, 12};
List<Integer> topK = getTopK(array, 5);
System.out.println(Arrays.toString(topK.toArray()));
}
public static List<Integer> getTopK(int[] nums, int target) {
List<Integer> list = new ArrayList<>();
int start = 0, end = nums.length - 1;
int point = -1;
while (start < end) {
int[] partition = partition(nums, start, end);
if (partition[1] < target) {
start = partition[1];
} else if (partition[0] > target) {
end = partition[0];
} else {
point = target;
break;
}
}
for (int i = 0; i < point; i++) {
list.add(nums[i]);
}
return list;
}
public static int[] partition(int[] nums, int start, int end) {
int i = start - 1, j = end + 1;
int index = start + 1;
int pivot = nums[start];
while (index < j) {
if (nums[index] < pivot) {
swap(nums, index, ++i);
index++;
} else if (nums[index] > pivot) {
swap(nums, index, --j);
} else {
index++;
}
}
return new int[]{i, j};
}
public static void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}- 相关资料:面试官最喜爱的TopK问题算法详解
TimeSort: 一个稳定的具有自适应性的MergeSort算法