| title | tags | ||||||
|---|---|---|---|---|---|---|---|
45. NP完全性 |
|
在上一讲中,我们介绍了 P 类和 NP 类。这一讲,我们将深入探讨 NP 完全性的概念,这是复杂性理论中的一个核心主题,也是理解许多密码学和零知识证明系统的基础。
在讨论 NP 完全性之前,我们需要先理解归约(Reduction)的概念。归约是将某个计算问题变换为另一个问题的过程,规约在复杂性理论中起着重要的作用,它允许我们比较问题的相对难度。
如果问题 A 可以转化为问题 B,那么我们就可以用 B 的答案去解决 A,也就是说 B 至少和 A 一样难。换句话说,如果我们能解决问题 B,就能解决问题 A。
根据可计算性理论,如果问题 A 可规约到问题 B,且问题 B 是可判定的,则问题 A 也是可判定的。等价地,如果问题 A 不可判定,且可规约到问题 B,则问题 B 也是不可判定的。
映射归约(Mapping Reduction)是最基本的归约类型。
定义:给定两个语言
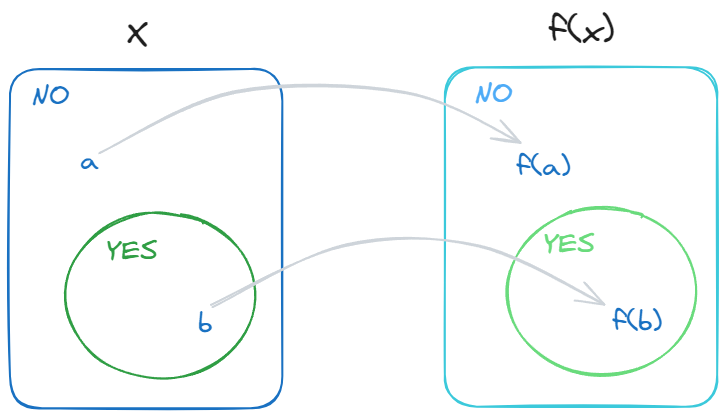
映射规约指的是,存在一个可计算函数(规约),它将问题 A 的实例转换成问题 B 的实例。如果有了这样的一个可计算函数,就能用问题 B 的解决方法来解决问题 A。
映射归约展示了如何利用一个映射将一个问题转化为另一个问题。
多项式时间归约(Polynomial-time Reduction)是映射归约的一个更强版本,它要求归约过程必须在多项式时间内完成。
定义:如果存在一个多项式时间算法
如同一般的映射规约一样,A 到 B 的多项式时间规约提供了一种方法,把 A 的成员资格判定转化为 B 的成员资格判定,只是这种转化是在多项式时间内有效完成的。为了判定是否
如果
我们以离散对数问题(DLP)和计算 Diffie-Hellman 问题(CDH)为例,其中:
-
DLP:给定循环群
$G$ 、生成元$g$ 和元素$y \in G$ ,找到整数$x$ 使得$g^x = y$ 。 -
CDH:给定循环群
$G$ 、生成元$g$ 以及$g^a$ 和$g^b$ (其中$a$ 和$b$ 未知),计算$g^{ab}$ 。
这两个密码学常用难题均为NP类,没有多项式时间的有效解法。那它们之间是否存在归约关系呢?
答案是有的,如果能解决 DLP,就能轻松的解决CDH问题:给定
NP 类包含非常多的算法,那么人们如何证明 P = NP 呢?1970 年左右,研究者 Cook 和 Levin 发现 NP 中某些问题的复杂性可以和整个类的复杂性产生关联:如果这些问题中的任何一个多项式时间算法,那么所有 NP 问题都是多项式时间可解的,即 P = NP。这类问题被称为 NP 完全问题(NP-complete),是 NP 类中最难的问题。
如果语言
-
$B \in \text{NP}$ ,并且 - 对于每个
$A \in \text{NP}$ ,有$A \leq_p B$ . 即 NP 中的每个$A$ 都多项式时间可规约到$B$ 。
若
也就是说,若
即所有 NP 问题都可以在多项式时间归约到 NP 完全问题。因此,如果找到任何一个 NP 完全问题的多项式时间算法,那么所有 NP 问题都可以在多项式时间内解决 (P = NP)。
如果
SAT(布尔可满足性问题)是第一个被证明为 NP 完全的问题,在复杂性理论和实际应用中都有重要地位。
我们先复习一下布尔变量,布尔运算和布尔公式。
布尔变量指取值为 TRUE 或 FALSE 的变量,通常我们用 1 表示 TRUE,用 0 表示 FALSE。
布尔运算包含AND,OR,NOT(与、或、非运算),分别用符号
$0 \wedge 0 = 0$ $0 \wedge 1 = 0$ $1 \wedge 0 = 0$ $1 \wedge 1 = 1$ $0 \vee 0 = 0$ $0 \vee 1 = 1$ $1 \vee 0 = 1$ $1 \vee 1 = 1$ $\bar{0} = 1$ $\bar{1} = 0$
布尔公式是包含布尔变量和运算的表达式,例如
如果存在变量
SAT 问题:给定一个布尔公式
对于
赋值
Cook-Levin 定理是复杂性理论中的一个里程碑,它证明了 SAT 问题不仅属于 NP,而且是 NP 完全的,即每个 NP 语言
- 它建立了第一个 NP 完全性问题,即 SAT。
- 它建立了一个模板,可以用来证明其他问题的 NP 完全性。( 对于某问题
$A$ ,证明$\text{SAT} \leq_p A$ ,$A$ 属于 NP,则$A$ 是 NP 完全的 )
Cook-Levin 定理的证明思路是将任意 NP 问题的验证过程编码为一个布尔公式,证明过程超出本教程范围,请大家自行查阅。
下图展示了一个基于Cook-Levin 定理的,由 SAT 问题到三色图着色问题(Graph Coloring Problem)的简单映射:
这一讲,我们介绍了归约和 NP 完全性。归约可以让我们比较不同问题的相对难度。NP 完全性是 NP 中最难的一类问题,所有 NP 问题都可以归约到它们。SAT 问题是第一个被证明为 NP 完全的问题。