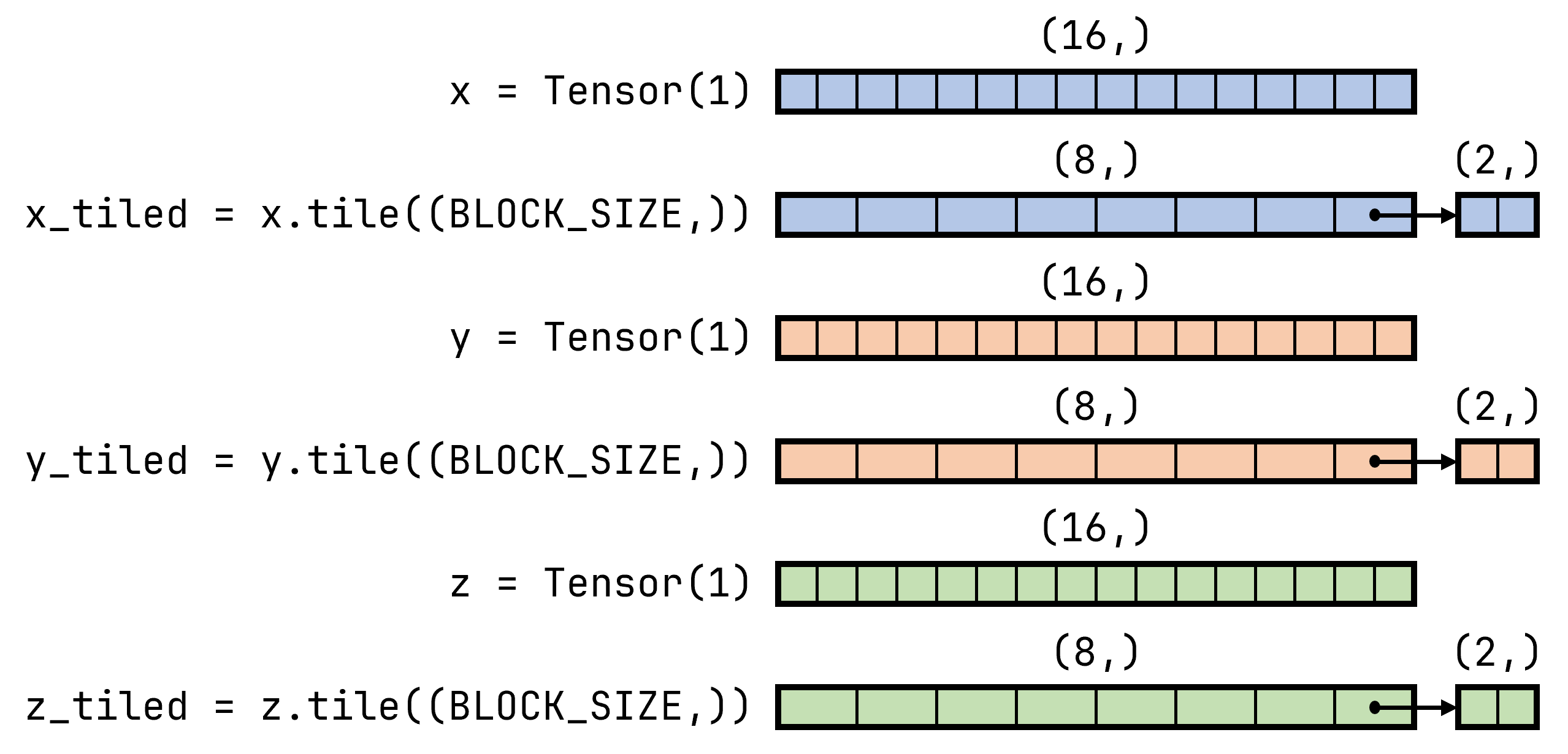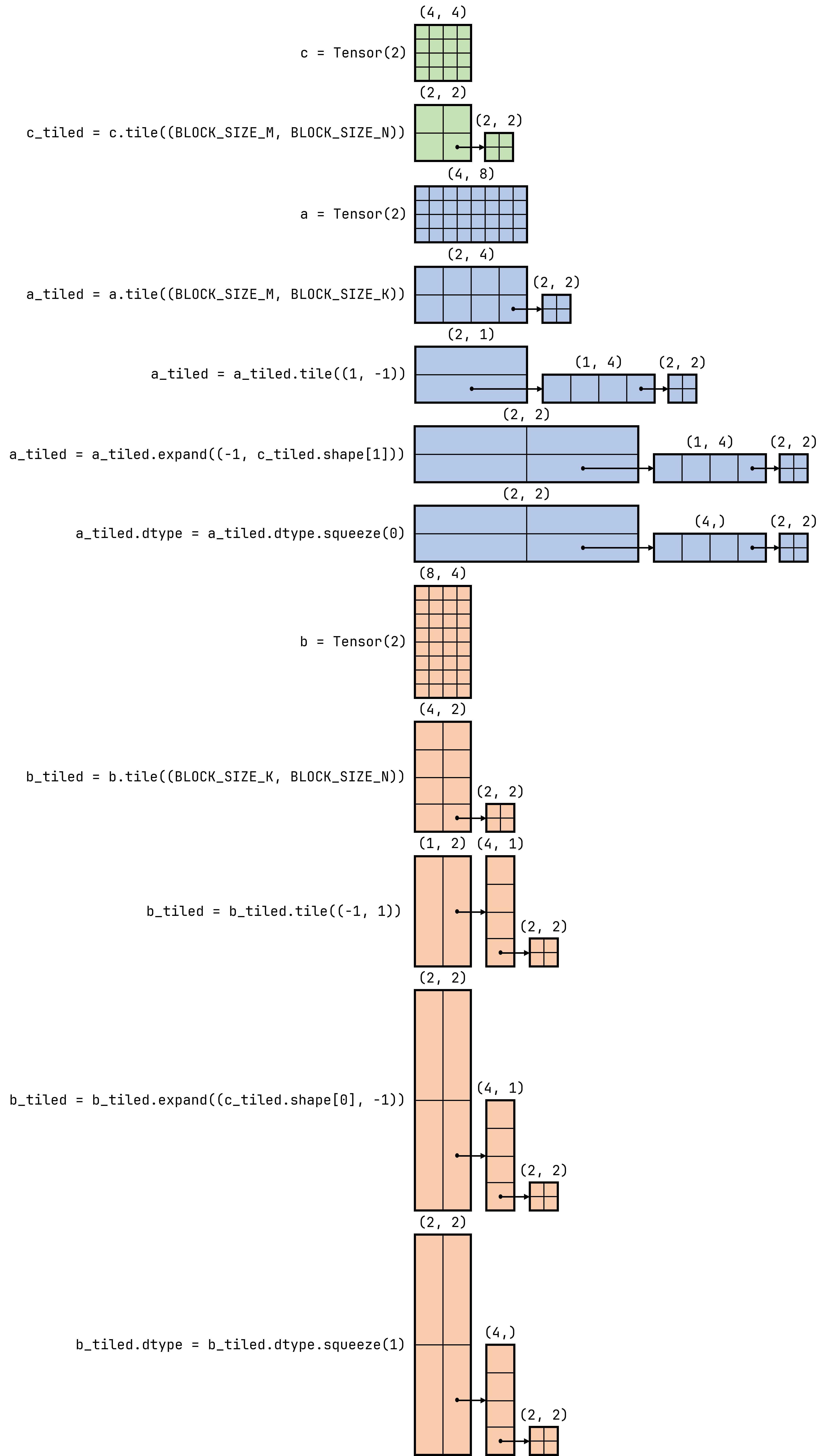A domain-specific language (DSL) based on Triton but providing higher-level abstractions.
Other language versions: English, 简体中文.
We can use pip to install ninetoothed.
pip install ninetoothedAfter successfully running the above command, ninetoothed will be installed. However, to fully utilize its capabilities, you also need to install a deep learning framework supported by ninetoothed. For trial purposes, we recommend installing torch.
Currently, we can use the Tensor and Symbol classes in the ninetoothed package to perform meta-operations like tile and expand to easily construct kernel functions. Below, we will use these features to create vector addition and matrix multiplication kernel functions.
BLOCK_SIZE = Symbol("BLOCK_SIZE", meta=True)
@ninetoothed.jit
def add_kernel(
x: Tensor(1).tile((BLOCK_SIZE,)),
y: Tensor(1).tile((BLOCK_SIZE,)),
z: Tensor(1).tile((BLOCK_SIZE,)),
):
z = x + yIn this code, we first define BLOCK_SIZE, which is a Symbol. You can think of "BLOCK_SIZE" as its name. We see that meta is set to True, indicating to the compiler that it is a meta-parameter and its value can be determined by the compiler. The Tensor(1) constructs a one-dimensional tensor (vector), and Tensor(1).tile((BLOCK_SIZE,)) means we want to create a vector and divide it into blocks of size BLOCK_SIZE. Suppose the size of this vector is 8192 and BLOCK_SIZE is 1024, then the vector will be divided into 8 blocks, each of size 1024.
By using type annotations, we tell the compiler that we will have three tensor parameters, which will be divided into blocks, and x, y, and z are these blocks. It's important to understand that x, y, and z are the blocks, not the tensors themselves. In the function body, x, y, and z are also the blocks. The rest is straightforward (only one line z = x + y left, haha), we add each block of x and y and store it in z. Since each block of the parameter tensors undergoes this operation, the addition is completed for the whole tensors as well.
BLOCK_SIZE_M = Symbol("BLOCK_SIZE_M", meta=True)
BLOCK_SIZE_N = Symbol("BLOCK_SIZE_N", meta=True)
BLOCK_SIZE_K = Symbol("BLOCK_SIZE_K", meta=True)
a_tiled = Tensor(2).tile((BLOCK_SIZE_M, BLOCK_SIZE_K)).tile((1, -1))
b_tiled = Tensor(2).tile((BLOCK_SIZE_K, BLOCK_SIZE_N)).tile((-1, 1))
c_tiled = Tensor(2).tile((BLOCK_SIZE_M, BLOCK_SIZE_N))
a_tiled = a_tiled.expand((-1, c_tiled.shape[1]))
b_tiled = b_tiled.expand((c_tiled.shape[0], -1))
a_tiled.dtype = a_tiled.dtype.squeeze(0)
b_tiled.dtype = b_tiled.dtype.squeeze(1)
@ninetoothed.jit
def matmul_kernel(a: a_tiled, b: b_tiled, c: c_tiled):
accumulator = ninetoothed.language.zeros(
c.shape, dtype=ninetoothed.language.float32
)
for k in range(a.shape[0]):
accumulator += ninetoothed.language.dot(a[k], b[k])
c = accumulator.to(ninetoothed.language.float16)For matrix multiplication, we also have three tensor parameters, but the tiling method is more complex than vector addition. We denote the three matrices as (BLOCK_SIZE_M, BLOCK_SIZE_N) by rows and columns. Once each block computes its result, the entire BLOCK_SIZE_K. This way, we can divide (BLOCK_SIZE_M, BLOCK_SIZE_K) and (BLOCK_SIZE_K, BLOCK_SIZE_N). However, for matrix multiplication, tile expand comes in. We expand the row blocks of (1, ...) and (..., 1). This means that if no other operations are performed, the way we access row blocks and column blocks would have to be a[0, k] and b[k, 0]. If we want to use a to find the range of k, we would need to use a.shape[1], but we know that dimensions of size 1 can actually be removed completely. This is why we added two lines of squeeze. The dtype refers to the data type, which in PyTorch can generally be some integer or floating-point type, such as torch.float32. However, since meta-operations like tile can be performed in NineToothed, dtype can also be a Tensor. In other words, there is a concept of "tensors that store tensors" in NineToothed. In summary, these two lines perform operations on the tensors stored in the outmost tensor, removing the dimensions of size 1. This way, when we access the row and column blocks, we can use a[k] and b[k], and when finding the range of k, we can use a.shape[0].
With tiling done, the rest is simple. In the function body, we define an accumulator to accumulate intermediate results. We then iterate through the corresponding row blocks of accumulator. Finally, we place the accumulator in the corresponding block of
This project is distributed under the Apache-2.0 license. See the included LICENSE file for details.