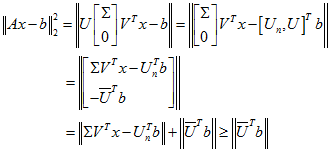README.md

线性优化（Linear Optimization)

标签（空格分隔）： SLAM Optimize

---

[toc]

1. 概述

线性方程求解是非线性优化的基础。 本节主要介绍如何求解线性方程组，从而引出常见的矩阵分解方法如SVD，QR，LU，Cholesky等。

2. 如何学习本课程？

首先我们建议先跟着本课程的内容完成学习并了解基本概念和操作流程，同时可以查找相关资料进行详细了解。

课程目标：学会求解齐次和非齐次线性方程组，并进行实践

3. 课程内容

3.1. 非齐次线性方程组和最小二乘问题

对于一般线性方程组： $$Ax=b$$

其中Ａ为ｍ＊ｎ维矩阵，ｂ是非０向量，即ｍ个方程求解ｎ个未知数，一般来说可分为以下三种情况：

1. $m=n$且A为非奇异，则有唯一解，$x=A^{-1}b$
2. $m>n$，约束的个数大于未知数的个数，称为超定问题（overdetermined）
3. $m<n$，负定/欠定问题（underdetermined）

通常我们遇到的都是超定问题，此时$Ax=b$的解是不存在的，从而转向解最小二乘问题： $$J(x)=||Ax-b||_2^2$$ 求解： $$min J(x)$$

由于这里J(x)为凸函数，因此其有唯一最优解，且满足一阶导数为0，得到： $$A^{T}Ax-A^{T}b=0$$ 称之为正规方程．由此可得方程的解为： $$x=(A^TA)^{-1}A^Tb$$ 其中对于$(A^TA)^{-1}A^T$我们将之定义为伪逆$A^{-1}$: $$A^{-1}:=(A^TA)^{-1}A^T$$

直接根据定义求解伪逆效率比较低，我们将在下面介绍如何求解伪逆和以上线性方程组．

3.2. SVD分解（奇异值分解）

3.2.1. 定义

任意一个$mn$维的矩阵A可以分解为: $$A=USV^{T}$$,其中 $U,V$为酉矩阵(正交单位阵)， $S$是$mn$维的对角矩阵，其对角线元素$\sigma$为$A$的从大到小排序的非负奇异值。

其中$S$中的奇异值$\sigma$可看作$AA^T$中特征值$\lambda$的平方根.

SVD分解十分强大且适用，因为任意一个矩阵都可以实现SVD分解，相比与SVD分解，特征值分解只能应用于方阵。

3.2.2. 矩阵压缩

在矩阵Ｓ中也是从大到小排列，而且$\sigma$的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说，我们也可以用前r大的奇异值来近似描述矩阵，这里定义一下部分奇异值分解： $$A_{mn} \approx U_{mr}S_{rr}V_{rn}^T$$ 三个矩阵相乘的结果将会是一个接近于A的矩阵，在这儿，r越接近于n，则相乘的结果越接近于A。

3.2.3. SVD分解求伪逆

对于伪逆通过定义： $$A^{-1}=(A^TA)^{-1}A^T$$ $$=(VS^TU^TUSV^T)^{-1}A^T$$ $$=VS^{-1}S^{-T}V^TVS^TU^T$$ $$=VS^{-1}U^T$$

3.2.4. 奇异值分解与线性最小二乘问题

设$A \in R^{m*n}$列满秩，$A=U\begin{bmatrix} \Sigma \ 0 \end{bmatrix}V^T$ 是A的奇异值分解。

令$U_n$为U的前n列矩阵，即$U=[U_n,U]^T$ ，则：

等号当且仅当$\Sigma V^Tx-U_n^Tb=0$时成立，所以： $$x=V\Sigma^{-1}U_n^Tb=VS^{-1}U^Tb$$ 这就是线性最小二乘问题的解,这与前面的伪逆表达式吻合。

3.3. 其他矩阵分解

为了提高运算速度，节约存储空间，通常会采用矩阵分解的方案，常见的矩阵分解有LU分解、QR分解、Cholesky分解、Schur分解、奇异分解等。这里简单介绍几种（按照使用要求从严格到松散排列）：

矩阵分解名称	使用条件	方法特点
Cholesky分解	对称正定	解唯一，非齐次线性方程求解，在高斯牛顿，LM等二阶非线性优化算法中广泛使用
Eigen分解	可对角化方阵	在齐次线性方程组求解，矩阵求逆中应用广泛
LU分解	可逆方阵	矩阵求逆，非齐次线性方程求解
Schur分解	方阵	可用于求解Eigen分解
QR分解	方阵	矩阵求逆，非齐次线性方程求解，可进一步进行Schur分解
SVD分解	其他	非齐次方程求解,矩阵压缩等

3.3.1. QR分解

对于方阵$A_{nn}$: $$A_{nn}=QR$$ 其中， Q：正交矩阵 R: 上三角矩阵 利用QR分解可求逆： $$A^{-1}=R^{-1}Q^T$$

利用QR分解可求解非齐次线性方程组：先求$Rx$,再求$x$．

3.3.2. LU分解

在线性代数中， LU分解(LU Decomposition)是矩阵分解的一种，可以将一个矩阵分解为一个单位下三角矩阵和一个上三角矩阵的乘积（有时是它们和一个置换矩阵的乘积）。LU分解主要应用在数值分析中，用来解线性方程、求反矩阵或计算行列式。

对于非奇异方阵A，LU分解总可进行： $$A_{n*n}=LU$$ L:单位下三角矩阵 U:上三角矩阵

当系数矩阵A完成了LU分解后，方程组Ax = b就可以化为L(Ux) = b，等价于求解两个方程组Ly = b和Ux = y,由此可以快速求解线性方程组

3.3.3. Cholesky分解

对于对称正定阵： $$A_{n*n}=LL^T$$ $L$:下三角矩阵 $L^T$:上三角矩阵

如果任何非零向量z,都有$z^{T}Az>0$,则X为正定矩阵。充要条件是A的特征值全为正。

同LU分解，Cholesky分解可以用来快速求解线性方程组,同样地也在非线性优化里占据非常重要的地位．

3.3.4. Eigen分解

对于可对角化方阵： $$A_{n*n}=Q\Lambda Q^{-1}$$ 其中$\Lambda$为特征值$\lambda$组成的对角阵，Q为对应的特征向量.

任意n阶方阵A可以分解为AV=VD，其中D为特征值对角阵，V是特征向量矩阵。

3.3.5. Schur分解

对于方阵有： $$A_{n*n}=QUQ^{-1}$$

其中 Q为酉矩阵， U为上三角矩阵

其分解结果不唯一，由于Q为酉矩阵，U的特征值与Ａ一致，又因为Ａ为上三角矩阵，因此特征值都分布在Ｕ的对角线上．

3.4. 齐次线性方程组和最小二乘问题

当式子$Ax=b$中的ｂ为０时，齐次线性方程组$Ax=0$的求解可转化为： $$min||Ax|| $$ $$st. ||x||=1$$

此时，最小二乘解为$A^{T}A$最小特征值对应的特征向量。

感性认识：如果$x$是$A^{T}A$的特征向量，则目标函数:$$||Ax||=x^{T}(A^{T}A)x=\lambda^{2}||x||$$

求解方案：

$eig(A^{T}A)=[V,D]$，V为特征向量阵，找最小特征值对应的V中的特征向量。 $svd(A)=[U,S,V]$，前面我们知道U是$AA^{T}$的特征值,V是$A^{T}A$的特征值,找S中最小奇异值对应的V的右奇异向量即可。

3.5. 非齐次线性方程组求解方法选择

以上介绍了很多种非齐次线性方程组的求法，那一般来说如何根据Ａ的特点选择用哪一种分解方式呢？以下表格可以作为一定的参考，优先选择靠上面的方式： |Ａ矩阵情形|方法|运算复杂度|方法特点| |-----|-------|------| |对称正定|Cholesky分解||在高斯牛顿，LM等二阶非线性优化算法中广泛使用| |可逆方阵|LU分解|| |方阵|QR分解||| |其他|SVD分解|||

3.6. 示例

4. 作业

参考GSLAM中的GSLAM/plugins/estimator_opencv/EstimatorOpenCV.cpp文件，使用Eigen库实现函数findSIM3和findPlane．