이 저장소는 TypeScript를 사용하는 함수형 프로그래밍 개념과 fp-ts 생태계의 라이브러리를 소개합니다.

이 사본은 Giulio Canti의 "Introduction to Functional Programming (Italian)"의 번역본입니다. 저자는 함수형 프로그래밍에 대한 강의와 워크숍을 위해 원본을 참고 자료로 사용합니다.

사본의 목적은 개념이나 구조를 변경하지 않고 자료를 확장하는 것입니다. 목표에 대한 자세한 내용은 CONTRIBUTING 파일을 참조하십시오.

설정하기

git clone https://github.com/gcanti/functional-programming.git
cd functional-programming
npm i

함수형 프로그래밍이란

함수형 프로그래밍은 순수 함수(수학 함수)를 이용해 프로그래밍하는 것입니다.

인터넷에서 검색하면 다음 정의를 찾을 수 있습니다.

(순수) 함수는 같은 입력이 주어지면 부작용 없이 항상 같은 출력을 반환하는 프로시저입니다.

"부작용"이라는 단어는 아직 구체적인 의미가 없습니다(앞으로 공식적인 정의를 제공하는 방법을 살펴보겠습니다). 중요한 것은 일종의 직관을 갖고 파일을 열거나 데이터베이스에 쓰는 것에 대해 생각하는 것입니다.

당분간 우리는 부작용이 값을 반환하는 것 외에 함수가 하는 모든 것이라고 스스로 제한할 수 있습니다.

순수 함수만 사용하는 프로그램의 구조는 무엇일까요?

함수형 프로그램은 파이프라인처럼 작성되는 경향이 있습니다.

const program = pipe(
  input,
  f1, // 순수 함수
  f2, // 순수 함수
  f3, // 순수 함수
  ...
)

여기서 일어나는 일은 input이 첫 번째 함수 f1에 전달되고 두 번째 함수 f2에 전달되는 값을 반환하고, 두 번째 함수에서 세 번째 함수 f3에 인자로 전달되는 값을 반환하는 것 등이 있습니다.

데모

00_pipe_and_flow.ts

함수형 프로그래밍이 해당 스타일로 코드를 구조화하는 도구를 제공하는 방법을 살펴보겠습니다.

함수형 프로그래밍이 무엇인지 이해하는 것 외에도 함수형 프로그래밍의 목적을 이해하는 것도 중요합니다.

함수형 프로그래밍의 목표는 형식적인 모델을 사용해 시스템의 복잡성을 줄이고 코드의 속성과 리팩토링을 용이하게 하는 것에 중점을 두는 것입니다.

함수형 프로그래밍은 사람들에게 프로그램 구성 뒤에 있는 수학을 가르치는 데 도움이 될 것입니다.

• 합성 가능한 코드를 작성하는 방법
• 부작용에 대해 추론하는 방법
• 일관되고 일반적이며 덜 임시적인 API를 작성하는 방법

코드의 속성에 중점을 둔다는 것은 무엇을 의미할까요? 예시를 들어 보겠습니다.

예시

Array의 map 메소드가 for 루프보다 "더 함수적"이라고 말할 수 있는 이유는 무엇일까요?

// 입력
const xs: Array<number> = [1, 2, 3]

// 변환
const double = (n: number): number => n * 2

// 결과: `xs`의 각 요소가 2배가 되는 배열을 원합니다.
const ys: Array<number> = []
for (let i = 0; i <= xs.length; i++) {
  ys.push(double(xs[i]))
}

for 루프는 많은 유연성을 제공하며, 아래와 같이 수정할 수 있습니다.

• 시작 인덱스 let i = 0
• 반복 조건, i < xs.length
• 단계별 변경, i++.

이것은 또한 오류가 발생할 수 있으며 반환값을 보장할 수 없음을 의미합니다.

퀴즈: for 루프가 올바르게 작성되었나요?

정답은 여기에서 확인할 수 있습니다.

map을 사용하여 같은 예시를 다시 작성해 봅시다.

// 입력
const xs: Array<number> = [1, 2, 3]

// 변환
const double = (n: number): number => n * 2

// 결과: `xs`의 각 요소가 2배가 되는 배열을 원합니다.
const ys: Array<number> = xs.map(double)

map이 for 루프와 같은 유연성이 부족하다는 것을 알 수 있지만 몇 가지를 보장합니다.

• 입력 배열의 모든 요소가 처리됩니다.
• 결과 배열은 항상 시작 배열과 동일한 수의 요소를 갖습니다.

세부 구현보다 코드 속성에 중점을 두는 함수형 프로그래밍에서 map 연산은 제한으로 인해 흥미롭습니다.

for 루프보다 map이 포함된 Pull Request를 검토하는 것이 얼마나 쉬울지 생각해 보세요.

함수형 프로그래밍의 두 기둥

함수형 프로그래밍은 다음 두 기둥을 기반으로 합니다.

• 참조 투명성
• 합성 (일반적인 디자인 패턴으로)

나머지는 모두 이 두 지점에서 직접적, 간접적으로 파생됩니다.

참조 투명성

정의: 식은 프로그램의 동작을 변경하지 않고 해당 값으로 대체할 수 있는 경우 참조적으로 투명하다고 합니다.

예시 (참조 투명성은 순수 함수의 사용을 의미합니다.)

const double = (n: number): number => n * 2

const x = double(2)
const y = double(2)

double(2) 식은 숫자 4로 대체할 수 있기 때문에 참조 투명성을 가집니다.

따라서 다음과 같이 리팩토링을 진행할 수 있습니다.

const x = 4
const y = x

모든 표현식이 참조적으로 투명한 것은 아닙니다. 예시를 살펴보겠습니다.

예시 (참조 투명성은 예외를 던지지 않음을 의미합니다.)

const inverse = (n: number): number => {
  if (n === 0) throw new Error('cannot divide by zero')
  return 1 / n
}

const x = inverse(0) + 1

inverse(0)을 해당 값으로 대체할 수 없으므로 참조 투명성을 갖지 않습니다.

예시 (참조 투명성을 위해서는 불변 데이터 구조를 사용해야 합니다.)

const xs = [1, 2, 3]

const append = (xs: Array<number>): void => {
  xs.push(4)
}

append(xs)

const ys = xs

마지막 줄에서 xs는 append를 호출해 변경되었기 때문에 초기 값 [1, 2, 3]으로 대체할 수 없습니다.

참조 투명성이 왜 그렇게 중요할까요? 참조 투명성은 다음과 같은 이점이 있습니다.

• 지역적 코드에 대한 이유, 코드의 부분을 이해하기 위해 외부 맥락을 알 필요가 없습니다.
• 시스템 동작을 변경하지 않고 리팩터링을 할 수 있습니다.

퀴즈: 다음과 같은 프로그램이 있다고 가정해 봅시다.

// TypeScript에서 `declare`는 구현을 요구하지 않고 정의를 할 수 있습니다.
declare const question: (message: string) => Promise<string>

const x = await question('What is your name?')
const y = await question('What is your name?')

이런 방식으로 리팩토링을 할 수 있나요? 프로그램의 동작이 변경되나요? 아니면 변경될 예정인가요?

const x = await question('What is your name?')
const y = x

정답은 question의 구현을 읽지 않고는 알 수 있는 방법이 없습니다.

보시다시피 참조 투명하지 않은 표현식을 포함하는 프로그램을 리팩터링하는 것은 어려울 수 있습니다. 모든 표현식이 참조적으로 투명한 함수형 프로그래밍에서는 변경에 필요한 생각이 ​​크게 줄어듭니다.

합성

함수형 프로그래밍의 기본 패턴은 합성입니다. 매우 구체적인 작업을 수행하는 작은 코드 단위를 더 크고 복잡한 단위로 합성합니다.

우리가 생각할 수 있는 "가장 작은 것에서 가장 큰 것" 합성 패턴의 예시는 다음과 같습니다.

• 두 개 이상의 원시 값(숫자 또는 문자열) 합성
• 2개 이상의 함수 합성
• 전체 프로그램 합성

마지막 예에서 우리는 모듈성 프로그래밍에 대해 말할 수 있습니다.

모듈성 프로그래밍이란 작은 프로그램을 함께 붙여서 큰 프로그램을 만드는 과정을 의미합니다. - Simon Peyton Jones

이 프로그래밍 스타일은 결합자를 사용해 달성할 수 있습니다.

결합자라는 용어는 결합자 패턴을 참조합니다.

사물을 결합한다는 아이디어를 기반으로 라이브러리를 합성하는 방식입니다. 일반적으로 일부 T 타입, T 타입의 일부 "원시" 값 및 T 타입의 값을 다양한 방식으로 합성하여 T 타입보다 복잡한 값을 구축할 수 있는 일부 "결합자"가 있습니다.

결합자의 일반적인 개념은 다소 모호하고 다양한 형태로 나타날 수 있지만 가장 간단한 것은 다음과 같습니다.

combinator: Thing -> Thing

예시: double 함수는 두 개의 숫자를 결합합니다.

결합자의 목표는 이미 정의된 Thing에서 새로운 Thing를 생성하는 것입니다.

결합자의 출력인 새로운 Thing은 다른 프로그램과 결합자에 대한 입력으로 전달될 수 있기 때문에 이 패턴을 매우 강력하게 만드는 폭발적인 결합의 기회를 얻습니다.

예시

import { pipe } from 'fp-ts/function'

const double = (n: number): number => n * 2

console.log(pipe(2, double, double, double)) // => 16

따라서 함수형 모듈에서 볼 수 있는 일반적인 설계는 다음과 같습니다.

• 일부 T 타입에 대한 모델
• T 타입의 작은 "원시" 집합
• 더 큰 구조에서 원시 요소를 결합하기 위한 결합자 집합

이런 모듈을 구현해 봅시다.

데모

01_retry.ts

데모에서 볼 수 있듯이 3개의 원시 요소와 2개의 결합자로 꽤 복잡한 정책을 표현할 수 있었습니다.

하나의 새로운 원시 요소 또는 이미 정의된 것에 하나의 결합자를 추가하는 것만으로도 표현 가능성이 기하급수적으로 추가되는 방식을 생각해 보세요.

01_retry.ts에 있는 두 결합자 중에서 concat은 매우 강력한 함수형 프로그래밍 추상화인 세미그룹을 참조하기 때문에 특별히 언급됩니다.

세미그룹으로 합성 모델링하기

세미그룹은 두 개 이상의 값을 결합하는 방법입니다.

세미그룹은 대수이며 일반적으로 다음의 특정 조합으로 정의됩니다.

• 하나 이상의 집합
• 해당 집합에 대한 하나 이상의 연산
• 이전 연산에 대한 0개 이상의 법칙

대수은 수학자들이 아이디어를 가장 순수한 형태로 포착해 불필요한 모든 것을 제거하는 방법입니다.

대수이 수정될 때 유일하게 허용되는 연산은 자체 법칙에 따라 대수 자체에 의해 정의된 연산입니다.

대수는 인터페이스의 추상화로 생각할 수 있습니다.

인터페이스가 수정될 때 허용되는 유일한 연산은 자체 법률에 따라 인터페이스 자체에 의해 정의된 연산입니다.

세미그룹으로 들어가기 전에 먼저 대수의 예시인 마그마를 살펴보겠습니다.

마그마의 정의

Magma는 매우 간단한 대수입니다.

• 집합 또는 타입 (A)
• concat 연산
• 지켜야 할 법칙이 없습니다.

참고: 대부분의 경우 set과 type이라는 용어는 같은 의미로 사용할 수 있습니다.

TypeScript의 interface를 이용해 마그마를 모델링할 수 있습니다.

interface Magma<A> {
  readonly concat: (first: A, second: A) => A
}

따라서 우리는 대수의 요소를 가지고 있습니다.

• 집합 A
• 집합 A에 대한 concat 연산. 이 작업은 집합 A에서 닫혀있다고 합니다. 이는 결과에 연산을 적용하는 요소 A가 여전히 A의 요소임을 의미합니다. 결과는 여전히 A이므로 concat의 입력으로 다시 사용할 수 있으며 원하는 만큼 작업을 반복할 수 있습니다. 즉 concat은 A 타입에 대한 결합자입니다.

A가 number 타입인 Magma<A>의 구체적인 인스턴스를 구현해 봅시다.

import { Magma } from 'fp-ts/Magma'

const MagmaSub: Magma<number> = {
  concat: (first, second) => first - second
}

// helper
const getPipeableConcat = <A>(M: Magma<A>) => (second: A) => (first: A): A =>
  M.concat(first, second)

const concat = getPipeableConcat(MagmaSub)

// 사용 예시

import { pipe } from 'fp-ts/function'

pipe(10, concat(2), concat(3), concat(1), concat(2), console.log)
// => 2

퀴즈: concat이 닫혀있는 작업이라는 사실은 사소한 내용이 아닙니다. 만약 A가 JavaScript의 숫자 타입(양수 및 음수 부동 집합)이 아닌 자연수 집합(양의 정수)인 우리가 구현한 MagmaSub와 같이 concat을 사용해 Magma<Natural>을 정의할 수 있을까요? closure 속성이 유효하지 않은 자연수에 대한 다른 concat 작업을 생각할 수 있을까요?

정답은 여기에서 확인할 수 있습니다.

정의: A가 비어 있지 않은 집합이고 *가 닫혀있는(또는 내부적인) A인 이항 연산인 경우 (A, *) 쌍을 마그마라고 합니다.

마그마는 어떤 법칙도 따르지 않으며 폐쇠(closure) 요구 사항만 있습니다. 또 다른 법칙이 필요한 대수인 세미그룹을 보겠습니다.

세미그룹의 정의

concat 연산이 결합적인 Magma가 주어지면 세미그룹입니다.

"결합적"이라는 용어는 다음 방정식을 의미합니다.

(x * y) * z = x * (y * z)

// 또는
concat(concat(a, b), c) = concat(a, concat(b, c))

A인 모든 x, y, z에 적용됩니다.

결합법칙은 표현식에서 괄호에 대해 걱정할 필요가 없으며 간단히 x * y * z라고 쓸 수 있음을 알려줍니다. (모호함 없음)

예시

문자열 연결은 결합법칙의 이점을 제공합니다.

("a" + "b") + "c" = "a" + ("b" + "c") = "abc"

모든 세미그룹은 마그마이지만 모든 마그마가 세미그룹은 아닙니다.

예시

이전 MagmaSub는 concat 작업이 결합적이지 않기 때문에 세미그룹이 아닙니다.

import { pipe } from 'fp-ts/function'
import { Magma } from 'fp-ts/Magma'

const MagmaSub: Magma<number> = {
  concat: (first, second) => first - second
}

pipe(MagmaSub.concat(MagmaSub.concat(1, 2), 3), console.log) // => -4
pipe(MagmaSub.concat(1, MagmaSub.concat(2, 3)), console.log) // => 2

세미그룹은 병렬화 작업의 본질을 포착합니다.

결합법칙을 따르는 연산이 있다는 것을 안다면 계산을 두 개의 하위 계산으로 더 나눌 수 있고, 각각은 하위 계산으로 더 나눌 수 있습니다.

a * b * c * d * e * f * g * h = ((a * b) * (c * d)) * ((e * f) * (g * h))

곱셈은 병렬적으로 실행할 수 있습니다.

Magma와 Semigroup은 TypeScript의 인터페이스를 이용해 구현됩니다.

// fp-ts/lib/Semigroup.ts

interface Semigroup<A> extends Magma<A> {}

다음 법칙이 적용되어야 합니다.

• 결합법칙: S가 세미그룹인 경우 다음이 참이어야 합니다.

S.concat(S.concat(x, y), z) = S.concat(x, S.concat(y, z))

A 타입인 모든 x, y, z에 대해 만족해야 합니다.

참고: 안타깝게도 TypeScript의 타입 시스템을 이용해 이 법칙을 인코딩하는 것은 불가능합니다.

ReadonlyArray<string>에 대한 세미그룹을 구현해 보겠습니다.

import * as Se from 'fp-ts/Semigroup'

const Semigroup: Se.Semigroup<ReadonlyArray<string>> = {
  concat: (first, second) => first.concat(second)
}

concat이라는 이름은 배열에 대해 의미가 있지만(나중에 살펴보겠지만) 컨텍스트와 인스턴스를 구현하는 A 타입에 따라 concat 세미그룹 연산은 다른 해석과 의미를 가질 수 있습니다.

• "연결"
• "조합"
• "병합"
• "융합"
• "선택"
• "합"
• "치환"

그리고 다른 많은 것들이 있습니다.

예시

다음은 세미그룹 (number, +)를 구현하는 방법입니다. 여기서 +는 일반적인 숫자 덧셈입니다.

import { Semigroup } from 'fp-ts/Semigroup'

/** 덧셈을 하는 숫자 `Semigroup` */
const SemigroupSum: Semigroup<number> = {
  concat: (first, second) => first + second
}

퀴즈: 데모 01_retry.ts에 정의된 concat 결합자를 사용해 RetryPolicy 타입에 대한 Semigroup 인스턴스를 정의할 수 있을까요?

정답은 여기에서 확인할 수 있습니다.

다음은 세미그룹 (number, *)에 대한 구현입니다. 여기서 *는 일반적인 숫자 곱셈입니다.

import { Semigroup } from 'fp-ts/Semigroup'

/** 곱셈을 하는 숫자 `Semigroup` */
const SemigroupProduct: Semigroup<number> = {
  concat: (first, second) => first * second
}

참고: 숫자의 세미그룹에 대해 생각하는 것은 일반적인 실수이지만 동일한 타입 A에 대해 Semigroup<A>의 인스턴스를 더 많이 정의하는 것이 가능합니다. 우리는 number에 대해 덧셈 및 곱셈에서 세미그룹을 정의하는 방법을 살펴보았습니다. 동일한 작업을 공유하지만 타입이 다른 Semigroup을 가질 수도 있습니다. SemigroupSum은 number와 같은 부호 없는 부동 소수점 대신 자연수에서도 구현될 수 있었습니다.

string 타입을 사용하는 또 다른 예시가 있습니다.

import { Semigroup } from 'fp-ts/Semigroup'

const SemigroupString: Semigroup<string> = {
  concat: (first, second) => first + second
}

이번에는 boolean 타입을 사용하는 다른 두 가지 예시가 있습니다.

import { Semigroup } from 'fp-ts/Semigroup'

const SemigroupAll: Semigroup<boolean> = {
  concat: (first, second) => first && second
}

const SemigroupAny: Semigroup<boolean> = {
  concat: (first, second) => first || second
}

concatAll 함수

정의에 따라 concat은 매번 A의 두 요소만 결합합니다. 여러 개를 결합하는 것이 가능할까요?

concatAll 함수는 다음을 받습니다.

• 세미그룹의 인스턴스
• 초기값
• 요소 배열

import * as S from 'fp-ts/Semigroup'
import * as N from 'fp-ts/number'

const sum = S.concatAll(N.SemigroupSum)(2)

console.log(sum([1, 2, 3, 4])) // => 12

const product = S.concatAll(N.SemigroupProduct)(3)

console.log(product([1, 2, 3, 4])) // => 72

Quiz: 초기 값을 제공해야 하는 이유는 무엇인가요?

-> 정답은 여기에서 확인할 수 있습니다.

예시

JavaScript 표준 라이브러리에서 인기 있는 몇가지 기능을 다시 구현하여 concatAll을 응용하는 프로그램을 소개하겠습니다.

import * as B from 'fp-ts/boolean'
import { concatAll } from 'fp-ts/Semigroup'
import * as S from 'fp-ts/struct'

const every = <A>(predicate: (a: A) => boolean) => (
  as: ReadonlyArray<A>
): boolean => concatAll(B.SemigroupAll)(true)(as.map(predicate))

const some = <A>(predicate: (a: A) => boolean) => (
  as: ReadonlyArray<A>
): boolean => concatAll(B.SemigroupAny)(false)(as.map(predicate))

const assign: (as: ReadonlyArray<object>) => object = concatAll(
  S.getAssignSemigroup<object>()
)({})

퀴즈: 다음 세미그룹 예시는 법칙을 만족하나요?

정답은 여기에서 확인할 수 있습니다.

import { Semigroup } from 'fp-ts/Semigroup'

/** 항상 첫 번째 인자를 반환 */
const first = <A>(): Semigroup<A> => ({
  concat: (first, _second) => first
})

퀴즈: 다음 세미그룹 예시는 법칙을 만족하나요?

정답은 여기에서 확인할 수 있습니다.

import { Semigroup } from 'fp-ts/Semigroup'

/** 항상 두 번째 인자를 반환 */
const last = <A>(): Semigroup<A> => ({
  concat: (_first, second) => second
})

이중 세미그룹

세미그룹 인스턴스가 주어지면 피연산자가 결합되는 순서를 간단히 바꾸면 새로운 세미그룹 인스턴스를 얻을 수 있습니다.

import { pipe } from 'fp-ts/function'
import { Semigroup } from 'fp-ts/Semigroup'
import * as S from 'fp-ts/string'

// 이것은 세미그룹 결합자입니다.
const reverse = <A>(S: Semigroup<A>): Semigroup<A> => ({
  concat: (first, second) => S.concat(second, first)
})

pipe(S.Semigroup.concat('a', 'b'), console.log) // => 'ab'
pipe(reverse(S.Semigroup).concat('a', 'b'), console.log) // => 'ba'

퀴즈: 이 결합자는 일반적으로 concat 작업이 가환적이 아니기 때문에 의미가 있습니다. concat이 가환적인 예시와 그리고 그렇지 않은 예시를 찾을 수 있나요?

정답은 여기에서 확인할 수 있습니다.

세미그룹 활용하기

보다 복잡한 타입에 대해 세미그룹 인스턴스를 정의해 보겠습니다.

import * as N from 'fp-ts/number'
import { Semigroup } from 'fp-ts/Semigroup'

// 원점에서 시작하는 벡터 모델링
type Vector = {
  readonly x: number
  readonly y: number
}

// 두 벡터의 합 모델
const SemigroupVector: Semigroup<Vector> = {
  concat: (first, second) => ({
    x: N.SemigroupSum.concat(first.x, second.x),
    y: N.SemigroupSum.concat(first.y, second.y)
  })
}

예시

const v1: Vector = { x: 1, y: 1 }
const v2: Vector = { x: 1, y: 2 }

console.log(SemigroupVector.concat(v1, v2)) // => { x: 2, y: 3 }

보일러플레이트가 너무 많은가요? 좋은 소식은 세미그룹의 수학 이론에 따르면 각 필드에 대한 세미그룹 인스턴스를 구현할 수 있는 경우 Vector와 같은 구조체에 대한 세미그룹 인스턴스를 구현할 수 있다는 것입니다.

편리하게도 fp-ts/Semigroup 모듈은 struct 결합자를 사용할 수 있게합니다.

import { struct } from 'fp-ts/Semigroup'

// 두 벡터의 합 모델
const SemigroupVector: Semigroup<Vector> = struct({
  x: N.SemigroupSum,
  y: N.SemigroupSum
})

참고: 튜플로 동작하는 struct와 유사한 결합자 tuple이 있습니다.

import * as N from 'fp-ts/number'
import { Semigroup, tuple } from 'fp-ts/Semigroup'

// 원점에서 시작하는 벡터 모델링
type Vector = readonly [number, number]

// 두 벡터의 합 모델
const SemigroupVector: Semigroup<Vector> = tuple(N.SemigroupSum, N.SemigroupSum)

const v1: Vector = [1, 1]
const v2: Vector = [1, 2]

console.log(SemigroupVector.concat(v1, v2)) // => [2, 3]

퀴즈: Semigroup<A>이 주어지고 A의 middle을 선택한 경우 두 concat 매개변수 사이에 삽입하면 결과가 여전히 세미그룹이라는 것이 사실인가요?

import { pipe } from 'fp-ts/function'
import { Semigroup } from 'fp-ts/Semigroup'
import * as S from 'fp-ts/string'

export const intercalate = <A>(middle: A) => (
  S: Semigroup<A>
): Semigroup<A> => ({
  concat: (first, second) => S.concat(S.concat(first, middle), second)
})

const SemigroupIntercalate = pipe(S.Semigroup, intercalate('|'))

pipe(
  SemigroupIntercalate.concat('a', SemigroupIntercalate.concat('b', 'c')),
  console.log
) // => 'a|b|c'

모든 타입의 Semigroup 인스턴스 찾기

결합법칙은 매우 강력한 요구 사항입니다. 특정 타입 A가 주어졌을 때 A에 대한 결합성을 찾을 수 없다면 어떻게 될까요?

다음과 같이 정의된 User 타입이 있다고 가정해 봅시다.

type User = {
  readonly id: number
  readonly name: string
}

그리고 데이터베이스 안에는 동일한 User의 여러 복사본이 있습니다. (예시: 수정 사항에 대한 기록일 수 있습니다.)

// 내부 API
declare const getCurrent: (id: number) => User
declare const getHistory: (id: number) => ReadonlyArray<User>

공개 API를 구현해야 합니다.

export declare const getUser: (id: number) => User

일부 기준에 따라 모든 사본을 고려해야 합니다. 기준은 가장 최근 사본 또는 가장 오래된 사본 또는 현재 사본 등을 반환하는 것입니다.

당연히 각 기준에 대해 특정 API를 다음과 같이 정의할 수 있습니다.

export declare const getMostRecentUser: (id: number) => User
export declare const getLeastRecentUser: (id: number) => User
export declare const getCurrentUser: (id: number) => User
// 등등...

따라서 User 타입의 값을 반환하려면 모든 복사본을 고려하고 병합(또는 선택)해야 합니다. 즉, Semigroup<User>로 기준 문제를 모델링할 수 있습니다.

즉, "두 개의 사용자를 병합"하는 것이 무엇을 의미하는지, 이 병합 작업이 연관되는지 여부가 지금 당장은 명확하지 않습니다.

A 자체가 아닌 NonEmptyArray<A>에 대한 세미그룹 인스턴스를 정의하여 항상 주어진 타입 A에 대한 세미그룹 인스턴스인 자유 세미그룹을 정의할 수 있습니다.

import { Semigroup } from 'fp-ts/Semigroup'

// 비어 있지 않은 배열을 나타냅니다. 즉, 요소 ​​A가 하나 이상 있는 배열을 의미합니다.
type ReadonlyNonEmptyArray<A> = ReadonlyArray<A> & {
  readonly 0: A
}

// 두 NonEmptyArray의 연결은 여전히 ​​NonEmptyArray입니다.
const getSemigroup = <A>(): Semigroup<ReadonlyNonEmptyArray<A>> => ({
  concat: (first, second) => [first[0], ...first.slice(1), ...second]
})

그런 다음 A의 요소를 요소가 하나뿐인 배열을 의미하는 ReadonlyNonEmptyArray<A>의 "싱글톤"에 사상할 수 있습니다.

// 비어 있지 않은 배열에 요소 삽입
const of = <A>(a: A): ReadonlyNonEmptyArray<A> => [a]

이 기술을 User 타입에 적용해 보겠습니다.

import {
  getSemigroup,
  of,
  ReadonlyNonEmptyArray
} from 'fp-ts/ReadonlyNonEmptyArray'
import { Semigroup } from 'fp-ts/Semigroup'

type User = {
  readonly id: number
  readonly name: string
}

// 이 세미그룹은 `User` 타입이 아니라 `ReadonlyNonEmptyArray<User>`용입니다.
const S: Semigroup<ReadonlyNonEmptyArray<User>> = getSemigroup<User>()

declare const user1: User
declare const user2: User
declare const user3: User

// const merge: ReadonlyNonEmptyArray<User>
const merge = S.concat(S.concat(of(user1), of(user2)), of(user3))

// 사용자를 배열에 수동으로 "담아" 동일한 결과를 얻을 수 있습니다.
const merge2: ReadonlyNonEmptyArray<User> = [user1, user2, user3]

따라서 A의 자유 세미그룹은 요소가 모두 가능한 A의 유한 시퀀스인 비어 있지 않은 또 다른 세미그룹일 뿐입니다.

A의 자유 세미그룹은 데이터 내용을 보존하면서 A 타입의 요소를 concat하는 지연 방식으로 볼 수 있습니다.

[user1, user2, user3]을 포함하는 merge 값은 연결할 요소와 순서를 알려줍니다.

이제 getUser API를 설계할 수 있는 세 가지 가능한 옵션이 있습니다.

1. Semigroup<User>를 정의할 수 있으며 바로 병합하고 싶은 경우

declare const SemigroupUser: Semigroup<User>

export const getUser = (id: number): User => {
  const current = getCurrent(id)
  const history = getHistory(id)
  return concatAll(SemigroupUser)(current)(history)
}

2. Semigroup<User>를 정의할 수 없거나 병합 전략을 구현에 공개하고 싶기 때문에 API 소비자에게 요청하는 경우

export const getUser = (SemigroupUser: Semigroup<User>) => (
  id: number
): User => {
  const current = getCurrent(id)
  const history = getHistory(id)
  // 즉시 병합
  return concatAll(SemigroupUser)(current)(history)
}

3. Semigroup<User>를 정의할 수 없으며 요구하고 싶지 않은 경우

이 경우 User의 자유 세미그룹이 도움이 될 수 있습니다.

export const getUser = (id: number): ReadonlyNonEmptyArray<User> => {
  const current = getCurrent(id)
  const history = getHistory(id)
  // 병합을 진행하지 않고 User 자유 세미그룹을 반환합니다.
  return [current, ...history]
}

Semigroup<A> 인스턴스가 있는 경우에도 다음과 같은 이유로 자유 세미그룹을 사용하는 것이 편리할 수 있습니다.

• 비용이 많이 들고 무의미한 계산 실행을 방치하고 싶은 경우
• 세미그룹 인스턴스를 전달하고 싶지 않은 경우
• API 소비자가 올바른 병합 전략을 결정할 수 있는 경우 (concatAll 사용)

순서 추론이 가능한 세미그룹

주어진 number가 전순서인 경우(즉, x와 y를 선택하면 x <= y 또는 y <= x의 두 조건 중 하나가 참이어야 합니다.) min 또는 max 연산을 사용해 또 다른 두 개의 Semigroup<number> 인스턴스를 정의할 수 있습니다.

import { Semigroup } from 'fp-ts/Semigroup'

const SemigroupMin: Semigroup<number> = {
  concat: (first, second) => Math.min(first, second)
}

const SemigroupMax: Semigroup<number> = {
  concat: (first, second) => Math.max(first, second)
}

퀴즈: 숫자가 전순서라는 것이 왜 중요할까요?

number와 다른 타입에 대해 이런 세미그룹(SemigroupMin과 SemigroupMax)을 정의하는 것은 매우 유용합니다.

다른 타입에 대해 전순서 개념을 포착할 수 있나요?

순서에 대해 이야기하려면 먼저 동등성의 개념을 파악해야 합니다.

Modelling equivalence with Eq

Yet again, we can model the notion of equality.

Equivalence relations capture the concept of equality of elements of the same type. The concept of an equivalence relation can be implemented in TypeScript with the following interface:

interface Eq<A> {
  readonly equals: (first: A, second: A) => boolean
}

Intuitively:

• if equals(x, y) = true then we say x and y are equal
• if equals(x, y) = false then we say x and y are different

Example

This is an instance of Eq for the number type:

import { Eq } from 'fp-ts/Eq'
import { pipe } from 'fp-ts/function'

const EqNumber: Eq<number> = {
  equals: (first, second) => first === second
}

pipe(EqNumber.equals(1, 1), console.log) // => true
pipe(EqNumber.equals(1, 2), console.log) // => false

The following laws have to hold true:

1. Reflexivity: equals(x, x) === true, for every x in A
2. Symmetry: equals(x, y) === equals(y, x), for every x, y in A
3. Transitivity: if equals(x, y) === true and equals(y, z) === true, then equals(x, z) === true, for every x, y, z in A

Quiz. Would a combinator reverse: <A>(E: Eq<A>) => Eq<A> make sense?

Quiz. Would a combinator not: <A>(E: Eq<A>) => Eq<A> make sense?

import { Eq } from 'fp-ts/Eq'

export const not = <A>(E: Eq<A>): Eq<A> => ({
  equals: (first, second) => !E.equals(first, second)
})

Example

Let's see the first example of the usage of the Eq abstraction by defining a function elem that checks whether a given value is an element of ReadonlyArray.

import { Eq } from 'fp-ts/Eq'
import { pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'

// returns `true` if the element `a` is included in the list `as`
const elem = <A>(E: Eq<A>) => (a: A) => (as: ReadonlyArray<A>): boolean =>
  as.some((e) => E.equals(a, e))

pipe([1, 2, 3], elem(N.Eq)(2), console.log) // => true
pipe([1, 2, 3], elem(N.Eq)(4), console.log) // => false

Why would we not use the native includes Array method?

console.log([1, 2, 3].includes(2)) // => true
console.log([1, 2, 3].includes(4)) // => false

Let's define some Eq instance for more complex types.

import { Eq } from 'fp-ts/Eq'

type Point = {
  readonly x: number
  readonly y: number
}

const EqPoint: Eq<Point> = {
  equals: (first, second) => first.x === second.x && first.y === second.y
}

console.log(EqPoint.equals({ x: 1, y: 2 }, { x: 1, y: 2 })) // => true
console.log(EqPoint.equals({ x: 1, y: 2 }, { x: 1, y: -2 })) // => false

and check the results of elem and includes

const points: ReadonlyArray<Point> = [
  { x: 0, y: 0 },
  { x: 1, y: 1 },
  { x: 2, y: 2 }
]

const search: Point = { x: 1, y: 1 }

console.log(points.includes(search)) // => false :(
console.log(pipe(points, elem(EqPoint)(search))) // => true :)

Quiz (JavaScript). Why does the includes method returns false?

-> See the answer here

Abstracting the concept of equality is of paramount importance, especially in a language like JavaScript where some data types do not offer handy APIs for checking user-defined equality.

The JavaScript native Set datatype suffers by the same issue:

type Point = {
  readonly x: number
  readonly y: number
}

const points: Set<Point> = new Set([{ x: 0, y: 0 }])

points.add({ x: 0, y: 0 })

console.log(points)
// => Set { { x: 0, y: 0 }, { x: 0, y: 0 } }

Given the fact that Set uses === ("strict equality") for comparing values, points now contains two identical copies of { x: 0, y: 0 }, a result we definitely did not want. Thus it is convenient to define a new API to add an element to a Set, one that leverages the Eq abstraction.

Quiz. What would be the signature of this API?

Does EqPoint require too much boilerplate? The good news is that theory offers us yet again the possibility of implementing an Eq instance for a struct like Point if we are able to define an Eq instance for each of its fields.

Conveniently the fp-ts/Eq module exports a struct combinator:

import { Eq, struct } from 'fp-ts/Eq'
import * as N from 'fp-ts/number'

type Point = {
  readonly x: number
  readonly y: number
}

const EqPoint: Eq<Point> = struct({
  x: N.Eq,
  y: N.Eq
})

Note. Like for Semigroup, we aren't limited to struct-like data types, we also have combinators for working with tuples: tuple

import { Eq, tuple } from 'fp-ts/Eq'
import * as N from 'fp-ts/number'

type Point = readonly [number, number]

const EqPoint: Eq<Point> = tuple(N.Eq, N.Eq)

console.log(EqPoint.equals([1, 2], [1, 2])) // => true
console.log(EqPoint.equals([1, 2], [1, -2])) // => false

There are other combinators exported by fp-ts, here we can see a combinator that allows us to derive an Eq instance for ReadonlyArrays.

import { Eq, tuple } from 'fp-ts/Eq'
import * as N from 'fp-ts/number'
import * as RA from 'fp-ts/ReadonlyArray'

type Point = readonly [number, number]

const EqPoint: Eq<Point> = tuple(N.Eq, N.Eq)

const EqPoints: Eq<ReadonlyArray<Point>> = RA.getEq(EqPoint)

Similarly to Semigroups, it is possible to define more than one Eq instance for the same given type. Suppose we have modeled a User with the following type:

type User = {
  readonly id: number
  readonly name: string
}

we can define a "standard" Eq<User> instance using the struct combinator:

import { Eq, struct } from 'fp-ts/Eq'
import * as N from 'fp-ts/number'
import * as S from 'fp-ts/string'

type User = {
  readonly id: number
  readonly name: string
}

const EqStandard: Eq<User> = struct({
  id: N.Eq,
  name: S.Eq
})

Several languages, even pure functional languages like Haskell, do not allow to have more than one Eq instance per data type. But we may have different contexts where the meaning of User equality might differ. One common context is where two Users are equal if their id field is equal.

/** two users are equal if their `id` fields are equal */
const EqID: Eq<User> = {
  equals: (first, second) => N.Eq.equals(first.id, second.id)
}

Now that we made an abstract concept concrete by representing it as a data structure, we can programmatically manipulate Eq instances like we do with other data structures. Let's see an example.

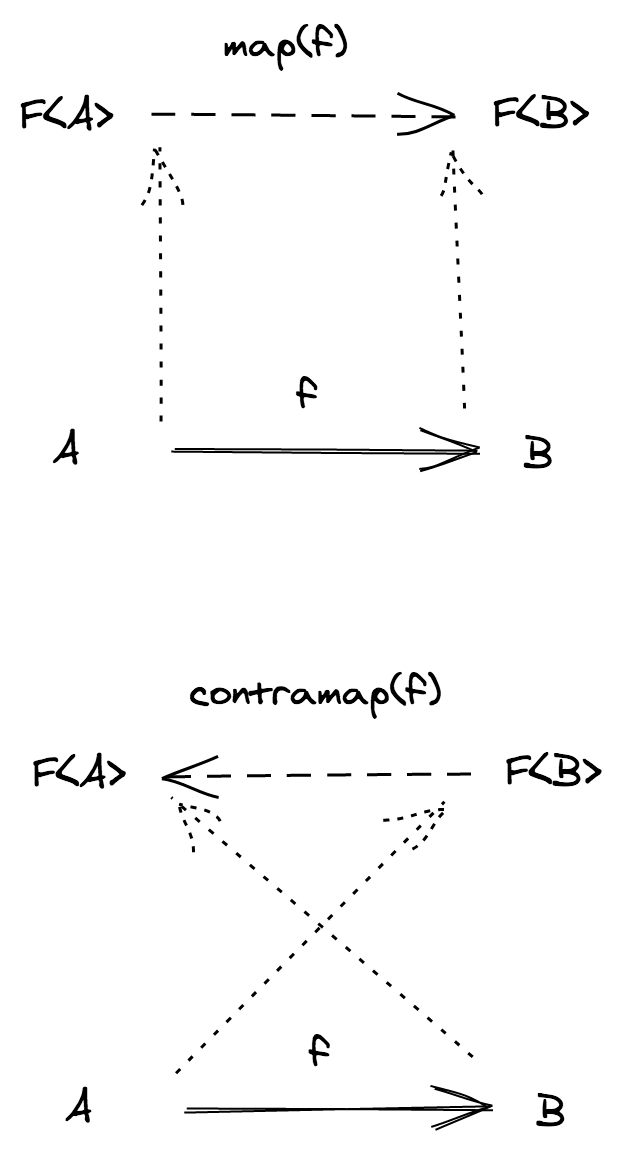
Example. Rather than manually defining EqId we can use the combinator contramap: given an instance Eq<A> and a function from B to A, we can derive an Eq<B>

import { Eq, struct, contramap } from 'fp-ts/Eq'
import { pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
import * as S from 'fp-ts/string'

type User = {
  readonly id: number
  readonly name: string
}

const EqStandard: Eq<User> = struct({
  id: N.Eq,
  name: S.Eq
})

const EqID: Eq<User> = pipe(
  N.Eq,
  contramap((user: User) => user.id)
)

console.log(
  EqStandard.equals({ id: 1, name: 'Giulio' }, { id: 1, name: 'Giulio Canti' })
) // => false (because the `name` property differs)

console.log(
  EqID.equals({ id: 1, name: 'Giulio' }, { id: 1, name: 'Giulio Canti' })
) // => true (even though the `name` property differs)

console.log(EqID.equals({ id: 1, name: 'Giulio' }, { id: 2, name: 'Giulio' }))
// => false (even though the `name` property is equal)

Quiz. Given a data type A, is it possible to define a Semigroup<Eq<A>>? What could it represent?

Modeling ordering relations with Ord

In the previous chapter regarding Eq we were dealing with the concept of equality. In this one we'll deal with the concept of ordering.

The concept of a total order relation can be implemented in TypeScript as following:

import { Eq } from 'fp-ts/lib/Eq'

type Ordering = -1 | 0 | 1

interface Ord<A> extends Eq<A> {
  readonly compare: (x: A, y: A) => Ordering
}

Resulting in:

• x < y if and only if compare(x, y) = -1
• x = y if and only if compare(x, y) = 0
• x > y if and only if compare(x, y) = 1

Example

Let's try to define an Ord instance for the type number:

import { Ord } from 'fp-ts/Ord'

const OrdNumber: Ord<number> = {
  equals: (first, second) => first === second,
  compare: (first, second) => (first < second ? -1 : first > second ? 1 : 0)
}

The following laws have to hold true:

1. Reflexivity: compare(x, x) <= 0, for every x in A
2. Antisymmetry: if compare(x, y) <= 0 and compare(y, x) <= 0 then x = y, for every x, y in A
3. Transitivity: if compare(x, y) <= 0 and compare(y, z) <= 0 then compare(x, z) <= 0, for every x, y, z in A

compare has also to be compatible with the equals operation from Eq:

compare(x, y) === 0 if and only if equals(x, y) === true, for every x, y in A

Note. equals can be derived from compare in the following way:

equals: (first, second) => compare(first, second) === 0

In fact the fp-ts/Ord module exports a handy helper fromCompare which allows us to define an Ord instance simply by supplying the compare function:

import { Ord, fromCompare } from 'fp-ts/Ord'

const OrdNumber: Ord<number> = fromCompare((first, second) =>
  first < second ? -1 : first > second ? 1 : 0
)

Quiz. Is it possible to define an Ord instance for the game Rock-Paper-Scissor where move1 <= move2 if move2 beats move1?

Let's see a practical usage of an Ord instance by defining a sort function which orders the elements of a ReadonlyArray.

import { pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
import { Ord } from 'fp-ts/Ord'

export const sort = <A>(O: Ord<A>) => (
  as: ReadonlyArray<A>
): ReadonlyArray<A> => as.slice().sort(O.compare)

pipe([3, 1, 2], sort(N.Ord), console.log) // => [1, 2, 3]

Quiz (JavaScript). Why does the implementation leverages the native Array slice method?

Let's see another Ord pratical usage by defining a min function that returns the smallest of two values:

import { pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
import { Ord } from 'fp-ts/Ord'

const min = <A>(O: Ord<A>) => (second: A) => (first: A): A =>
  O.compare(first, second) === 1 ? second : first

pipe(2, min(N.Ord)(1), console.log) // => 1

Dual Ordering

In the same way we could invert the concat operation to obtain the dual semigroup using the reverse combinator, we can invert the compare operation to get the dual ordering.

Let's define the reverse combinator for Ord:

import { pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
import { fromCompare, Ord } from 'fp-ts/Ord'

export const reverse = <A>(O: Ord<A>): Ord<A> =>
  fromCompare((first, second) => O.compare(second, first))

A usage example for reverse is obtaining a max function from the min one:

import { flow, pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
import { Ord, reverse } from 'fp-ts/Ord'

const min = <A>(O: Ord<A>) => (second: A) => (first: A): A =>
  O.compare(first, second) === 1 ? second : first

// const max: <A>(O: Ord<A>) => (second: A) => (first: A) => A
const max = flow(reverse, min)

pipe(2, max(N.Ord)(1), console.log) // => 2

The totality of ordering (meaning that given any x and y, one of the two conditions needs to hold true: x <= y or y <= z) may appear obvious when speaking about numbers, but that's not always the case. Let's see a slightly more complex scenario:

type User = {
  readonly name: string
  readonly age: number
}

It's not really clear when a User is "smaller or equal" than another User.

How can we define an Ord<User> instance?

That depends on the context, but a possible choice might be ordering Users by their age:

import * as N from 'fp-ts/number'
import { fromCompare, Ord } from 'fp-ts/Ord'

type User = {
  readonly name: string
  readonly age: number
}

const byAge: Ord<User> = fromCompare((first, second) =>
  N.Ord.compare(first.age, second.age)
)

Again we can get rid of some boilerplate using the contramap combinatorL given an Ord<A> instance and a function from B to A, it is possible to derive Ord<B>:

import { pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
import { contramap, Ord } from 'fp-ts/Ord'

type User = {
  readonly name: string
  readonly age: number
}

const byAge: Ord<User> = pipe(
  N.Ord,
  contramap((_: User) => _.age)
)

We can get the youngest of two Users using the previously defined min function.

// const getYounger: (second: User) => (first: User) => User
const getYounger = min(byAge)

pipe(
  { name: 'Guido', age: 50 },
  getYounger({ name: 'Giulio', age: 47 }),
  console.log
) // => { name: 'Giulio', age: 47 }

Quiz. In the fp-ts/ReadonlyMap module the following API is exposed:

/**
 * Get a sorted `ReadonlyArray` of the keys contained in a `ReadonlyMap`.
 */
declare const keys: <K>(
  O: Ord<K>
) => <A>(m: ReadonlyMap<K, A>) => ReadonlyArray<K>

why does this API requires an instance for Ord<K>?

Let's finally go back to the very first issue: defining two semigroups SemigroupMin and SemigroupMax for types different than number:

import { Semigroup } from 'fp-ts/Semigroup'

const SemigroupMin: Semigroup<number> = {
  concat: (first, second) => Math.min(first, second)
}

const SemigroupMax: Semigroup<number> = {
  concat: (first, second) => Math.max(first, second)
}

Now that we have the Ord abstraction we can do it:

import { pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
import { Ord, contramap } from 'fp-ts/Ord'
import { Semigroup } from 'fp-ts/Semigroup'

export const min = <A>(O: Ord<A>): Semigroup<A> => ({
  concat: (first, second) => (O.compare(first, second) === 1 ? second : first)
})

export const max = <A>(O: Ord<A>): Semigroup<A> => ({
  concat: (first, second) => (O.compare(first, second) === 1 ? first : second)
})

type User = {
  readonly name: string
  readonly age: number
}

const byAge: Ord<User> = pipe(
  N.Ord,
  contramap((_: User) => _.age)
)

console.log(
  min(byAge).concat({ name: 'Guido', age: 50 }, { name: 'Giulio', age: 47 })
) // => { name: 'Giulio', age: 47 }
console.log(
  max(byAge).concat({ name: 'Guido', age: 50 }, { name: 'Giulio', age: 47 })
) // => { name: 'Guido', age: 50 }

Example

Let's recap all of this with one final example (adapted from Fantas, Eel, and Specification 4: Semigroup).

Suppose we need to build a system where, in a database, there are records of customers implemented in the following way:

interface Customer {
  readonly name: string
  readonly favouriteThings: ReadonlyArray<string>
  readonly registeredAt: number // since epoch
  readonly lastUpdatedAt: number // since epoch
  readonly hasMadePurchase: boolean
}

For some reason, there might be duplicate records for the same person.

We need a merging strategy. Well, that's Semigroup's bread and butter!

import * as B from 'fp-ts/boolean'
import { pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
import { contramap } from 'fp-ts/Ord'
import * as RA from 'fp-ts/ReadonlyArray'
import { max, min, Semigroup, struct } from 'fp-ts/Semigroup'
import * as S from 'fp-ts/string'

interface Customer {
  readonly name: string
  readonly favouriteThings: ReadonlyArray<string>
  readonly registeredAt: number // since epoch
  readonly lastUpdatedAt: number // since epoch
  readonly hasMadePurchase: boolean
}

const SemigroupCustomer: Semigroup<Customer> = struct({
  // keep the longer name
  name: max(pipe(N.Ord, contramap(S.size))),
  // accumulate things
  favouriteThings: RA.getSemigroup<string>(),
  // keep the least recent date
  registeredAt: min(N.Ord),
  // keep the most recent date
  lastUpdatedAt: max(N.Ord),
  // boolean semigroup under disjunction
  hasMadePurchase: B.SemigroupAny
})

console.log(
  SemigroupCustomer.concat(
    {
      name: 'Giulio',
      favouriteThings: ['math', 'climbing'],
      registeredAt: new Date(2018, 1, 20).getTime(),
      lastUpdatedAt: new Date(2018, 2, 18).getTime(),
      hasMadePurchase: false
    },
    {
      name: 'Giulio Canti',
      favouriteThings: ['functional programming'],
      registeredAt: new Date(2018, 1, 22).getTime(),
      lastUpdatedAt: new Date(2018, 2, 9).getTime(),
      hasMadePurchase: true
    }
  )
)
/*
{ name: 'Giulio Canti',
  favouriteThings: [ 'math', 'climbing', 'functional programming' ],
  registeredAt: 1519081200000, // new Date(2018, 1, 20).getTime()
  lastUpdatedAt: 1521327600000, // new Date(2018, 2, 18).getTime()
  hasMadePurchase: true
}
*/

Quiz. Given a type A is it possible to define a Semigroup<Ord<A>> instance? What could it possibly represent?

데모

Modeling composition through Monoids

Let's recap what we have seen till now.

We have seen how an algebra is a combination of:

• some type A
• some operations involving the type A
• some laws and properties for that combination.

The first algebra we have seen has been the magma, an algebra defined on some type A equipped with one operation called concat. There were no laws involved in Magma<A> the only requirement we had was that the concat operation had to be closed on A meaning that the result:

concat(first: A, second: A) => A

has still to be an element of the A type.

Later on we have seen how adding one simple requirement, associativity, allowed some Magma<A> to be further refined as a Semigroup<A>, and how associativity captures the possibility of computations to be parallelized.

Now we're going to add another condition on Semigroup.

Given a Semigroup defined on some set A with some concat operation, if there is some element in A – we'll call this element empty – such as for every element a in A the two following equations hold true:

• Right identity: concat(a, empty) = a
• Left identity: concat(empty, a) = a

then the Semigroup is also a Monoid.

Note: We'll call the empty element unit for the rest of this section. There's other synonyms in literature, some of the most common ones are neutral element and identity_element.

We have seen how in TypeScript Magmas and Semigroups, can be modeled with interfaces, so it should not come as a surprise that the very same can be done for Monoids.

import { Semigroup } from 'fp-ts/Semigroup'

interface Monoid<A> extends Semigroup<A> {
  readonly empty: A
}

Many of the semigroups we have seen in the previous sections can be extended to become Monoids. All we need to find is some element of type A for which the Right and Left identities hold true.

import { Monoid } from 'fp-ts/Monoid'

/** number `Monoid` under addition */
const MonoidSum: Monoid<number> = {
  concat: (first, second) => first + second,
  empty: 0
}

/** number `Monoid` under multiplication */
const MonoidProduct: Monoid<number> = {
  concat: (first, second) => first * second,
  empty: 1
}

const MonoidString: Monoid<string> = {
  concat: (first, second) => first + second,
  empty: ''
}

/** boolean monoid under conjunction */
const MonoidAll: Monoid<boolean> = {
  concat: (first, second) => first && second,
  empty: true
}

/** boolean monoid under disjunction */
const MonoidAny: Monoid<boolean> = {
  concat: (first, second) => first || second,
  empty: false
}

Quiz. In the semigroup section we have seen how the type ReadonlyArray<string> admits a Semigroup instance:

import { Semigroup } from 'fp-ts/Semigroup'

const Semigroup: Semigroup<ReadonlyArray<string>> = {
  concat: (first, second) => first.concat(second)
}

Can you find the unit for this semigroup? If so, can we generalize the result not just for ReadonlyArray<string> but ReadonlyArray<A> as well?

Quiz (more complex). Prove that given a monoid, there can only be one unit.

The consequence of the previous proof is that there can be only one unit per monoid, once we find one we can stop searching.

We have seen how each semigroup was a magma, but not every magma was a semigroup. In the same way, each monoid is a semigroup, but not every semigroup is a monoid.

Example

Let's consider the following example:

import { pipe } from 'fp-ts/function'
import { intercalate } from 'fp-ts/Semigroup'
import * as S from 'fp-ts/string'

const SemigroupIntercalate = pipe(S.Semigroup, intercalate('|'))

console.log(S.Semigroup.concat('a', 'b')) // => 'ab'
console.log(SemigroupIntercalate.concat('a', 'b')) // => 'a|b'
console.log(SemigroupIntercalate.concat('a', '')) // => 'a|'

Note how for this Semigroup there's no such empty value of type string such as concat(a, empty) = a.

And now one final, slightly more "exotic" example, involving functions:

Example

An endomorphism is a function whose input and output type is the same:

type Endomorphism<A> = (a: A) => A

Given a type A, all endomorphisms defined on A are a monoid, such as:

• the concat operation is the usual function composition
• the unit, our empty value is the identity function

import { Endomorphism, flow, identity } from 'fp-ts/function'
import { Monoid } from 'fp-ts/Monoid'

export const getEndomorphismMonoid = <A>(): Monoid<Endomorphism<A>> => ({
  concat: flow,
  empty: identity
})

Note: The identity function has one, and only one possible implementation:

const identity = (a: A) => a

Whatever value we pass in input, it gives us the same value in output.

The concatAll function

One great property of monoids, compared to semigrops, is that the concatenation of multiple elements becomes even easier: it is not necessary anymore to provide an initial value.

import { concatAll } from 'fp-ts/Monoid'
import * as S from 'fp-ts/string'
import * as N from 'fp-ts/number'
import * as B from 'fp-ts/boolean'

console.log(concatAll(N.MonoidSum)([1, 2, 3, 4])) // => 10
console.log(concatAll(N.MonoidProduct)([1, 2, 3, 4])) // => 24
console.log(concatAll(S.Monoid)(['a', 'b', 'c'])) // => 'abc'
console.log(concatAll(B.MonoidAll)([true, false, true])) // => false
console.log(concatAll(B.MonoidAny)([true, false, true])) // => true

Quiz. Why is the initial value not needed anymore?

Product monoid

As we have already seen with semigroups, it is possible to define a monoid instance for a struct if we are able to define a monoid instance for each of its fields.

Example

import { Monoid, struct } from 'fp-ts/Monoid'
import * as N from 'fp-ts/number'

type Point = {
  readonly x: number
  readonly y: number
}

const Monoid: Monoid<Point> = struct({
  x: N.MonoidSum,
  y: N.MonoidSum
})

Note. There is a combinator similar to struct that works with tuples: tuple.

import { Monoid, tuple } from 'fp-ts/Monoid'
import * as N from 'fp-ts/number'

type Point = readonly [number, number]

const Monoid: Monoid<Point> = tuple(N.MonoidSum, N.MonoidSum)

Quiz. Is it possible to define a "free monoid" for a generic type A?

데모 (implementing a system to draw geoetric shapes on canvas)

03_shapes.ts

Pure and partial functions

In the first chapter we've seen an informal definition of a pure function:

A pure function is a procedure that given the same input always returns the same output and does not have any observable side effect.

Such an informal statement could leave space for some doubts, such as:

• what is a "side effect"?
• what does it means "observable"?
• what does it mean "same"?

Let's see a formal definition of the concept of a function.

Note. If X and Y are sets, then with X × Y we indicate their cartesian product, meaning the set

X × Y = { (x, y) | x ∈ X, y ∈ Y }

The following definition was given a century ago:

Definition. A _function: f: X ⟶ Y is a subset of X × Y such as for every x ∈ X there's exactly one y ∈ Y such that (x, y) ∈ f.

The set X is called the domain of f, Y is it's codomain.

Example

The function double: Nat ⟶ Nat is the subset of the cartesian product Nat × Nat given by { (1, 2), (2, 4), (3, 6), ...}.

In TypeScript we could define f as

const f: Record<number, number> = {
  1: 2,
  2: 4,
  3: 6
  ...
}

The one in the example is called an extensional definition of a function, meaning we enumerate one by one each of the elements of its domain and for each one of them we point the corresponding codomain element.

Naturally, when such a set is infinite this proves to be problematic. We can't list the entire domain and codomain of all functions.

We can get around this issue by introducing the one that is called intensional definition, meaning that we express a condition that has to hold for every couple (x, y) ∈ f meaning y = x * 2.

This the familiar form in which we write the double function and its definition in TypeScript:

const double = (x: number): number => x * 2

The definition of a function as a subset of a cartesian product shows how in mathematics every function is pure: there is no action, no state mutation or elements being modified. In functional programming the implementation of functions has to follow as much as possible this ideal model.

Quiz. Which of the following procedures are pure functions?

const coefficient1 = 2
export const f1 = (n: number) => n * coefficient1

// ------------------------------------------------------

let coefficient2 = 2
export const f2 = (n: number) => n * coefficient2++

// ------------------------------------------------------

let coefficient3 = 2
export const f3 = (n: number) => n * coefficient3

// ------------------------------------------------------

export const f4 = (n: number) => {
  const out = n * 2
  console.log(out)
  return out
}

// ------------------------------------------------------

interface User {
  readonly id: number
  readonly name: string
}

export declare const f5: (id: number) => Promise<User>

// ------------------------------------------------------

import * as fs from 'fs'

export const f6 = (path: string): string =>
  fs.readFileSync(path, { encoding: 'utf8' })

// ------------------------------------------------------

export const f7 = (
  path: string,
  callback: (err: Error | null, data: string) => void
): void => fs.readFile(path, { encoding: 'utf8' }, callback)

The fact that a function is pure does not imply automatically a ban on local mutability as long as it doesn't leaks out of its scope.

Example (Implementazion details of the concatAll function for monoids)

import { Monoid } from 'fp-ts/Monoid'

const concatAll = <A>(M: Monoid<A>) => (as: ReadonlyArray<A>): A => {
  let out: A = M.empty // <= local mutability
  for (const a of as) {
    out = M.concat(out, a)
  }
  return out
}

The ultimate goal is to guarantee: referential transparency.

The contract we sign with a user of our APIs is defined by the APIs signature:

declare const concatAll: <A>(M: Monoid<A>) => (as: ReadonlyArray<A>) => A

and by the promise of respecting referential transparency. The technical details of how the function is implemented are not relevant, thus there is maximum freedom implementation-wise.

Thus, how do we define a "side effect"? Simply by negating referential transparency:

An expression contains "side effects" if it doesn't benefit from referential transparency

Not only functions are a perfect example of one of the two pillars of functional programming, referential transparency, but they're also examples of the second pillar: composition.

Functions compose:

Definition. Given f: Y ⟶ Z and g: X ⟶ Y two functions, then the function h: X ⟶ Z defined by:

h(x) = f(g(x))

is called composition of f and g and is written h = f ∘ g

Please note that in order for f and g to combine, the domain of f has to be included in the codomain of g.

Definition. A function is said to be partial if it is not defined for each value of its domain.

Vice versa, a function defined for all values of its domain is said to be total

Example

f(x) = 1 / x

The function f: number ⟶ number is not defined for x = 0.

Example

// Get the first element of a `ReadonlyArray`
declare const head: <A>(as: ReadonlyArray<A>) => A

Quiz. Why is the head function partial?

Quiz. Is JSON.parse a total function?

parse: (text: string, reviver?: (this: any, key: string, value: any) => any) =>
  any

Quiz. Is JSON.stringify a total function?

stringify: (
  value: any,
  replacer?: (this: any, key: string, value: any) => any,
  space?: string | number
) => string

In functional programming there is a tendency to only define pure and total functions. From now on with the term function we'll be specifically referring to "pure and total function". So what do we do when we have a partial function in our applications?

A partial function f: X ⟶ Y can always be "brought back" to a total one by adding a special value, let's call it None, to the codomain and by assigning it to the output of f for every value of X where the function is not defined.

f': X ⟶ Y ∪ None

Let's call it Option(Y) = Y ∪ None.

f': X ⟶ Option(Y)

In functional programming the tendency is to define only pure and and total functions.

Is it possible to define Option in TypeScript? In the following chapters we'll see how to do it.

Algebraic Data Types

A good first step when writing an application or feature is to define it's domain model. TypeScript offers many tools that help accomplishing this task. Algebraic Data Types (in short, ADTs) are one of these tools.

What is an ADT?

In computer programming, especially functional programming and type theory, an algebraic data type is a kind of composite type, i.e., a type formed by combining other types.

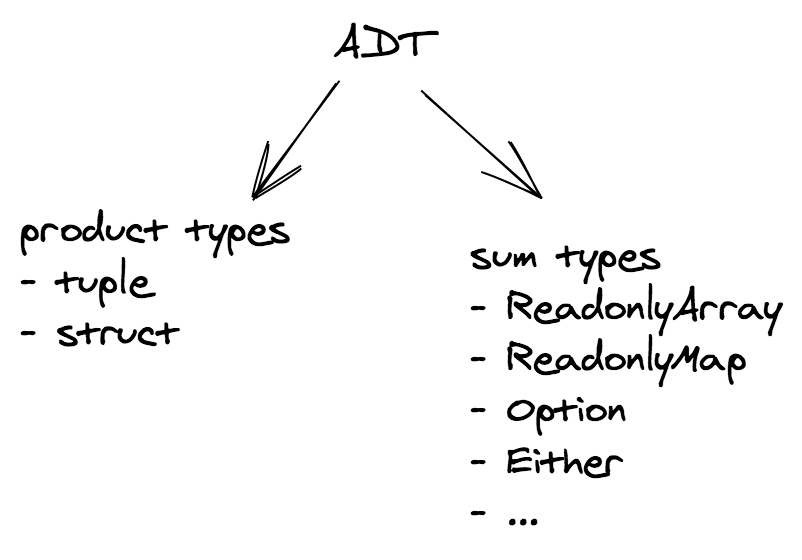
Two common families of algebraic data types are:

• product types
• sum types

Let's begin with the more familiar ones: product types.

Product types

A product type is a collection of types T_i indexed by a set I.

Two members of this family are n-tuples, where I is an interval of natural numbers:

type Tuple1 = [string] // I = [0]
type Tuple2 = [string, number] // I = [0, 1]
type Tuple3 = [string, number, boolean] // I = [0, 1, 2]

// Accessing by index
type Fst = Tuple2[0] // string
type Snd = Tuple2[1] // number

and structs, where I is a set of labels:

// I = {"name", "age"}
interface Person {
  name: string
  age: number
}

// Accessing by label
type Name = Person['name'] // string
type Age = Person['age'] // number

Product types can be polimorphic.

Example

//                ↓ type parameter
type HttpResponse<A> = {
  readonly code: number
  readonly body: A
}

Why "product" types?

If we label with C(A) the number of elements of type A (also called in mathematics, cardinality), then the following equation hold true:

C([A, B]) = C(A) * C(B)

the cardinality of a product is the product of the cardinalities

Example

The null type has cardinality 1 because it has only one member: null.

Quiz: What is the cardinality of the boolean type.

Example

type Hour = 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12
type Period = 'AM' | 'PM'
type Clock = [Hour, Period]

Type Hour has 12 members. Type Period has 2 members. Thus type Clock has 12 * 2 = 24 elements.

Quiz: What is the cardinality of the following Clock type?

// same as before
type Hour = 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12
// same as before
type Period = 'AM' | 'PM'

// different encoding, no longer a Tuple
type Clock = {
  readonly hour: Hour
  readonly period: Period
}

When can I use a product type?

Each time it's components are independent.

type Clock = [Hour, Period]

Here Hour and Period are independent: the value of Hour does not change the value of Period. Every legal pair of [Hour, Period] makes "sense" and is legal.

Sum types

A sum type is a a data type that can hold a value of different (but limited) types. Only one of these types can be used in a single instance and there is generally a "tag" value differentiating those types.

In TypeScript's official docs they are called discriminated union.

It is important to note that the members of the union have to be disjoint, there can't be values that belong to more than one member.

Example

The type:

type StringsOrNumbers = ReadonlyArray<string> | ReadonlyArray<number>

declare const sn: StringsOrNumbers

sn.map() // error: This expression is not callable.

is not a disjoint union because the value [], the empty array, belongs to both members.

Quiz. Is the following union disjoint?

type Member1 = { readonly a: string }
type Member2 = { readonly b: number }
type MyUnion = Member1 | Member2

Disjoint unions are recurring in functional programming.

Fortunately TypeScript has a way to guarantee that a union is disjoint: add a specific field that works as a tag.

Note: Disjoint unions, sum types and tagged unions are used interchangeably to indicate the same thing.

Example (redux actions)

The Action sum type models a portion of the operation that the user can take i a todo app.

type Action =
  | {
      type: 'ADD_TODO'
      text: string
    }
  | {
      type: 'UPDATE_TODO'
      id: number
      text: string
      completed: boolean
    }
  | {
      type: 'DELETE_TODO'
      id: number
    }

The type tag makes sure every member of the union is disjointed.

Note. The name of the field that acts as a tag is chosen by the developer. It doesn't have to be "type". In fp-ts the convention is to use a _tag field.

Now that we've seen few examples we can define more explicitly what algebraic data types are:

In general, an algebraic data type specifies a sum of one or more alternatives, where each alternative is a product of zero or more fields.

Sum types can be polymorphic and recursive.

Example (linked list)

//               ↓ type parameter
export type List<A> =
  | { readonly _tag: 'Nil' }
  | { readonly _tag: 'Cons'; readonly head: A; readonly tail: List<A> }
//                                                              ↑ recursion

Quiz (TypeScript). Which of the following data types is a product or a sum type?

• ReadonlyArray<A>
• Record<string, A>
• Record<'k1' | 'k2', A>
• ReadonlyMap<string, A>
• ReadonlyMap<'k1' | 'k2', A>

Constructors

A sum type with n elements needs at least n constructors, one for each member:

Example (redux action creators)

export type Action =
  | {
      readonly type: 'ADD_TODO'
      readonly text: string
    }
  | {
      readonly type: 'UPDATE_TODO'
      readonly id: number
      readonly text: string
      readonly completed: boolean
    }
  | {
      readonly type: 'DELETE_TODO'
      readonly id: number
    }

export const add = (text: string): Action => ({
  type: 'ADD_TODO',
  text
})

export const update = (
  id: number,
  text: string,
  completed: boolean
): Action => ({
  type: 'UPDATE_TODO',
  id,
  text,
  completed
})

export const del = (id: number): Action => ({
  type: 'DELETE_TODO',
  id
})

Example (TypeScript, linked lists)

export type List<A> =
  | { readonly _tag: 'Nil' }
  | { readonly _tag: 'Cons'; readonly head: A; readonly tail: List<A> }

// a nullary constructor can be implemented as a constant
export const nil: List<never> = { _tag: 'Nil' }

export const cons = <A>(head: A, tail: List<A>): List<A> => ({
  _tag: 'Cons',
  head,
  tail
})

// equivalent to an array containing [1, 2, 3]
const myList = cons(1, cons(2, cons(3, nil)))

Pattern matching

JavaScript doesn't support pattern matching (neither does TypeScript) but we can simulate it with a match function.

Example (TypeScript, linked lists)

interface Nil {
  readonly _tag: 'Nil'
}

interface Cons<A> {
  readonly _tag: 'Cons'
  readonly head: A
  readonly tail: List<A>
}

export type List<A> = Nil | Cons<A>

export const match = <R, A>(
  onNil: () => R,
  onCons: (head: A, tail: List<A>) => R
) => (fa: List<A>): R => {
  switch (fa._tag) {
    case 'Nil':
      return onNil()
    case 'Cons':
      return onCons(fa.head, fa.tail)
  }
}

// returns `true` if the list is empty
export const isEmpty = match(
  () => true,
  () => false
)

// returns the first element of the list or `undefined`
export const head = match(
  () => undefined,
  (head, _tail) => head
)

// returns the length of the list, recursively
export const length: <A>(fa: List<A>) => number = match(
  () => 0,
  (_, tail) => 1 + length(tail)
)

Quiz. Why's the head API sub optimal?

-> See the answer here

Note. TypeScript offers a great feature for sum types: exhaustive check. The type checker can check, no pun intended, whether all the possible cases are handled by the switch defined in the body of the function.

Why "sum" types?

Because the following identity holds true:

C(A | B) = C(A) + C(B)

The sum of the cardinality is the sum of the cardinalities

Example (the Option type)

interface None {
  readonly _tag: 'None'
}

interface Some<A> {
  readonly _tag: 'Some'
  readonly value: A
}

type Option<A> = None | Some<A>

From the general formula C(Option<A>) = 1 + C(A) we can derive the cardinality of the Option<boolean> type: 1 + 2 = 3 members.

When should I use a sum type?

When the components would be dependent if implemented with a product type.

Example (React props)

import * as React from 'react'

interface Props {
  readonly editable: boolean
  readonly onChange?: (text: string) => void
}

class Textbox extends React.Component<Props> {
  render() {
    if (this.props.editable) {
      // error: Cannot invoke an object which is possibly 'undefined' :(
      this.props.onChange('a')
    }
    return <div />
  }
}

The problem here is that Props is modeled like a product, but onChange depends on editable.

A sum type fits the use case better:

import * as React from 'react'

type Props =
  | {
      readonly type: 'READONLY'
    }
  | {
      readonly type: 'EDITABLE'
      readonly onChange: (text: string) => void
    }

class Textbox extends React.Component<Props> {
  render() {
    switch (this.props.type) {
      case 'EDITABLE':
        this.props.onChange('a') // :)
    }
    return <div />
  }
}

Example (node callbacks)

declare function readFile(
  path: string,
  //         ↓ ---------- ↓ CallbackArgs
  callback: (err?: Error, data?: string) => void
): void

The result of the readFile operation is modeled like a product type (to be more precise, as a tuple) which is later on passed to the callback function:

type CallbackArgs = [Error | undefined, string | undefined]

the callback components though are dependent: we either get an Error or a string:

err	data	legal?
Error	undefined	✓
undefined	string	✓
Error	string	✘
undefined	undefined	✘

This API is clearly not modeled on the following premise:

Make impossible state unrepresentable

A sum type would've been a better choice, but which sum type? We'll see how to handle errors in a functional way.

Quiz. Recently API's based on callbacks have been largely replaced by their Promise equivalents.

declare function readFile(path: string): Promise<string>

Can you find some cons of the Promise solution when using static typing like in TypeScript?

Functional error handling

Let's see how to handle errors in a functional way.

A function that returns errors or throws exceptions is an example of a partial function.

In the previous chapters we have seen that every partial function f can always be brought back to a total one f'.

f': X ⟶ Option(Y)

Now that we know a bit more about sum types in TypeScript we can define the Option without much issues.

The Option type

The type Option represents the effect of a computation which may fail (case None) or return a type A (case Some<A>):

// represents a failure
interface None {
  readonly _tag: 'None'
}

// represents a success
interface Some<A> {
  readonly _tag: 'Some'
  readonly value: A
}

type Option<A> = None | Some<A>

Constructors and pattern matching:

const none: Option<never> = { _tag: 'None' }

const some = <A>(value: A): Option<A> => ({ _tag: 'Some', value })

const match = <R, A>(onNone: () => R, onSome: (a: A) => R) => (
  fa: Option<A>
): R => {
  switch (fa._tag) {
    case 'None':
      return onNone()
    case 'Some':
      return onSome(fa.value)
  }
}

The Option type can be used to avoid throwing exceptions or representing the optional values, thus we can move from:

//                        this is a lie ↓
const head = <A>(as: ReadonlyArray<A>): A => {
  if (as.length === 0) {
    throw new Error('Empty array')
  }
  return as[0]
}

let s: string
try {
  s = String(head([]))
} catch (e) {
  s = e.message
}

where the type system is ignorant about the possibility of failure, to:

import { pipe } from 'fp-ts/function'

//                                      ↓ the type system "knows" that this computation may fail
const head = <A>(as: ReadonlyArray<A>): Option<A> =>
  as.length === 0 ? none : some(as[0])

declare const numbers: ReadonlyArray<number>

const result = pipe(
  head(numbers),
  match(
    () => 'Empty array',
    (n) => String(n)
  )
)

where the possibility of an error is encoded in the type system.

If we attempt to access the value property of an Option without checking in which case we are, the type system will warn us about the possibility of getting an error:

declare const numbers: ReadonlyArray<number>

const result = head(numbers)
result.value // type checker error: Property 'value' does not exist on type 'Option<number>'

The only way to access the value contained in an Option is to handle also the failure case using the match function.

pipe(result, match(
  () => ...handle error...
  (n) => ...go on with my business logic...
))

Is it possible to define instances for the abstractions we've seen in the chapters before? Let's begin with Eq.

An Eq instance

Suppose we have two values of type Option<string> and that we want to compare them to check if their equal:

import { pipe } from 'fp-ts/function'
import { match, Option } from 'fp-ts/Option'

declare const o1: Option<string>
declare const o2: Option<string>

const result: boolean = pipe(
  o1,
  match(
    // onNone o1
    () =>
      pipe(
        o2,
        match(
          // onNone o2
          () => true,
          // onSome o2
          () => false
        )
      ),
    // onSome o1
    (s1) =>
      pipe(
        o2,
        match(
          // onNone o2
          () => false,
          // onSome o2
          (s2) => s1 === s2 // <= qui uso l'uguaglianza tra stringhe
        )
      )
  )
)

What if we had two values of type Option<number>? It would be pretty annoying to write the same code we just wrote above, the only difference afterall would be how we compare the two values contained in the Option.

Thus we can generalize the necessary code by requiring the user to provide an Eq instance for A and then derive an Eq instance for Option<A>.

In other words we can define a combinator getEq: given an Eq<A> this combinator will return an Eq<Option<A>>:

import { Eq } from 'fp-ts/Eq'
import { pipe } from 'fp-ts/function'
import { match, Option, none, some } from 'fp-ts/Option'

export const getEq = <A>(E: Eq<A>): Eq<Option<A>> => ({
  equals: (first, second) =>
    pipe(
      first,
      match(
        () =>
          pipe(
            second,
            match(
              () => true,
              () => false
            )
          ),
        (a1) =>
          pipe(
            second,
            match(
              () => false,
              (a2) => E.equals(a1, a2) // <= here I use the `A` equality
            )
          )
      )
    )
})

import * as S from 'fp-ts/string'

const EqOptionString = getEq(S.Eq)

console.log(EqOptionString.equals(none, none)) // => true
console.log(EqOptionString.equals(none, some('b'))) // => false
console.log(EqOptionString.equals(some('a'), none)) // => false
console.log(EqOptionString.equals(some('a'), some('b'))) // => false
console.log(EqOptionString.equals(some('a'), some('a'))) // => true

The best thing about being able to define an Eq instance for a type Option<A> is being able to leverage all of the combiners we've seen previously for Eq.

Example:

An Eq instance for the type Option<readonly [string, number]>:

import { tuple } from 'fp-ts/Eq'
import * as N from 'fp-ts/number'
import { getEq, Option, some } from 'fp-ts/Option'
import * as S from 'fp-ts/string'

type MyTuple = readonly [string, number]

const EqMyTuple = tuple<MyTuple>(S.Eq, N.Eq)

const EqOptionMyTuple = getEq(EqMyTuple)

const o1: Option<MyTuple> = some(['a', 1])
const o2: Option<MyTuple> = some(['a', 2])
const o3: Option<MyTuple> = some(['b', 1])

console.log(EqOptionMyTuple.equals(o1, o1)) // => true
console.log(EqOptionMyTuple.equals(o1, o2)) // => false
console.log(EqOptionMyTuple.equals(o1, o3)) // => false

If we slightly modify the imports in the following snippet we can obtain a similar result for Ord:

import * as N from 'fp-ts/number'
import { getOrd, Option, some } from 'fp-ts/Option'
import { tuple } from 'fp-ts/Ord'
import * as S from 'fp-ts/string'

type MyTuple = readonly [string, number]

const OrdMyTuple = tuple<MyTuple>(S.Ord, N.Ord)

const OrdOptionMyTuple = getOrd(OrdMyTuple)

const o1: Option<MyTuple> = some(['a', 1])
const o2: Option<MyTuple> = some(['a', 2])
const o3: Option<MyTuple> = some(['b', 1])

console.log(OrdOptionMyTuple.compare(o1, o1)) // => 0
console.log(OrdOptionMyTuple.compare(o1, o2)) // => -1
console.log(OrdOptionMyTuple.compare(o1, o3)) // => -1

Semigroup and Monoid instances

Now, let's suppose we want to "merge" two different Option<A>s,: there are four different cases:

x	y	concat(x, y)
none	none	none
some(a)	none	none
none	some(a)	none
some(a)	some(b)	?

There's an issue in the last case, we need a recipe to "merge" two different As.

If only we had such a recipe..Isn't that the job our old good friends Semigroups!?

x	y	concat(x, y)
some(a1)	some(a2)	some(S.concat(a1, a2))

All we need to do is to require the user to provide a Semigroup instance for A and then derive a Semigroup instance for Option<A>.

// the implementation is left as an exercise for the reader
declare const getApplySemigroup: <A>(S: Semigroup<A>) => Semigroup<Option<A>>

Quiz. Is it possible to add a neutral element to the previous semigroup to make it a monoid?

// the implementation is left as an exercise for the reader
declare const getApplicativeMonoid: <A>(M: Monoid<A>) => Monoid<Option<A>>

It is possible to define a monoid instance for Option<A> that behaves like that:

x	y	concat(x, y)
none	none	none
some(a1)	none	some(a1)
none	some(a2)	some(a2)
some(a1)	some(a2)	some(S.concat(a1, a2))

// the implementation is left as an exercise for the reader
declare const getMonoid: <A>(S: Semigroup<A>) => Monoid<Option<A>>

Quiz. What is the empty member for the monoid?

-> See the answer here

Example

Using getMonoid we can derive another two useful monoids:

(Monoid returning the left-most non-None value)

x	y	concat(x, y)
none	none	none
some(a1)	none	some(a1)
none	some(a2)	some(a2)
some(a1)	some(a2)	some(a1)

import { Monoid } from 'fp-ts/Monoid'
import { getMonoid, Option } from 'fp-ts/Option'
import { first } from 'fp-ts/Semigroup'

export const getFirstMonoid = <A = never>(): Monoid<Option<A>> =>
  getMonoid(first())

and its dual:

(Monoid returning the right-most non-None value)

x	y	concat(x, y)
none	none	none
some(a1)	none	some(a1)
none	some(a2)	some(a2)
some(a1)	some(a2)	some(a2)

import { Monoid } from 'fp-ts/Monoid'
import { getMonoid, Option } from 'fp-ts/Option'
import { last } from 'fp-ts/Semigroup'

export const getLastMonoid = <A = never>(): Monoid<Option<A>> =>
  getMonoid(last())

Example

getLastMonoid can be useful to manage optional values. Let's seen an example where we want to derive user settings for a text editor, in this case VSCode.

import { Monoid, struct } from 'fp-ts/Monoid'
import { getMonoid, none, Option, some } from 'fp-ts/Option'
import { last } from 'fp-ts/Semigroup'

/** VSCode settings */
interface Settings {
  /** Controls the font family */
  readonly fontFamily: Option<string>
  /** Controls the font size in pixels */
  readonly fontSize: Option<number>
  /** Limit the width of the minimap to render at most a certain number of columns. */
  readonly maxColumn: Option<number>
}

const monoidSettings: Monoid<Settings> = struct({
  fontFamily: getMonoid(last()),
  fontSize: getMonoid(last()),
  maxColumn: getMonoid(last())
})

const workspaceSettings: Settings = {
  fontFamily: some('Courier'),
  fontSize: none,
  maxColumn: some(80)
}

const userSettings: Settings = {
  fontFamily: some('Fira Code'),
  fontSize: some(12),
  maxColumn: none
}

/** userSettings overrides workspaceSettings */
console.log(monoidSettings.concat(workspaceSettings, userSettings))
/*
{ fontFamily: some("Fira Code"),
  fontSize: some(12),
  maxColumn: some(80) }
*/

Quiz. Suppose VSCode cannot manage more than 80 columns per row, how could we modify the definition of monoidSettings to take that into account?

The Either type

We have seen how the Option data type can be used to handle partial functions, which often represent computations than can fail or throw exceptions.

This data type might be limiting in some use cases tho. While in the case of success we get Some<A> which contains information of type A, the other member, None does not carry any data. We know it failed, but we don't know the reason.

In order to fix this we simply need to another data type to represent failure, we'll call it Left<E>. We'll also replace the Some<A> type with the Right<A>.

// represents a failure
interface Left<E> {
  readonly _tag: 'Left'
  readonly left: E
}

// represents a success
interface Right<A> {
  readonly _tag: 'Right'
  readonly right: A
}

type Either<E, A> = Left<E> | Right<A>

Constructors and pattern matching:

const left = <E, A>(left: E): Either<E, A> => ({ _tag: 'Left', left })

const right = <A, E>(right: A): Either<E, A> => ({ _tag: 'Right', right })

const match = <E, R, A>(onLeft: (left: E) => R, onRight: (right: A) => R) => (
  fa: Either<E, A>
): R => {
  switch (fa._tag) {
    case 'Left':
      return onLeft(fa.left)
    case 'Right':
      return onRight(fa.right)
  }
}

Let's get back to the previous callback example:

declare function readFile(
  path: string,
  callback: (err?: Error, data?: string) => void
): void

readFile('./myfile', (err, data) => {
  let message: string
  if (err !== undefined) {
    message = `Error: ${err.message}`
  } else if (data !== undefined) {
    message = `Data: ${data.trim()}`
  } else {
    // should never happen
    message = 'The impossible happened'
  }
  console.log(message)
})

we can change it's signature to:

declare function readFile(
  path: string,
  callback: (result: Either<Error, string>) => void
): void

and consume the API in such way:

readFile('./myfile', (e) =>
  pipe(
    e,
    match(
      (err) => `Error: ${err.message}`,
      (data) => `Data: ${data.trim()}`
    ),
    console.log
  )
)

Category theory

We have seen how a founding pillar of functional programming is composition.

And how do we solve problems? We decompose bigger problems into smaller problems. If the smaller problems are still too big, we decompose them further, and so on. Finally, we write code that solves all the small problems. And then comes the essence of programming: we compose those pieces of code to create solutions to larger problems. Decomposition wouldn't make sense if we weren't able to put the pieces back together. - Bartosz Milewski

But what does it means exactly? How can we state whether two things compose? And how can we say if two things compose well?

Entities are composable if we can easily and generally combine their behaviours in some way without having to modify the entities being combined. I think of composability as being the key ingredient necessary for achieving reuse, and for achieving a combinatorial expansion of what is succinctly expressible in a programming model. - Paul Chiusano

We've briefly mentioned how a program written in functional styles tends to resemble a pipeline:

const program = pipe(
  input,
  f1, // pure function
  f2, // pure function
  f3, // pure function
  ...
)

But how simple it is to code in such a style? Let's try:

import { pipe } from 'fp-ts/function'
import * as RA from 'fp-ts/ReadonlyArray'

const double = (n: number): number => n * 2

/**
 * Given a ReadonlyArray<number> the program doubles the first element and returns it
 */
const program = (input: ReadonlyArray<number>): number =>
  pipe(
    input,
    RA.head, // compilation error! Type 'Option<number>' is not assignable to type 'number'
    double
  )

Why do I get a compilation error? Because head and double do not compose.

head: (as: ReadonlyArray<number>) => Option<number>
double: (n: number) => number

head's codomain is not included in double's domain.

Looks like our goal to program using pure functions is over..Or is it?

We need to be able to refer to some rigorous theory, one able to answer such fundamental questions.

We need to refer to a formal definition of composability.

Luckily, for the last 70 years ago, a large number of researchers, members of the oldest and largest humanity's open source project (mathematics) occupied itself with developing a theory dedicated to composability: category theory, a branch of mathematics founded by Saunders Mac Lane along Samuel Eilenberg (1945).

Categories capture the essence of composition.

Saunders Mac Lane

(Saunders Mac Lane)

(Samuel Eilenberg)

We'll see in the following chapters how a category can form the basis for:

• a model for a generic programming language
• a model for the concept of composition

Definition

The definition of a category, even though it isn't really complex, is a bit long, thus I'll split it in two parts:

• the first is merely technical (we need to define its constituents)
• the second one will be more relevant to what we care for: a notion of composition

Part I (Constituents)

A category is a pair of (Objects, Morphisms) where:

• Objects is a collection of objects
• Morphisms is a collection of morphisms (also called "arrows") between objects

Note. The term "object" has nothing to do with the concept of "objects" in programming. Just think about those "objects" as black boxes we can't inspect, or simple placeholders useful to define the various morphisms.

Every morphism f owns a source object A and a target object B.

In every morphism, both A and B are members of Objects. We write f: A ⟼ B and we say that "f is a morphism from A to B".

Note. For simplicity, from now on, I'll use labels only for objects, skipping the circles.

Part II (Composition)

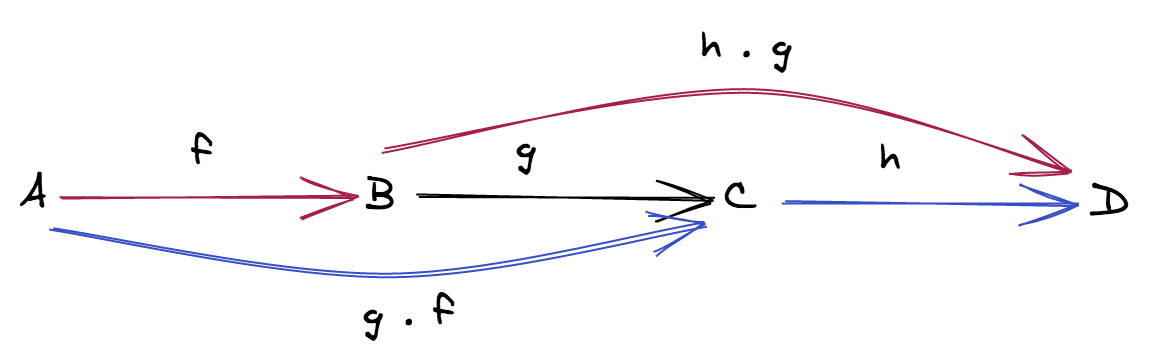
There is an operation, ∘, called "composition", such as the following properties hold true:

• (composition of morphisms) every time we have two morphisms f: A ⟼ B and g: B ⟼ C in Morphisms then there has to be a third morphism g ∘ f: A ⟼ C in Morphisms which is the composition of f and g

• (associativity) if f: A ⟼ B, g: B ⟼ C and h: C ⟼ D then h ∘ (g ∘ f) = (h ∘ g) ∘ f

• (identity) for every object X, there is a morphism identity: X ⟼ X called identity morphism of X, such as for every morphism f: A ⟼ X and g: X ⟼ B, the following equation holds true identity ∘ f = f and g ∘ identity = g.

Example

This category is very simple, there are three objects and six morphisms (1_A, 1_B, 1_C are the identity morphisms for A, B, C).

Modeling programming languages with categories

A category can be seen as a simplified model for a typed programming language, where:

• objects are types
• morphisms are functions
• ∘ is the usual function composition

The following diagram:

can be seen as an imaginary (and simple) programming language with just three types and six functions

Example given:

• A = string
• B = number
• C = boolean
• f = string => number
• g = number => boolean
• g ∘ f = string => boolean

The implementation could be something like:

const idA = (s: string): string => s

const idB = (n: number): number => n

const idC = (b: boolean): boolean => b

const f = (s: string): number => s.length

const g = (n: number): boolean => n > 2

// gf = g ∘ f
const gf = (s: string): boolean => g(f(s))

A category for TypeScript

We can define a category, let's call it TS, as a simplified model of the TypeScript language, where:

• objects are all the possible TypeScript types: string, number, ReadonlyArray<string>, etc...
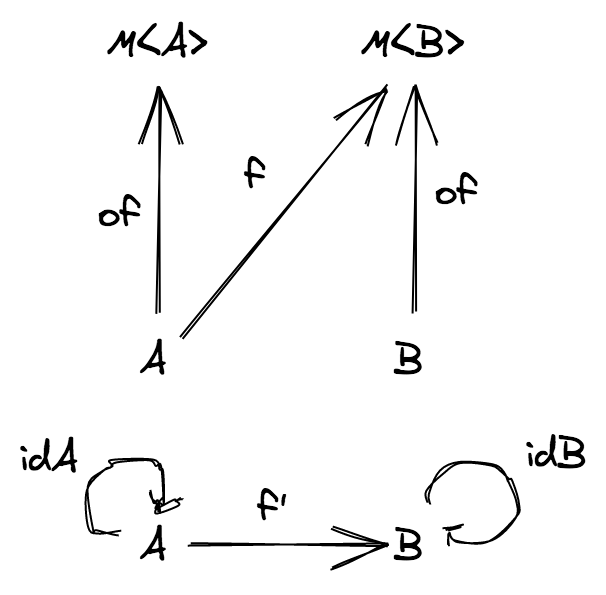
• morphisms are all TypeScript functions: (a: A) => B, (b: B) => C, ... where A, B, C, ... are TypeScript types
• the identity morphisms are all encoded in a single polymorphic function const identity = <A>(a: A): A => a
• morphism's composition is the usual function composition (which we know to be associative)

As a model of TypeScript, the TS category may seem a bit limited: no loops, no ifs, there's almost nothing... that being said that simplified model is rich enough to help us reach our goal: to reason about a well-defined notion of composition.

Composition's core problem

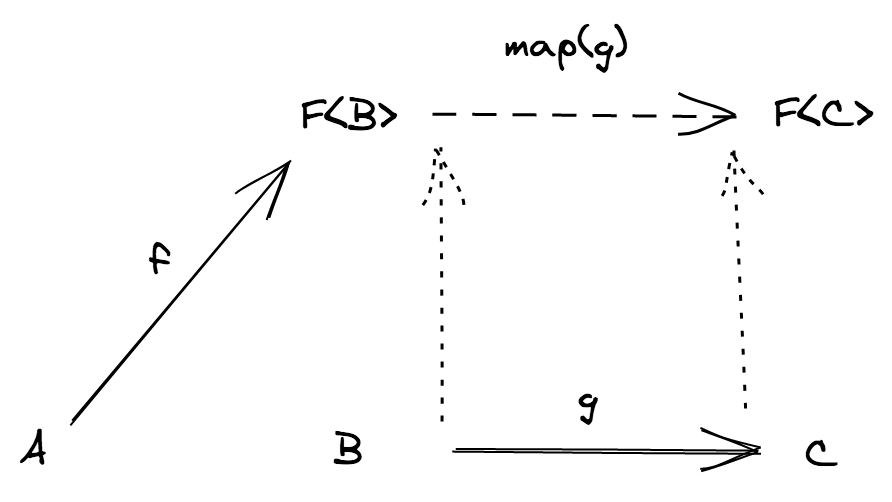
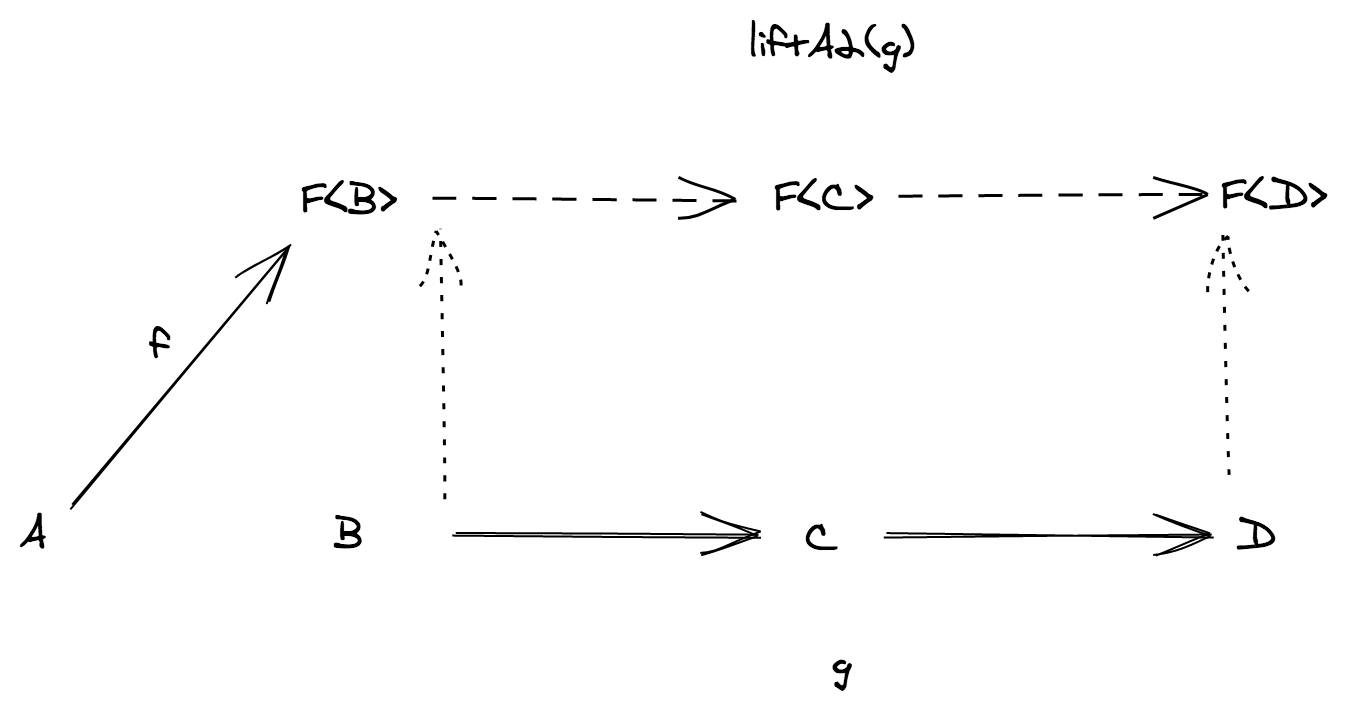
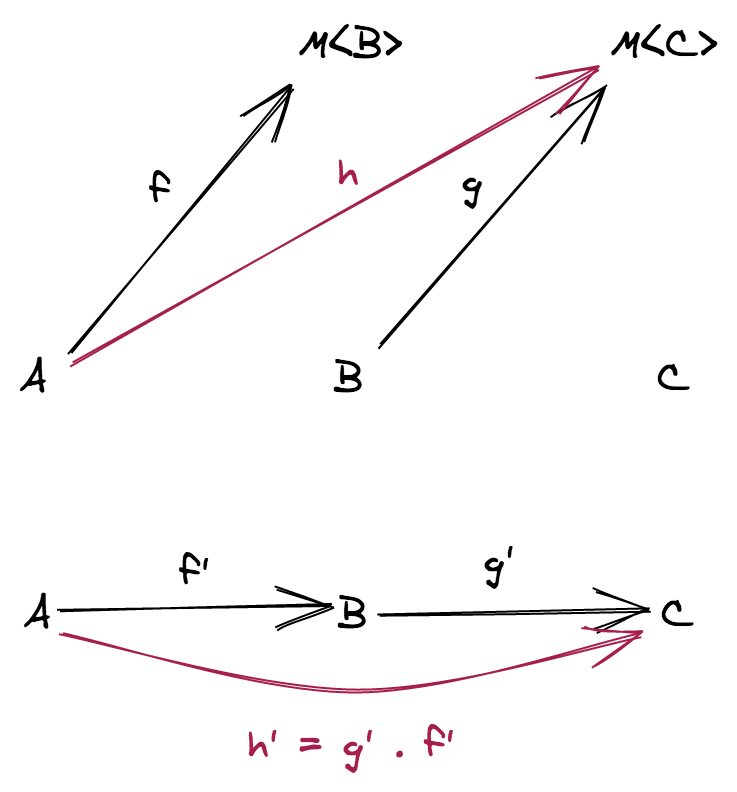
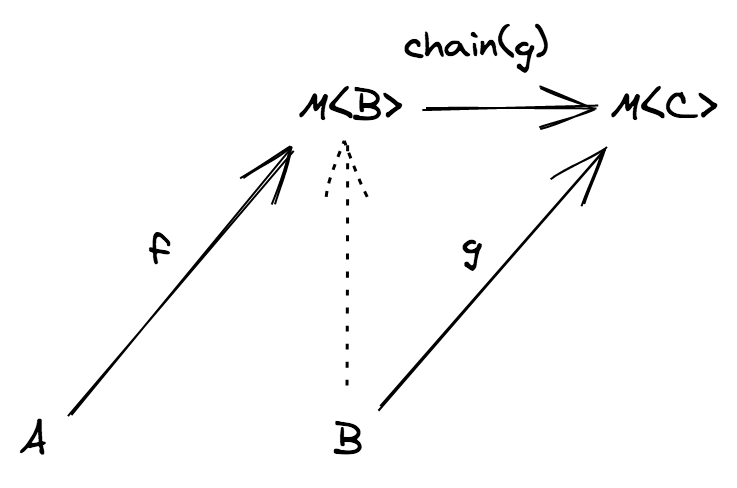
In the TS category we can compose two generic functions f: (a: A) => B and g: (c: C) => D as long as C = B

function flow<A, B, C>(f: (a: A) => B, g: (b: B) => C): (a: A) => C {
  return (a) => g(f(a))
}

function pipe<A, B, C>(a: A, f: (a: A) => B, g: (b: B) => C): C {
  return flow(f, g)(a)
}

But what happens if B != C? How can we compose two such functions? Should we give up?

In the next section we'll see under which conditions such a composition is possible.

Spoiler

• to compose f: (a: A) => B with g: (b: B) => C we use our usual function composition
• to compose f: (a: A) => F<B> with g: (b: B) => C we need a functor instance for F
• to compose f: (a: A) => F<B> with g: (b: B, c: C) => D we need an applicative functor instance for F
• to compose f: (a: A) => F<B> with g: (b: B) => F<C> we need a monad instance for F

The problem we started with at the beginning of this chapter corresponds to the second situation, where F is the Option type:

// A = ReadonlyArray<number>, B = number, F = Option
head: (as: ReadonlyArray<number>) => Option<number>
double: (n: number) => number

To solve it, the next chapter will talk about functors.

Functors

In the last section we've spoken about the TS category (the TypeScript category) and about function composition's core problem:

How can we compose two generic functions f: (a: A) => B and g: (c: C) => D?

Why is finding solutions to this problem so important?

Because, if it is true that categories can be used to model programming languages, morphisms (functions in the TS category) can be used to model programs.

Thus, solving this abstract problem means finding a concrete way of composing programs in a generic way. And that is really interesting for us developers, isn't it?

Functions as programs

If we want to model programs with functions we need to tackle an issue immediately:

How is it possible to model a program that produces side effects with a pure function?

The answer is to model side effects through effects, meaning types that represent side effects.

Let's see two possible techniques to do so in JavaScript:

• define a DSL (domain specific language) for effects
• use a thunk

The first technique, using a DSL, means modifying a program like:

function log(message: string): void {
  console.log(message) // side effect
}

changing its codomain to make the function return a description of the side effect:

type DSL = ... // sum type of every possible effect handled by the system

function log(message: string): DSL {
  return {
    type: "log",
    message
  }
}

Quiz. Is the freshly defined log function really pure? Actually log('foo') !== log('foo')!

This technique requires a way to combine effects and the definition of an interpreter able to execute the side effects when launching the final program.

The second technique, way simpler in TypeScript, is to enclose the computation in a thunk:

// a thunk representing a synchronous side effect
type IO<A> = () => A

const log = (message: string): IO<void> => {
  return () => console.log(message) // returns a thunk
}

The log program, once executed, won't cause immediately a side effect, but returns a value representing the computation (also known as action).

import { IO } from 'fp-ts/IO'

export const log = (message: string): IO<void> => {
  return () => console.log(message) // returns a thunk
}

export const main = log('hello!')
// there's nothing in the output at this point
// because `main` is only an inert value
// representing the computation

main()
// only when launching the program I will see the result

In functional programming there's a tendency to shove side effects (under the form of effects) to the border of the system (the main function) where they are executed by an interpreter obtaining the following schema:

system = pure core + imperative shell

In purely functional languages (like Haskell, PureScript or Elm) this division is strict and clear and imposed by the very languages.

Even with this thunk technique (the same technique used in fp-ts) we need a way to combine effects, which brings us back to our goal of composing programs in a generic way, let's see how.

We first need a bit of (informal) terminology: we'll call pure program a function with the following signature:

(a: A) => B

Such a signature models a program that takes an input of type A and returns a result of type B without any effect.

Example

The len program:

const len = (s: string): number => s.length

We'll call an effectful program a function with the following signature:

(a: A) => F<B>

Such a signature models a program that takes an input of type A and returns a result of type B together with an effect F, where F is some sort of type constructor.

Let's recall that a type constructor is an n-ary type operator that takes as argument one or more types and returns another type. We have seen examples of such constructors as Option, ReadonlyArray, Either.

Example

The head program:

import { Option, some, none } from 'fp-ts/Option'

const head = <A>(as: ReadonlyArray<A>): Option<A> =>
  as.length === 0 ? none : some(as[0])

is a program with an Option effect.

When we talk about effects we are interested in n-ary type constructors where n >= 1, example given:

Type constructor	Effect (interpretation)
ReadonlyArray<A>	a non deterministic computation
Option<A>	a computation that may fail
Either<E, A>	a computation that may fail
IO<A>	a synchronous computation that never fails
Task<A>	an asynchronous computation never fails
Reader<R, A>	reading from an environment

where

// a thunk returning a `Promise`
type Task<A> = () => Promise<A>

// `R` represents an "environment" needed for the computation
// (we can "read" from it) and `A` is the result
type Reader<R, A> = (r: R) => A

Let's get back to our core problem:

How do we compose two generic functions f: (a: A) => B e g: (c: C) => D?

With our current set of rules this general problem is not solvable. We need to add some boundaries to B and C.

We already know that if B = C then the solution is the usual function composition.

function flow<A, B, C>(f: (a: A) => B, g: (b: B) => C): (a: A) => C {
  return (a) => g(f(a))
}

But what about other cases?

A boundary that leads to functors

Let's consider the following boundary: B = F<C> for some type constructor F, we have the following situation:

• f: (a: A) => F<B> is an effectful program
• g: (b: B) => C is a pure program

In order to compose f with g we need to find a procedure that allows us to derive a function g from a function (b: B) => C to a function (fb: F<B>) => F<C> in order to use the usual function composition (this way the codomain of f would be the same of the new function's domain).

We have mutated the original problem in a new one: can we find a function, let's call it map, that operates this way?

Let's see some practical example:

Example (F = ReadonlyArray)

import { flow, pipe } from 'fp-ts/function'

// transforms functions `B -> C` to functions `ReadonlyArray<B> -> ReadonlyArray<C>`
const map = <B, C>(g: (b: B) => C) => (
  fb: ReadonlyArray<B>
): ReadonlyArray<C> => fb.map(g)

// -------------------
// usage example
// -------------------

interface User {
  readonly id: number
  readonly name: string
  readonly followers: ReadonlyArray<User>
}

const getFollowers = (user: User): ReadonlyArray<User> => user.followers
const getName = (user: User): string => user.name

// getFollowersNames: User -> ReadonlyArray<string>
const getFollowersNames = flow(getFollowers, map(getName))

// let's use `pipe` instead of `flow`...
export const getFollowersNames2 = (user: User) =>
  pipe(user, getFollowers, map(getName))

const user: User = {
  id: 1,
  name: 'Ruth R. Gonzalez',
  followers: [
    { id: 2, name: 'Terry R. Emerson', followers: [] },
    { id: 3, name: 'Marsha J. Joslyn', followers: [] }
  ]
}

console.log(getFollowersNames(user)) // => [ 'Terry R. Emerson', 'Marsha J. Joslyn' ]

Example (F = Option)

import { flow } from 'fp-ts/function'
import { none, Option, match, some } from 'fp-ts/Option'

// transforms functions `B -> C` to functions `Option<B> -> Option<C>`
const map = <B, C>(g: (b: B) => C): ((fb: Option<B>) => Option<C>) =>
  match(
    () => none,
    (b) => {
      const c = g(b)
      return some(c)
    }
  )

// -------------------
// usage example
// -------------------

import * as RA from 'fp-ts/ReadonlyArray'

const head: (input: ReadonlyArray<number>) => Option<number> = RA.head
const double = (n: number): number => n * 2

// getDoubleHead: ReadonlyArray<number> -> Option<number>
const getDoubleHead = flow(head, map(double))

console.log(getDoubleHead([1, 2, 3])) // => some(2)
console.log(getDoubleHead([])) // => none

Example (F = IO)

import { flow } from 'fp-ts/function'
import { IO } from 'fp-ts/IO'

// transforms functions `B -> C` to functions `IO<B> -> IO<C>`
const map = <B, C>(g: (b: B) => C) => (fb: IO<B>): IO<C> => () => {
  const b = fb()
  return g(b)
}

// -------------------
// usage example
// -------------------

interface User {
  readonly id: number
  readonly name: string
}

// a dummy in-memory database
const database: Record<number, User> = {
  1: { id: 1, name: 'Ruth R. Gonzalez' },
  2: { id: 2, name: 'Terry R. Emerson' },
  3: { id: 3, name: 'Marsha J. Joslyn' }
}

const getUser = (id: number): IO<User> => () => database[id]
const getName = (user: User): string => user.name

// getUserName: number -> IO<string>
const getUserName = flow(getUser, map(getName))

console.log(getUserName(1)()) // => Ruth R. Gonzalez

Example (F = Task)

import { flow } from 'fp-ts/function'
import { Task } from 'fp-ts/Task'

// transforms functions `B -> C` into functions `Task<B> -> Task<C>`
const map = <B, C>(g: (b: B) => C) => (fb: Task<B>): Task<C> => () => {
  const promise = fb()
  return promise.then(g)
}

// -------------------
// usage example
// -------------------

interface User {
  readonly id: number
  readonly name: string
}

// a dummy remote database
const database: Record<number, User> = {
  1: { id: 1, name: 'Ruth R. Gonzalez' },
  2: { id: 2, name: 'Terry R. Emerson' },
  3: { id: 3, name: 'Marsha J. Joslyn' }
}

const getUser = (id: number): Task<User> => () => Promise.resolve(database[id])
const getName = (user: User): string => user.name

// getUserName: number -> Task<string>
const getUserName = flow(getUser, map(getName))

getUserName(1)().then(console.log) // => Ruth R. Gonzalez

Example (F = Reader)

import { flow } from 'fp-ts/function'
import { Reader } from 'fp-ts/Reader'

// transforms functions `B -> C` into functions `Reader<R, B> -> Reader<R, C>`
const map = <B, C>(g: (b: B) => C) => <R>(fb: Reader<R, B>): Reader<R, C> => (
  r
) => {
  const b = fb(r)
  return g(b)
}

// -------------------
// usage example
// -------------------

interface User {
  readonly id: number
  readonly name: string
}

interface Env {
  // a dummy in-memory database
  readonly database: Record<string, User>
}

const getUser = (id: number): Reader<Env, User> => (env) => env.database[id]
const getName = (user: User): string => user.name

// getUserName: number -> Reader<Env, string>
const getUserName = flow(getUser, map(getName))

console.log(
  getUserName(1)({
    database: {
      1: { id: 1, name: 'Ruth R. Gonzalez' },
      2: { id: 2, name: 'Terry R. Emerson' },
      3: { id: 3, name: 'Marsha J. Joslyn' }
    }
  })
) // => Ruth R. Gonzalez

More generally, when a type constructor F admits a map function, we say it admits a functor instance.

From a mathematical point of view, functors are maps between categories that preserve the structure of the category, meaning they preserve the identity morphisms and the composition operation.

Since categories are pairs of objects and morphisms, a functor too is a pair of two things:

• a map between objects that binds every object X in C to an object in D.
• a map between morphisms that binds every morphism f in C to a morphism map(f) in D.

where C e D are two categories (aka two programming languages).

Even though a map between two different programming languages is a fascinating idea, we're more interested in a map where C and D are the same (the TS category). In that case we're talking about endofunctors (from the greek "endo" meaning "inside", "internal").

From now on, unless specified differently, when we write "functor" we mean an endofunctor in the TS category.

Now we know the practical side of functors, let's see the formal definition.

Definition

A functor is a pair (F, map) where:

• F is an n-ary (n >= 1) type constructor mapping every type X in a type F<X> (map between objects)
• map is a function with the following signature:

map: <A, B>(f: (a: A) => B) => ((fa: F<A>) => F<B>)

that maps every function f: (a: A) => B in a function map(f): (fa: F<A>) => F<B> (map between morphism)

The following properties have to hold true:

• map(1_X) = 1_F(X) (identities go to identities)
• map(g ∘ f) = map(g) ∘ map(f) (the image of a composition is the composition of its images)

The second law allows to refactor and optimize the following computation:

import { flow, increment, pipe } from 'fp-ts/function'
import { map } from 'fp-ts/ReadonlyArray'

const double = (n: number): number => n * 2

// iterates array twice
console.log(pipe([1, 2, 3], map(double), map(increment))) // => [ 3, 5, 7 ]

// single iteration
console.log(pipe([1, 2, 3], map(flow(double, increment)))) // => [ 3, 5, 7 ]

Functors and functional error handling

Functors have a positive impact on functional error handling, let's see a practical example:

declare const doSomethingWithIndex: (index: number) => string

export const program = (ns: ReadonlyArray<number>): string => {
  // -1 indicates that no element has been found
  const i = ns.findIndex((n) => n > 0)
  if (i !== -1) {
    return doSomethingWithIndex(i)
  }
  throw new Error('cannot find a positive number')
}

Using the native findIndex API we are forced to use an if branch to test whether we have a result different than -1. If we forget to do so, the value -1 could be unintentionally passed as input to doSomethingWithIndex.

Let's see how easier it is to obtain the same behavior using Option and its functor instance:

import { pipe } from 'fp-ts/function'
import { map, Option } from 'fp-ts/Option'
import { findIndex } from 'fp-ts/ReadonlyArray'

declare const doSomethingWithIndex: (index: number) => string

export const program = (ns: ReadonlyArray<number>): Option<string> =>
  pipe(
    ns,
    findIndex((n) => n > 0),
    map(doSomethingWithIndex)
  )

Practically, using Option, we're always in front of the happy path, error handing happens behind the scenes thanks to map.

데모 (optional)

04_functor.ts

Quiz. Task<A> represents an asynchronous call that always succeed, how can we model a computation that can fail instead?

Functors compose

Functors compose, meaning that given two functors F and G then the composition F<G<A>> is still a functor and the map of this composition is the composition of the maps.

Example (F = Task, G = Option)

import { flow } from 'fp-ts/function'
import * as O from 'fp-ts/Option'
import * as T from 'fp-ts/Task'

type TaskOption<A> = T.Task<O.Option<A>>

export const map: <A, B>(
  f: (a: A) => B
) => (fa: TaskOption<A>) => TaskOption<B> = flow(O.map, T.map)

// -------------------
// usage example
// -------------------

interface User {
  readonly id: number
  readonly name: string
}

// a dummy remote database
const database: Record<number, User> = {
  1: { id: 1, name: 'Ruth R. Gonzalez' },
  2: { id: 2, name: 'Terry R. Emerson' },
  3: { id: 3, name: 'Marsha J. Joslyn' }
}

const getUser = (id: number): TaskOption<User> => () =>
  Promise.resolve(O.fromNullable(database[id]))
const getName = (user: User): string => user.name

// getUserName: number -> TaskOption<string>
const getUserName = flow(getUser, map(getName))

getUserName(1)().then(console.log) // => some('Ruth R. Gonzalez')
getUserName(4)().then(console.log) // => none

Contravariant Functors

In the previous section we haven't been completely thorough with our definitions. What we have seen in the previous section and called "functors" should be more properly called covariant functors.

In this section we'll see another variant of the functor concept, contravariant functors.

The definition of a contravariant functor is pretty much the same of the covariant one, except for the signature of its fundamental operation, which is called contramap rather than map.

Example

import { map } from 'fp-ts/Option'
import { contramap } from 'fp-ts/Eq'

type User = {
  readonly id: number
  readonly name: string
}

const getId = (_: User): number => _.id

// the way `map` operates...
// const getIdOption: (fa: Option<User>) => Option<number>
const getIdOption = map(getId)

// the way `contramap` operates...
// const getIdEq: (fa: Eq<number>) => Eq<User>
const getIdEq = contramap(getId)

import * as N from 'fp-ts/number'

const EqID = getIdEq(N.Eq)

/*

In the `Eq` chapter we saw:

const EqID: Eq<User> = pipe(
  N.Eq,
  contramap((_: User) => _.id)
)
*/

Functors in fp-ts

How do we define a functor instance in fp-ts? Let's see some example.

The following interface represents the model of some result we get by calling some HTTP API:

interface Response<A> {
  url: string
  status: number
  headers: Record<string, string>
  body: A
}

Please note that since body is parametric, this makes Response a good candidate to find a functor instance given that Response is a an n-ary type constructor with n >= 1 (a necessary condition).

To define a functor instance for Response we need to define a map function along some technical details required by fp-ts.

// `Response.ts` module

import { pipe } from 'fp-ts/function'
import { Functor1 } from 'fp-ts/Functor'

declare module 'fp-ts/HKT' {
  interface URItoKind<A> {
    readonly Response: Response<A>
  }
}

export interface Response<A> {
  readonly url: string
  readonly status: number
  readonly headers: Record<string, string>
  readonly body: A
}

export const map = <A, B>(f: (a: A) => B) => (
  fa: Response<A>
): Response<B> => ({
  ...fa,
  body: f(fa.body)
})

// functor instance for `Response<A>`
export const Functor: Functor1<'Response'> = {
  URI: 'Response',
  map: (fa, f) => pipe(fa, map(f))
}

Do functors solve the general problem?

Not yet. Functors allow us to compose an effectful program f with a pure program g, but g has to be a unary function, accepting one single argument. What happens if g takes two or more arguments?

Program f	Program g	Composition
pure	pure	g ∘ f
effectful	pure (unary)	map(g) ∘ f
effectful	pure (n-ary, n > 1)	?

To manage this circumstance we need something more, in the next chapter we'll see another important abstraction in functional programming: applicative functors.

Applicative functors

In the section regarding functors we've seen that we can compose an effectful program f: (a: A) => F<B> with a pure one g: (b: B) => C through the transformation of g to a function map(g): (fb: F<B>) => F<C> (if and only if F admits a functor instance).

Program f	Program g	Composition
pure	pure	g ∘ f
effectful	pure (unary)	map(g) ∘ f

But g has to be unary, it can only accept a single argument as input. What happens if g accepts two arguments? Can we still transform g using only the functor instance?

Currying

First of all we need to model a function that accepts two arguments of type B and C (we can use a tuple for this) and returns a value of type D:

g: (b: B, c: C) => D

We can rewrite g using a technique called currying.

Currying is the technique of translating the evaluation of a function that takes multiple arguments into evaluating a sequence of functions, each with a single argument. For example, a function that takes two arguments, one from B and one from C, and produces outputs in D, by currying is translated into a function that takes a single argument from C and produces as outputs functions from B to C.

(source: currying on wikipedia.org)

Thus, through currying, we can rewrite g as:

g: (b: B) => (c: C) => D

Example

interface User {
  readonly id: number
  readonly name: string
  readonly followers: ReadonlyArray<User>
}

const addFollower = (follower: User, user: User): User => ({
  ...user,
  followers: [...user.followers, follower]
})

Let's refactor addFollower through currying

interface User {
  readonly id: number
  readonly name: string
  readonly followers: ReadonlyArray<User>
}

const addFollower = (follower: User) => (user: User): User => ({
  ...user,
  followers: [...user.followers, follower]
})

// -------------------
// usage example
// -------------------

const user: User = { id: 1, name: 'Ruth R. Gonzalez', followers: [] }
const follower: User = { id: 3, name: 'Marsha J. Joslyn', followers: [] }

console.log(addFollower(follower)(user))
/*
{
  id: 1,
  name: 'Ruth R. Gonzalez',
  followers: [ { id: 3, name: 'Marsha J. Joslyn', followers: [] } ]
}
*/

The ap operation

Suppose that:

• we do not have a follower but only his id
• we do not have a user but only his id
• that we have an API fetchUser which, given an id, queries an endpoint that returns the corresponding User

import * as T from 'fp-ts/Task'

interface User {
  readonly id: number
  readonly name: string
  readonly followers: ReadonlyArray<User>
}

const addFollower = (follower: User) => (user: User): User => ({
  ...user,
  followers: [...user.followers, follower]
})

declare const fetchUser: (id: number) => T.Task<User>

const userId = 1
const followerId = 3

const result = addFollower(fetchUser(followerId))(fetchUser(userId)) // does not compile

I can't use addFollower anymore! How can we proceed?

If only we had a function with the following signature:

declare const addFollowerAsync: (
  follower: T.Task<User>
) => (user: T.Task<User>) => T.Task<User>

we could proceed with ease:

import * as T from 'fp-ts/Task'

interface User {
  readonly id: number
  readonly name: string
  readonly followers: ReadonlyArray<User>
}

declare const fetchUser: (id: number) => T.Task<User>

declare const addFollowerAsync: (
  follower: T.Task<User>
) => (user: T.Task<User>) => T.Task<User>

const userId = 1
const followerId = 3

// const result: T.Task<User>
const result = addFollowerAsync(fetchUser(followerId))(fetchUser(userId)) // now compiles

We can obviously implement addFollowerAsync manually, but is it possible instead to find a transformation which starting with a function like addFollower: (follower: User) => (user: User): User returns a function like addFollowerAsync: (follower: Task<User>) => (user: Task<User>) => Task<User>?

More generally what we would like to have is a transformation, call it liftA2, which beginning with a function g: (b: B) => (c: C) => D returns a function with the following signature:

liftA2(g): (fb: F<B>) => (fc: F<C>) => F<D>

How can we obtain it? Given that g is now a unary function, we can leverage the functor instance and the good old map:

map(g): (fb: F<B>) => F<(c: C) => D>

Now we are blocked: there's no legal operation the functor instance provides us to "unpack" the type F<(c: C) => D> into (fc: F<C>) => F<D>.

We need to introduce a new operation ap which realizes this unpacking:

declare const ap: <A>(fa: Task<A>) => <B>(fab: Task<(a: A) => B>) => Task<B>

Note. Why is it names "ap"? Because it can be seen like some sort of function application.

// `apply` applies a function to a value
declare const apply: <A>(a: A) => <B>(f: (a: A) => B) => B

declare const ap: <A>(a: Task<A>) => <B>(f: Task<(a: A) => B>) => Task<B>
// `ap` applies a function wrapped into an effect to a value wrapped into an effect

Now that we have ap we can define liftA2:

import { pipe } from 'fp-ts/function'
import * as T from 'fp-ts/Task'

const liftA2 = <B, C, D>(g: (b: B) => (c: C) => D) => (fb: T.Task<B>) => (
  fc: T.Task<C>
): T.Task<D> => pipe(fb, T.map(g), T.ap(fc))

interface User {
  readonly id: number
  readonly name: string
  readonly followers: ReadonlyArray<User>
}

const addFollower = (follower: User) => (user: User): User => ({
  ...user,
  followers: [...user.followers, follower]
})

// const addFollowerAsync: (fb: T.Task<User>) => (fc: T.Task<User>) => T.Task<User>
const addFollowerAsync = liftA2(addFollower)

and finally, we can compose fetchUser with the previous result:

import { flow, pipe } from 'fp-ts/function'
import * as T from 'fp-ts/Task'

const liftA2 = <B, C, D>(g: (b: B) => (c: C) => D) => (fb: T.Task<B>) => (
  fc: T.Task<C>
): T.Task<D> => pipe(fb, T.map(g), T.ap(fc))

interface User {
  readonly id: number
  readonly name: string
  readonly followers: ReadonlyArray<User>
}

const addFollower = (follower: User) => (user: User): User => ({
  ...user,
  followers: [...user.followers, follower]
})

declare const fetchUser: (id: number) => T.Task<User>

// const program: (id: number) => (fc: T.Task<User>) => T.Task<User>
const program = flow(fetchUser, liftA2(addFollower))

const userId = 1
const followerId = 3

// const result: T.Task<User>
const result = program(followerId)(fetchUser(userId))

We have found a standard procedure to compose two functions f: (a: A) => F<B>, g: (b: B, c: C) => D:

1. we transform g through currying in a function g: (b: B) => (c: C) => D
2. we define the ap function for the effect F (library function)
3. we define the utility function liftA2 for the effect F (library function)
4. we obtain the composition flow(f, liftA2(g))

Let's see how's the ap operation implemented for some of the type constructors we've already seen:

Example (F = ReadonlyArray)

import { increment, pipe } from 'fp-ts/function'

const ap = <A>(fa: ReadonlyArray<A>) => <B>(
  fab: ReadonlyArray<(a: A) => B>
): ReadonlyArray<B> => {
  const out: Array<B> = []
  for (const f of fab) {
    for (const a of fa) {
      out.push(f(a))
    }
  }
  return out
}

const double = (n: number): number => n * 2

pipe([double, increment], ap([1, 2, 3]), console.log) // => [ 2, 4, 6, 2, 3, 4 ]

Example (F = Option)

import { pipe } from 'fp-ts/function'
import * as O from 'fp-ts/Option'

const ap = <A>(fa: O.Option<A>) => <B>(
  fab: O.Option<(a: A) => B>
): O.Option<B> =>
  pipe(
    fab,
    O.match(
      () => O.none,
      (f) =>
        pipe(
          fa,
          O.match(
            () => O.none,
            (a) => O.some(f(a))
          )
        )
    )
  )

const double = (n: number): number => n * 2

pipe(O.some(double), ap(O.some(1)), console.log) // => some(2)
pipe(O.some(double), ap(O.none), console.log) // => none
pipe(O.none, ap(O.some(1)), console.log) // => none
pipe(O.none, ap(O.none), console.log) // => none

Example (F = IO)

import { IO } from 'fp-ts/IO'

const ap = <A>(fa: IO<A>) => <B>(fab: IO<(a: A) => B>): IO<B> => () => {
  const f = fab()
  const a = fa()
  return f(a)
}

Example (F = Task)

import { Task } from 'fp-ts/Task'

const ap = <A>(fa: Task<A>) => <B>(fab: Task<(a: A) => B>): Task<B> => () =>
  Promise.all([fab(), fa()]).then(([f, a]) => f(a))

Example (F = Reader)

import { Reader } from 'fp-ts/Reader'

const ap = <R, A>(fa: Reader<R, A>) => <B>(
  fab: Reader<R, (a: A) => B>
): Reader<R, B> => (r) => {
  const f = fab(r)
  const a = fa(r)
  return f(a)
}

We've seen how with ap we can manage functions with two parameters, but what happens with functions that take three parameters? Do we need yet another abstraction?

Good news is no, map and ap are sufficient:

import { pipe } from 'fp-ts/function'
import * as T from 'fp-ts/Task'

const liftA3 = <B, C, D, E>(f: (b: B) => (c: C) => (d: D) => E) => (
  fb: T.Task<B>
) => (fc: T.Task<C>) => (fd: T.Task<D>): T.Task<E> =>
  pipe(fb, T.map(f), T.ap(fc), T.ap(fd))

const liftA4 = <B, C, D, E, F>(
  f: (b: B) => (c: C) => (d: D) => (e: E) => F
) => (fb: T.Task<B>) => (fc: T.Task<C>) => (fd: T.Task<D>) => (
  fe: T.Task<E>
): T.Task<F> => pipe(fb, T.map(f), T.ap(fc), T.ap(fd), T.ap(fe))

// etc...

Now we cam update ore "composition table":

Program f	Program g	Composition
pure	pure	g ∘ f
effectful	pure (unary)	map(g) ∘ f
effectful	pure, n-ary	liftAn(g) ∘ f

The of operation

Now we know that given two function f: (a: A) => F<B>, g: (b: B, c: C) => D we can obtain the composition h:

h: (a: A) => (fc: F<C>) => F<D>

To execute h we need a new value of type A and a value of type F<C>.

But what happens if, instead of having a value of type F<C>, for the second parameter fc we only have a value of type C?

It would be helpful to have an operation which can transform a value of type C in a value of type F<C> in order to use h.

Let's introduce such operation, called of (other synonyms: pure, return):

declare const of: <C>(c: C) => F<C>

In literature the term applicative functors is used for the type constructors which admith both the ap and of operations.

Let's see how of is defined for some type constructors we've already seen:

Example (F = ReadonlyArray)

const of = <A>(a: A): ReadonlyArray<A> => [a]

Example (F = Option)

import * as O from 'fp-ts/Option'

const of = <A>(a: A): O.Option<A> => O.some(a)

Example (F = IO)

import { IO } from 'fp-ts/IO'

const of = <A>(a: A): IO<A> => () => a

Example (F = Task)

import { Task } from 'fp-ts/Task'

const of = <A>(a: A): Task<A> => () => Promise.resolve(a)

Example (F = Reader)

import { Reader } from 'fp-ts/Reader'

const of = <R, A>(a: A): Reader<R, A> => () => a

데모

05_applicative.ts

Applicative functors compose

Applicative functors compose, meaning that given two applicative functors F and G, their composition F<G<A>> is still an applicative functor.

Example (F = Task, G = Option)

The of of the composition is the composition of the ofs:

import { flow } from 'fp-ts/function'
import * as O from 'fp-ts/Option'
import * as T from 'fp-ts/Task'

type TaskOption<A> = T.Task<O.Option<A>>

const of: <A>(a: A) => TaskOption<A> = flow(O.of, T.of)

the ap of the composition is obtained by the following pattern:

const ap = <A>(
  fa: TaskOption<A>
): (<B>(fab: TaskOption<(a: A) => B>) => TaskOption<B>) =>
  flow(
    T.map((gab) => (ga: O.Option<A>) => O.ap(ga)(gab)),
    T.ap(fa)
  )

Do applicative functors solve the general problem?

Not yet. There's one last very important case to consider: when both programs are effectful.

Yet again we need something more, in the following chapter we'll talk about one of the most important abstractions in functional programming: monads.

Monads

(Eugenio Moggi is a professor of computer science at the University of Genoa, Italy. He first described the general use of monads to structure programs)

(Philip Lee Wadler is an American computer scientist known for his contributions to programming language design and type theory)

In the last chapter we have seen how we can compose an effectful program f: (a: A) => F<B> with an n-ary pure program g, if and only if the type constructor F admits an applicative functor instance:

Program f	Program g	Composition
pure	pure	g ∘ f
effectful	pure (unary)	map(g) ∘ f
effectful	pure, n-ary	liftAn(g) ∘ f

But we need to solve one last, quite common, case: when both programs are effectful:

f: (a: A) => F<B>
g: (b: B) => F<C>

What is the composition of f and g?

The problem with nested contexts

Let's see few examples on why we need something more.

Example (F = Array)

Suppose we want to get followers' followers.

import { pipe } from 'fp-ts/function'
import * as A from 'fp-ts/ReadonlyArray'

interface User {
  readonly id: number
  readonly name: string
  readonly followers: ReadonlyArray<User>
}

const getFollowers = (user: User): ReadonlyArray<User> => user.followers

declare const user: User

// followersOfFollowers: ReadonlyArray<ReadonlyArray<User>>
const followersOfFollowers = pipe(user, getFollowers, A.map(getFollowers))

There's something wrong here, followersOfFollowers has a type ReadonlyArray<ReadonlyArray<User>> but we want ReadonlyArray<User>.

We need to flatten nested arrays.

The function flatten: <A>(mma: ReadonlyArray<ReadonlyArray<A>>) => ReadonlyArray<A> exported by the fp-ts/ReadonlyArray is exactly what we need:

// followersOfFollowers: ReadonlyArray<User>
const followersOfFollowers = pipe(
  user,
  getFollowers,
  A.map(getFollowers),
  A.flatten
)

Cool! Let's see some other data type.

Example (F = Option) Suppose you want to calculate the reciprocal of the first element of a numerical array:

import { pipe } from 'fp-ts/function'
import * as O from 'fp-ts/Option'
import * as A from 'fp-ts/ReadonlyArray'

const inverse = (n: number): O.Option<number> =>
  n === 0 ? O.none : O.some(1 / n)

// inverseHead: O.Option<O.Option<number>>
const inverseHead = pipe([1, 2, 3], A.head, O.map(inverse))

Oops, it happened again, inverseHead has type Option<Option<number>> but we want Option<number>.

We need to flatten again the nested Options.

The flatten: <A>(mma: Option<Option<A>>) => Option<A> function exported by the fp-ts/Option module is what we need:

// inverseHead: O.Option<number>
const inverseHead = pipe([1, 2, 3], A.head, O.map(inverse), O.flatten)

All of those flatten funcitons...They aren't a coincidence, there is a functional pattern behind the scenes: both the type constructors ReadonlyArray and Option (and many others) admit a monad instance and

flatten is the most peculiar operation of monads

Note. A common synonym of flatten is join.

So, what is a monad?

Here is how they are often presented...

Monad Definition

Definition. A monad is defined by three things:

(1) a type constructor M admitting a functor instance

(2) a function of (also called pure or return) with the following signature:

of: <A>(a: A) => M<A>

(3) a chain function (also called flatMap or bind) with the following signature:

chain: <A, B>(f: (a: A) => M<B>) => (ma: M<A>) => M<B>

The of and chain functions need to obey three laws:

• chain(of) ∘ f = f (Left identity)
• chain(f) ∘ of = f (Right identity)
• chain(h) ∘ (chain(g) ∘ f) = chain((chain(h) ∘ g)) ∘ f (Associativity)

where f, g, h are all effectful functions and ∘ is the usual function composition.

When I saw this definition for the first time I had many questions:

• why exactly those two operation of and chain? and why to they have those signatures?
• why do they have those synonyms like "pure" or "flatMap"?
• why does laws need to hold true? What do they mean?
• if flatten is so important for monads, why it doesn't compare in its definition?

This chapter will try to answer all of these questions.

Let's get back to the core problem: what is the composition of two effectful functions f and g?

(two Kleisli Arrows)

Note. An effectful function is also called Kleisli arrow.

For the time being I don't even know the type of such composition.

But we've already seen some abstractions that talks specifically about composition. Do you remember what we said about categories?

Categories capture the essence of composition

We can transform our problem into a category problem, meaning: can we find a category that models the composition of Kleisli arrows?

The Kleisli category

(Heinrich Kleisli, Swiss mathematician)

Let's try building a category K (called Kleisli category) which contains only Kleisli arrows:

• objects will be the same objects of the TS category, so all TypeScript types.
• morphisms are built like this: every time there is a Kleisli arrow f: A ⟼ M<B> in TS we draw an arrow f': A ⟼ B in K

(above the composition in the TS category, below the composition in the K construction)

So what would be the composition of f and g in K? It's th red arrow called h' in the image below:

(above the composition in the TS category, below the composition in the K construction)

Given that h' is an arrow from A to C in K, we can find a corresponding function h from A to M<C> in TS.

Thus, a good candidate for the following composition of f and g in TS is still a Kleisli arrow with the following signature: (a: A) => M<C>.

Let's try implementing such a function.

Defining chain step by step

The first point (1) of the monad definition tells us that M admits a functor instance, thus we can use the map function to transform the function g: (b: B) => M<C> into a function map(g): (mb: M<B>) => M<M<C>>

(how to obtain the h function)

We're stuck now though: there is no legal operation for the functor instance that allows us to flatten a value of type M<M<C>> into a value of type M<C>, we need an additional operation, let's call it flatten.

If we can define such operation then we can find the composition we were looking for:

h = flatten ∘ map(g) ∘ f

By joining the flatten ∘ map(g) names we get "flatMap", hence the name!

Thus we can get chain in this way

chain = flatten ∘ map(g)

(how chain operates on the function g)

Now we can update our composition table

Program f	Program g	Composition
pure	pure	g ∘ f
effectful	pure (unary)	map(g) ∘ f
effectful	pure, n-ary	liftAn(g) ∘ f
effectful	effectful	chain(g) ∘ f

What about of? Well, of comes from the identity morphisms in K: for every identity morphism 1_A in K there has to be a corresponding function from A to M<A> (that is, of: <A>(a: A) => M<A>).

(where of comes from)

The fact that of is the neutral element for chain allows this kind of flux control (pretty common):

pipe(
  mb,
  M.chain((b) => (predicate(b) ? M.of(b) : g(b)))
)

where predicate: (b: B) => boolean, mb: M<B> and g: (b: B) => M<B>.

Last question: where do the laws come from? They are nothing else but the categorical laws in K translated to TS:

Law	K	TS
Left identity	1B ∘ f' = f'	chain(of) ∘ f = f
Right identity	f' ∘ 1A = f'	chain(f) ∘ of = f
Associativity	h' ∘ (g' ∘ f') = (h' ∘ g') ∘ f'	chain(h) ∘ (chain(g) ∘ f) = chain((chain(h) ∘ g)) ∘ f

If we now go back to the examples that showed the problem with nested contexts we can solve them using chain:

import { pipe } from 'fp-ts/function'
import * as O from 'fp-ts/Option'
import * as A from 'fp-ts/ReadonlyArray'

interface User {
  readonly id: number
  readonly name: string
  readonly followers: ReadonlyArray<User>
}

const getFollowers = (user: User): ReadonlyArray<User> => user.followers

declare const user: User

const followersOfFollowers: ReadonlyArray<User> = pipe(
  user,
  getFollowers,
  A.chain(getFollowers)
)

const inverse = (n: number): O.Option<number> =>
  n === 0 ? O.none : O.some(1 / n)

const inverseHead: O.Option<number> = pipe([1, 2, 3], A.head, O.chain(inverse))

Let's see how chain is implemented for the usual type constructors we've already seen:

Example (F = ReadonlyArray)

// transforms functions `B -> ReadonlyArray<C>` into functions `ReadonlyArray<B> -> ReadonlyArray<C>`
const chain = <B, C>(g: (b: B) => ReadonlyArray<C>) => (
  mb: ReadonlyArray<B>
): ReadonlyArray<C> => {
  const out: Array<C> = []
  for (const b of mb) {
    out.push(...g(b))
  }
  return out
}

Example (F = Option)

import { match, none, Option } from 'fp-ts/Option'

// transforms functions `B -> Option<C>` into functions `Option<B> -> Option<C>`
const chain = <B, C>(g: (b: B) => Option<C>): ((mb: Option<B>) => Option<C>) =>
  match(() => none, g)

Example (F = IO)

import { IO } from 'fp-ts/IO'

// transforms functions `B -> IO<C>` into functions `IO<B> -> IO<C>`
const chain = <B, C>(g: (b: B) => IO<C>) => (mb: IO<B>): IO<C> => () =>
  g(mb())()

Example (F = Task)

import { Task } from 'fp-ts/Task'

// transforms functions `B -> Task<C>` into functions `Task<B> -> Task<C>`
const chain = <B, C>(g: (b: B) => Task<C>) => (mb: Task<B>): Task<C> => () =>
  mb().then((b) => g(b)())

Example (F = Reader)

import { Reader } from 'fp-ts/Reader'

// transforms functions `B -> Reader<R, C>` into functions `Reader<R, B> -> Reader<R, C>`
const chain = <B, R, C>(g: (b: B) => Reader<R, C>) => (
  mb: Reader<R, B>
): Reader<R, C> => (r) => g(mb(r))(r)

Manipulating programs

Let's see now, how thanks to referential transparency and the monad concept we can programmaticaly manipulate programs.

Here's a small program that reads / writes a file:

import { log } from 'fp-ts/Console'
import { IO, chain } from 'fp-ts/IO'
import { pipe } from 'fp-ts/function'
import * as fs from 'fs'

// -----------------------------------------
// library functions
// -----------------------------------------

const readFile = (filename: string): IO<string> => () =>
  fs.readFileSync(filename, 'utf-8')

const writeFile = (filename: string, data: string): IO<void> => () =>
  fs.writeFileSync(filename, data, { encoding: 'utf-8' })

// API derived from the previous functions
const modifyFile = (filename: string, f: (s: string) => string): IO<void> =>
  pipe(
    readFile(filename),
    chain((s) => writeFile(filename, f(s)))
  )

// -----------------------------------------
// program
// -----------------------------------------

const program1 = pipe(
  readFile('file.txt'),
  chain(log),
  chain(() => modifyFile('file.txt', (s) => s + '\n// eof')),
  chain(() => readFile('file.txt')),
  chain(log)
)

The actions:

pipe(readFile('file.txt'), chain(log))

is repeated more than once in the program, but given that referential transparency holds we can factor it and assign it to a constant:

const read = pipe(readFile('file.txt'), chain(log))
const modify = modifyFile('file.txt', (s) => s + '\n// eof')

const program2 = pipe(
  read,
  chain(() => modify),
  chain(() => read)
)

We can even define a combinator and leverage it to make the code more compact:

const interleave = <A, B>(action: IO<A>, middle: IO<B>): IO<A> =>
  pipe(
    action,
    chain(() => middle),
    chain(() => action)
  )

const program3 = interleave(read, modify)

Another example: implementing a function similar to Unix' time (the part related to the execution time) for IO.

import * as IO from 'fp-ts/IO'
import { now } from 'fp-ts/Date'
import { log } from 'fp-ts/Console'
import { pipe } from 'fp-ts/function'

// logs the computation lenght in milliseconds
export const time = <A>(ma: IO.IO<A>): IO.IO<A> =>
  pipe(
    now,
    IO.chain((startMillis) =>
      pipe(
        ma,
        IO.chain((a) =>
          pipe(
            now,
            IO.chain((endMillis) =>
              pipe(
                log(`Elapsed: ${endMillis - startMillis}`),
                IO.map(() => a)
              )
            )
          )
        )
      )
    )
  )

Digression. As you can notice, using chain when it is required to maintain a scope leads to verbose code. In languages that support monadic style natively there is often syntax support that goes by the name of "do notation" which eases this kind of situations.

Let's see a Haskell example

now :: IO Int
now = undefined -- `undefined` in Haskell is equivalent to TypeScript's declare

log :: String -> IO ()
log = undefined

time :: IO a -> IO a
time ma = do
  startMillis <- now
  a <- ma
  endMillis <- now
  log ("Elapsed:" ++ show (endMillis - startMillis))
  return a

TypeScript does not support such syntax, but it can be emulated with something similar:

import { log } from 'fp-ts/Console'
import { now } from 'fp-ts/Date'
import { pipe } from 'fp-ts/function'
import * as IO from 'fp-ts/IO'

// logs the computation lenght in milliseconds
export const time = <A>(ma: IO.IO<A>): IO.IO<A> =>
  pipe(
    IO.Do,
    IO.bind('startMillis', () => now),
    IO.bind('a', () => ma),
    IO.bind('endMillis', () => now),
    IO.chainFirst(({ endMillis, startMillis }) =>
      log(`Elapsed: ${endMillis - startMillis}`)
    ),
    IO.map(({ a }) => a)
  )

Let's see a usage example of the time combinator:

import { randomInt } from 'fp-ts/Random'
import { Monoid, concatAll } from 'fp-ts/Monoid'
import { replicate } from 'fp-ts/ReadonlyArray'

const fib = (n: number): number => (n <= 1 ? 1 : fib(n - 1) + fib(n - 2))

// launches `fib` with a random integer between 30 and 35
// logging both the input and output
const randomFib: IO.IO<void> = pipe(
  randomInt(30, 35),
  IO.chain((n) => log([n, fib(n)]))
)

// a monoid instance for `IO<void>`
const MonoidIO: Monoid<IO.IO<void>> = {
  concat: (first, second) => () => {
    first()
    second()
  },
  empty: IO.of(undefined)
}

// executes `n` times the `mv` computation
const replicateIO = (n: number, mv: IO.IO<void>): IO.IO<void> =>
  concatAll(MonoidIO)(replicate(n, mv))

// -------------------
// usage example
// -------------------

time(replicateIO(3, randomFib))()
/*
[ 31, 2178309 ]
[ 33, 5702887 ]
[ 30, 1346269 ]
Elapsed: 89
*/

Logs also the partial:

time(replicateIO(3, time(randomFib)))()
/*
[ 33, 5702887 ]
Elapsed: 54
[ 30, 1346269 ]
Elapsed: 13
[ 32, 3524578 ]
Elapsed: 39
Elapsed: 106
*/

One of the most interesting aspects of working with the monadic interface (map, of, chain) is the possibility to inject dependencies which the program needs, including the way of concatenating different computations.

To see that, let's refactor the small program that reads and writes a file:

import { IO } from 'fp-ts/IO'
import { pipe } from 'fp-ts/function'

// -----------------------------------------
// Deps interface, what we would call a "port" in the Hexagonal Architecture
// -----------------------------------------

interface Deps {
  readonly readFile: (filename: string) => IO<string>
  readonly writeFile: (filename: string, data: string) => IO<void>
  readonly log: <A>(a: A) => IO<void>
  readonly chain: <A, B>(f: (a: A) => IO<B>) => (ma: IO<A>) => IO<B>
}

// -----------------------------------------
// program
// -----------------------------------------

const program4 = (D: Deps) => {
  const modifyFile = (filename: string, f: (s: string) => string) =>
    pipe(
      D.readFile(filename),
      D.chain((s) => D.writeFile(filename, f(s)))
    )

  return pipe(
    D.readFile('file.txt'),
    D.chain(D.log),
    D.chain(() => modifyFile('file.txt', (s) => s + '\n// eof')),
    D.chain(() => D.readFile('file.txt')),
    D.chain(D.log)
  )
}

// -----------------------------------------
// a `Deps` instance, what we would call an "adapter" in the Hexagonal Architecture
// -----------------------------------------

import * as fs from 'fs'
import { log } from 'fp-ts/Console'
import { chain } from 'fp-ts/IO'

const DepsSync: Deps = {
  readFile: (filename) => () => fs.readFileSync(filename, 'utf-8'),
  writeFile: (filename: string, data: string) => () =>
    fs.writeFileSync(filename, data, { encoding: 'utf-8' }),
  log,
  chain
}

// dependency injection
program4(DepsSync)()

There's more, we can even abstract the effect in which the program runs. We can define our own FileSystem effect (the effect representing read-write operations over the file system):

import { IO } from 'fp-ts/IO'
import { pipe } from 'fp-ts/function'

// -----------------------------------------
// our program's effect
// -----------------------------------------

interface FileSystem<A> extends IO<A> {}

// -----------------------------------------
// dependencies
// -----------------------------------------

interface Deps {
  readonly readFile: (filename: string) => FileSystem<string>
  readonly writeFile: (filename: string, data: string) => FileSystem<void>
  readonly log: <A>(a: A) => FileSystem<void>
  readonly chain: <A, B>(
    f: (a: A) => FileSystem<B>
  ) => (ma: FileSystem<A>) => FileSystem<B>
}

// -----------------------------------------
// program
// -----------------------------------------

const program4 = (D: Deps) => {
  const modifyFile = (filename: string, f: (s: string) => string) =>
    pipe(
      D.readFile(filename),
      D.chain((s) => D.writeFile(filename, f(s)))
    )

  return pipe(
    D.readFile('file.txt'),
    D.chain(D.log),
    D.chain(() => modifyFile('file.txt', (s) => s + '\n// eof')),
    D.chain(() => D.readFile('file.txt')),
    D.chain(D.log)
  )
}

With a simple change in the definition of the FileSystem effect. we can modify the program to make it run asynchronously

// -----------------------------------------
// our program's effect
// -----------------------------------------

-interface FileSystem<A> extends IO<A> {}
+interface FileSystem<A> extends Task<A> {}

now all there's left is to modify the Deps instance to adapt to the new definition.

import { Task } from 'fp-ts/Task'
import { pipe } from 'fp-ts/function'

// -----------------------------------------
// our program's effect (modified)
// -----------------------------------------

interface FileSystem<A> extends Task<A> {}

// -----------------------------------------
// dependencies (NOT modified)
// -----------------------------------------

interface Deps {
  readonly readFile: (filename: string) => FileSystem<string>
  readonly writeFile: (filename: string, data: string) => FileSystem<void>
  readonly log: <A>(a: A) => FileSystem<void>
  readonly chain: <A, B>(
    f: (a: A) => FileSystem<B>
  ) => (ma: FileSystem<A>) => FileSystem<B>
}

// -----------------------------------------
// program (NOT modified)
// -----------------------------------------

const program5 = (D: Deps) => {
  const modifyFile = (filename: string, f: (s: string) => string) =>
    pipe(
      D.readFile(filename),
      D.chain((s) => D.writeFile(filename, f(s)))
    )

  return pipe(
    D.readFile('file.txt'),
    D.chain(D.log),
    D.chain(() => modifyFile('file.txt', (s) => s + '\n// eof')),
    D.chain(() => D.readFile('file.txt')),
    D.chain(D.log)
  )
}

// -----------------------------------------
// a `Deps` instance (modified)
// -----------------------------------------

import * as fs from 'fs'
import { log } from 'fp-ts/Console'
import { chain, fromIO } from 'fp-ts/Task'

const DepsAsync: Deps = {
  readFile: (filename) => () =>
    new Promise((resolve) =>
      fs.readFile(filename, { encoding: 'utf-8' }, (_, s) => resolve(s))
    ),
  writeFile: (filename: string, data: string) => () =>
    new Promise((resolve) => fs.writeFile(filename, data, () => resolve())),
  log: (a) => fromIO(log(a)),
  chain
}

// dependency injection
program5(DepsAsync)()

Quiz. The previous examples overlook, on purpose, possible errors. Example give: the file we're operating on may not exist at all. How could we modify the FileSystem effect to take this into account?

import { Task } from 'fp-ts/Task'
import { pipe } from 'fp-ts/function'
import * as E from 'fp-ts/Either'

// -----------------------------------------
// our program's effect (modified)
// -----------------------------------------

interface FileSystem<A> extends Task<E.Either<Error, A>> {}

// -----------------------------------------
// dependencies (NOT modified)
// -----------------------------------------

interface Deps {
  readonly readFile: (filename: string) => FileSystem<string>
  readonly writeFile: (filename: string, data: string) => FileSystem<void>
  readonly log: <A>(a: A) => FileSystem<void>
  readonly chain: <A, B>(
    f: (a: A) => FileSystem<B>
  ) => (ma: FileSystem<A>) => FileSystem<B>
}

// -----------------------------------------
// program (NOT modified)
// -----------------------------------------

const program5 = (D: Deps) => {
  const modifyFile = (filename: string, f: (s: string) => string) =>
    pipe(
      D.readFile(filename),
      D.chain((s) => D.writeFile(filename, f(s)))
    )

  return pipe(
    D.readFile('-.txt'),
    D.chain(D.log),
    D.chain(() => modifyFile('file.txt', (s) => s + '\n// eof')),
    D.chain(() => D.readFile('file.txt')),
    D.chain(D.log)
  )
}

// -----------------------------------------
// `Deps` instance (modified)
// -----------------------------------------

import * as fs from 'fs'
import { log } from 'fp-ts/Console'
import { chain, fromIO } from 'fp-ts/TaskEither'

const DepsAsync: Deps = {
  readFile: (filename) => () =>
    new Promise((resolve) =>
      fs.readFile(filename, { encoding: 'utf-8' }, (err, s) => {
        if (err !== null) {
          resolve(E.left(err))
        } else {
          resolve(E.right(s))
        }
      })
    ),
  writeFile: (filename: string, data: string) => () =>
    new Promise((resolve) =>
      fs.writeFile(filename, data, (err) => {
        if (err !== null) {
          resolve(E.left(err))
        } else {
          resolve(E.right(undefined))
        }
      })
    ),
  log: (a) => fromIO(log(a)),
  chain
}

// dependency injection
program5(DepsAsync)().then(console.log)

데모

06_game.ts