Bayesian AB Test Report Builder

Baker Moran

This is a package to allow AB testers to create a standard report for test results. Can handle conversion and continuous data. Can handle multiple variants.

Conversion data uses the beta distribution as the conjugate prior, and continuous data uses the log-normal.

Instantiation variables

• raw_data - a pandas dataframe with (at least) two columns, one for the bucket and one for the response variable
• metric - column name in raw_data for the response variable
• bucket_col_name - column name in raw_data for the bucket (defaults to bucket)
• control_bucket_name - value in bucket_col_name for the control bucket (defaults to off)
• samples - number of samples to run the monte carlo simulation, must be 1,000 and 50,000 (defaults to 10,000)
• prior_func - the type of distribution to use for the prior. options include:
  • beta - use for conversion rates. bounded on the interval [0,1]
  • log-normal - use for continuous, greater than zero response variables (0, +inf) (ex: premium, minutes spent on scene, etc.)
  • normal - use for continuous response variables that on the interval (-inf, +inf)
  • poisson - use for discrete, greater than zero response variables (ex: arrivals per day, events per account, etc.)
• prior_info - the prior belief to about the response varable. options include:
  • uninformed - no prior belief about the response, all outcomes are equaly likely. No input required to use
  • informed - uses and empirically informed prior (informed by the control data), and weakens this prior by prior_scale_factor
  • specified - allows for a user to input prior parameters
• prior_parameters - prior_info must be set to specified. This must be a dictionary with the following key value pairs:
  • prior_func = beta - keys are alpha and beta
  • prior_func = log-normal - keys are mean and var
  • prior_func = normal - keys are mean and var
  • prior_func = poisson - keys are alpha and beta OR mean and var
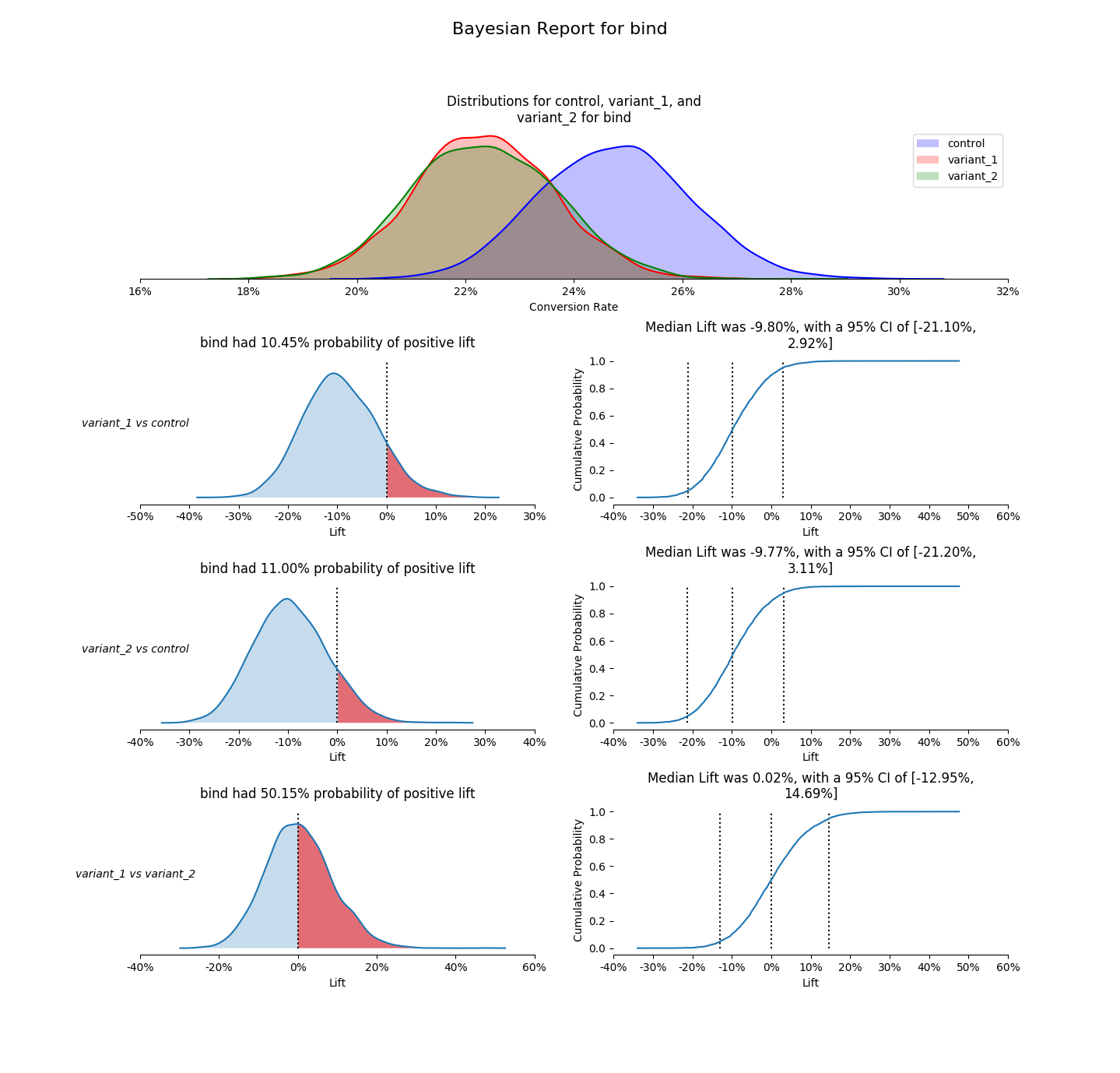
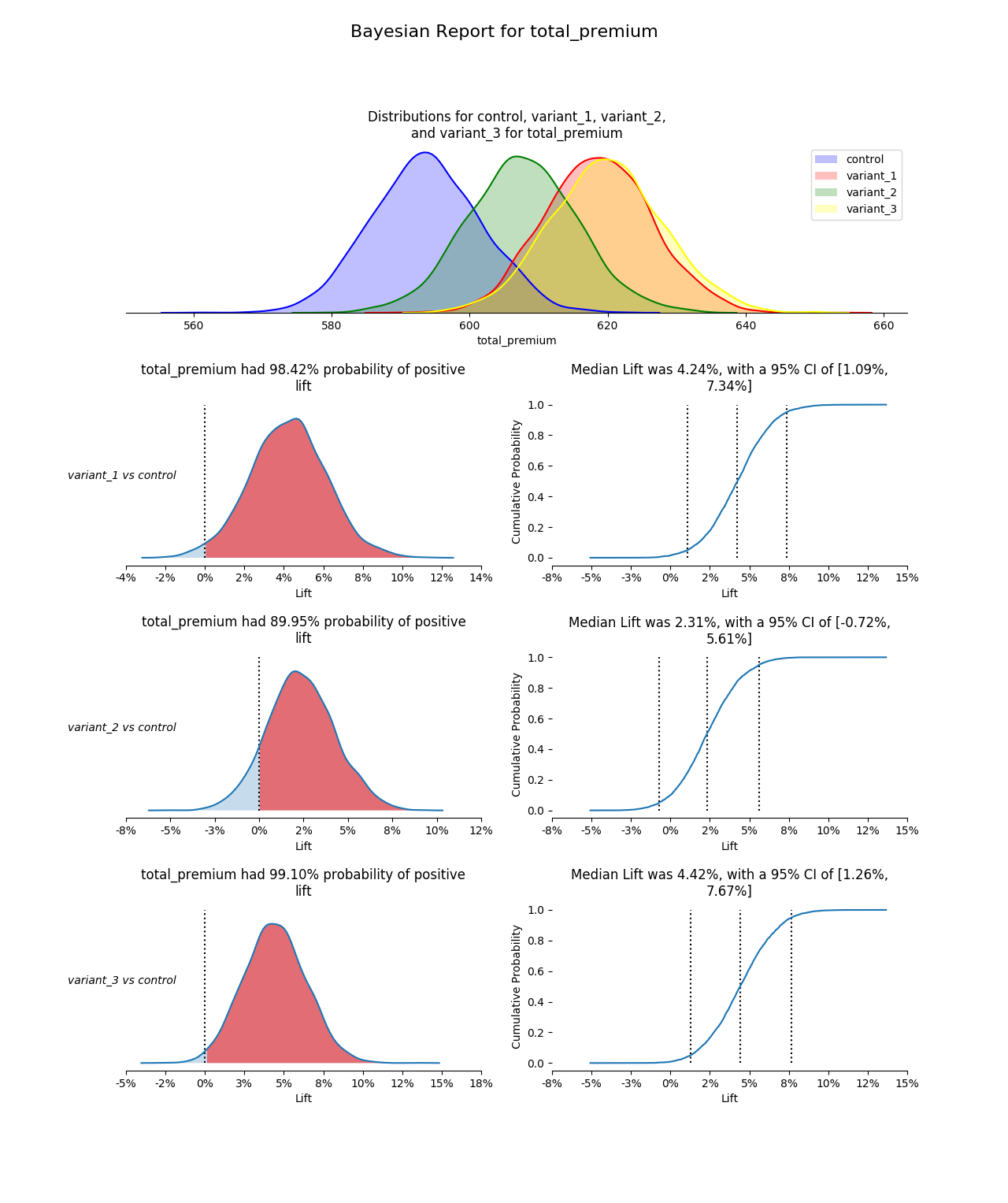
• confidence_level - value for the confidence interval on the CDF chart (defaults to 0.05)
• compare_variants - boolean for comparing the variants to each other. Control to each variant is always done (unless there are too many variants to plot). If there are few enough variants, the comparisons for variants will be plotted. (defaults to False)
• debug - boolean to print out extra output for debugging purposes (defaults to False)
• prior_scale_factor - factor to scale an empirically informed prior by (defaults to 4)

Public class methods and variables

Methods

• fit()
  • requires - class was instantiated with valid inputs
  • modifies - ecdf, control_sample, variant_sample, lift
  • effects - creates and runs the monte carlo simulation, sets member variables to reflect model outputs
• plot(lift_plot_flag=True)
  • lift_plot_flag - boolean for plotting lift PDF and CDF (defaults to True)
  • requires - fit() has been run
  • modifies - none
  • effects - creates a 3 chart report of the AB test. (must show with matplotlib.pylot.show())
• plot_posteriors(variants=[]):
  • requires - variants is a list of variant names in bucket_col_name. One variant may not be repeated multiple times.
  • modifies - none
  • effects - creates a posterior plot of these variants (must show with matplotlib.pylot.show())
• plot_positive_lift(variant_one, variant_two)
  • requires - variant_one and variant_two are variant names in bucket_col_name. One variant may not be repeated multiple times.
  • modifies - none
  • effects - creates a positive lift plot between these variants (must show with matplotlib.pylot.show())
• plot_ecdf(variant_one, variant_two)
  • requires - variant_one and variant_two are variant names in bucket_col_name. One variant may not be repeated multiple times.
  • modifies - none
  • effects - creates an empirical cumulative distribution plot of these variants lift (must show with matplotlib.pylot.show())

Variables

• all variables in Instantiation variables
• ecdf - a 3 level dicitonary, where key1 is a the variant name of the numerator in the lift calculation, and key2 is the variant name of the denominator in the lift calculation. The third keys are x and y, and the value is a list containing the x and y coordinates for the empirical CDF (only meaningful after fit() is run)
• lift - a 2 level dicitonary, where key1 is a the variant name of the numerator in the lift calculation, and key2 is the variant name of the denominator in the lift calculation. The value is a list containing the lift of the variant over the control for each sampled value (only meaningful after fit() is run)
• posteriors is a dictionary, where the key is a variant name, and the value is a posterior_distribution object.

Usage guide

First install package. Navigate to the directory in terminal and pip install it.

cd BayesABTest
pip3 install -e .

Second, import in your analysis file.

import pandas as pd
from BayesABTest import ab_test_model

# read in data
df = pd.read_csv('some_file.csv')

# initialize class with the data and some optional variables
first_test = ab_test_model(df, metric='bind', prior_info='informed', prior_func='beta', debug=True)

# run public methods
first_test.fit()
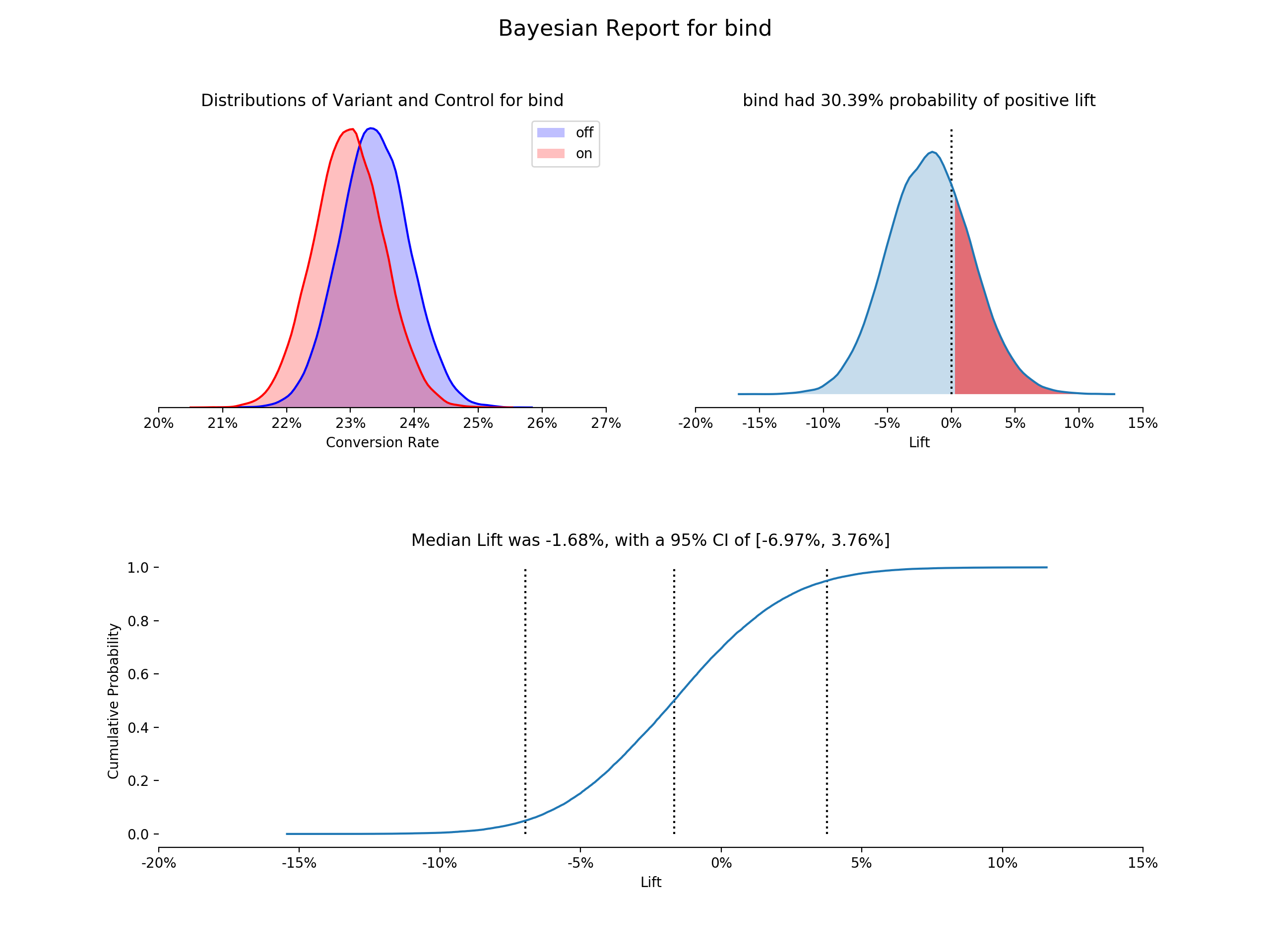
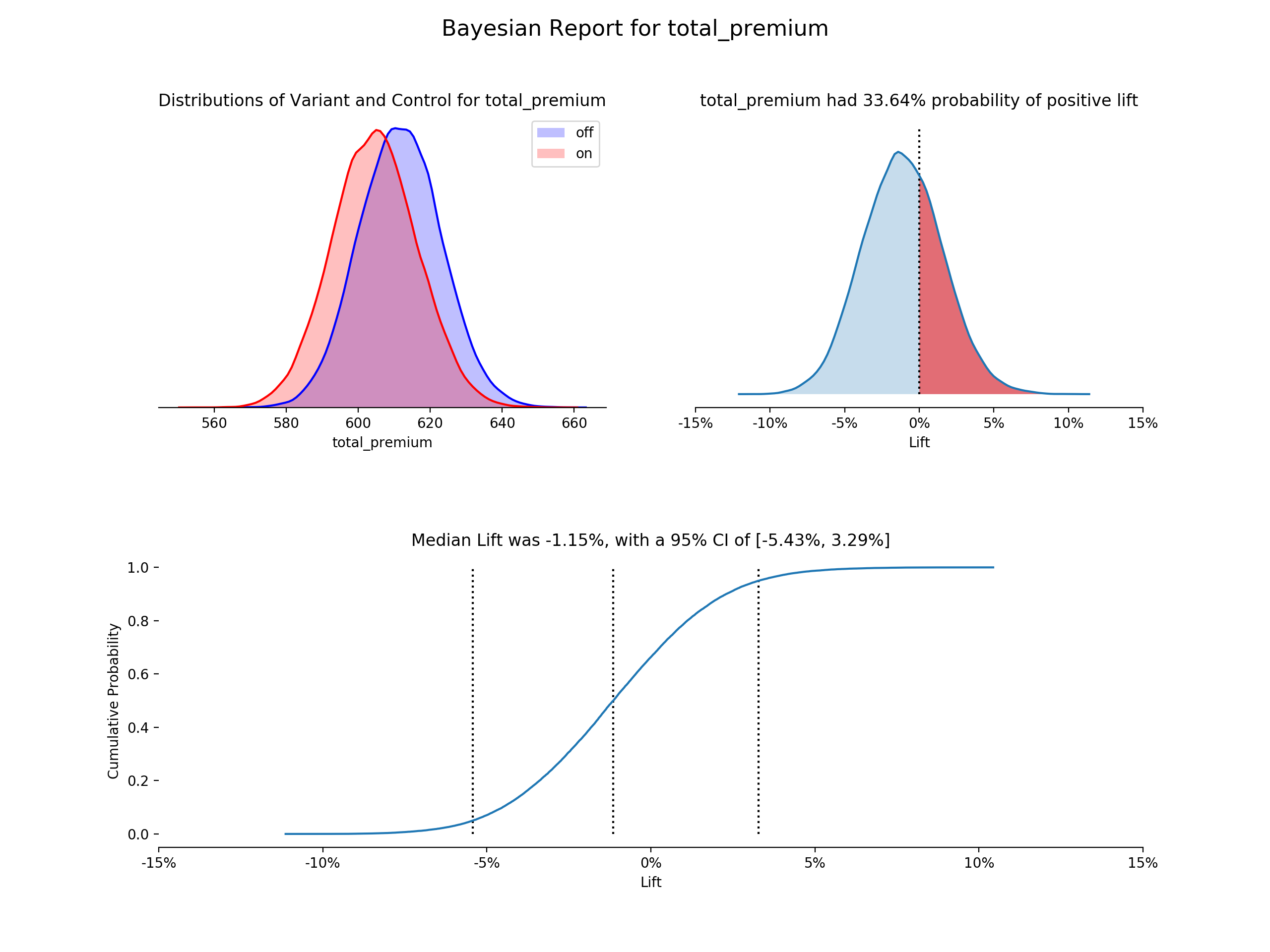
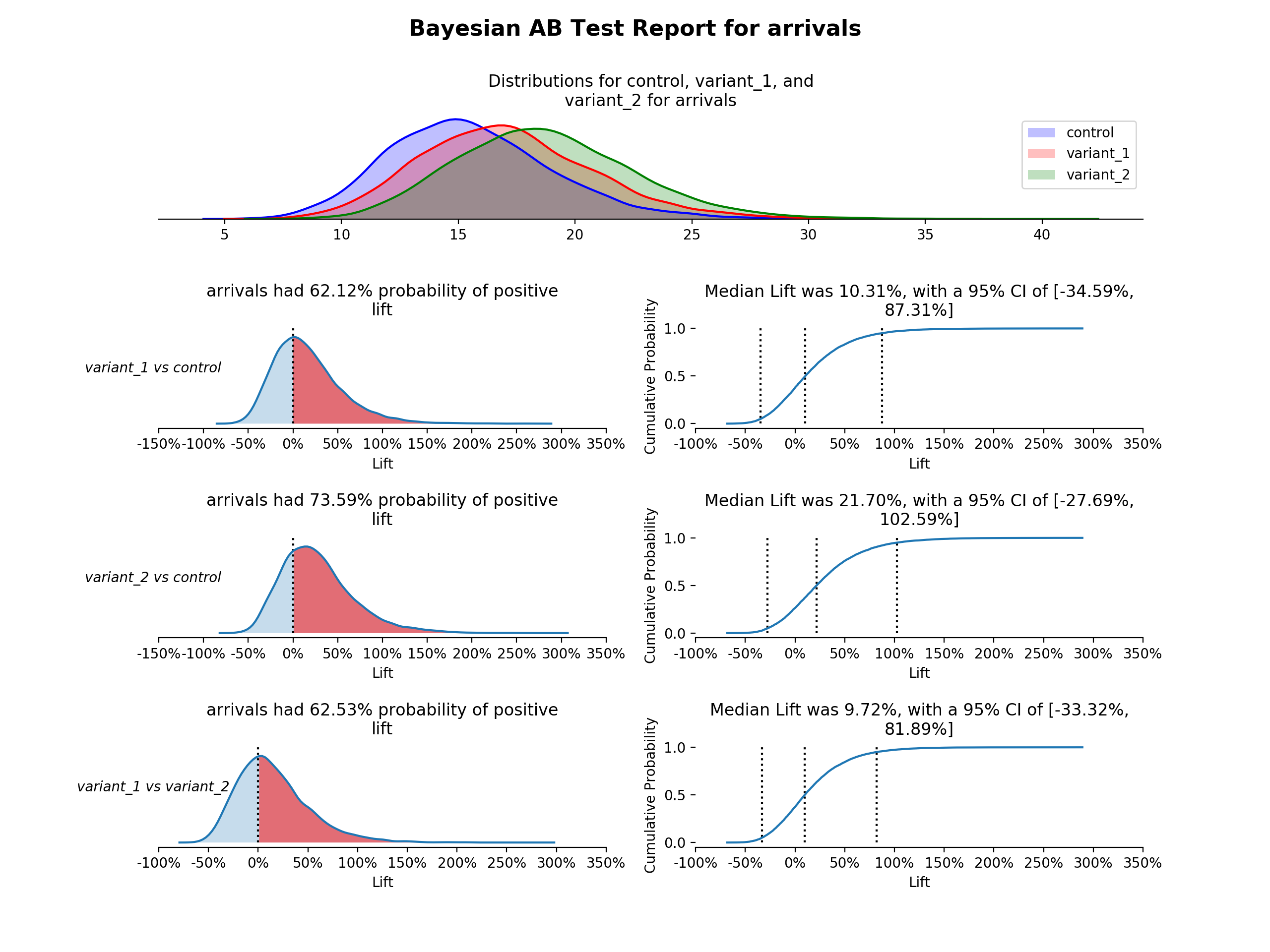
first_test.plot()

Example output

Chart Type Descriptions (Top Left -> Clockwise)

• Posterior Distributions - Shows both buckets posterior distributions, an estimate of the true conversion rate or continuous value, based on the prior and the observed data (using kernel density estimation plots)
• Lift PDF - Shows the probability density distribution of lift for the variant over the control, an estimate of the chance of improvement of the variant over the control (using kernel density estimation plot). Calculated by: the results from the sampled values for the variant percent change from the control. The proportion greater than 0 is highlighted.
• Empirical CDF of Liftå - Uses the same lift vector, but is the empirical cumulative distribution function. Median lift is highlighted and labeled, as well as the chosen confidence interval.

Conversion Rate Example (Beta Distribution)

Continuous (Positive) Variable Example (Log-Normal Distribution)

Two Variant Conversion with Compare Variants

Three Variant Continuous without Comparing Variants

Two Variant Poisson with Comparing Variants

Version History

• 0.1.0 - 12/02/2019
• 1.0.0 - 12/27/2019
• 1.0.1 - 01/02/2020
• 1.0.2 - 02/11/2020
• 1.0.3 - 02/21/2020

Acknowledgements

There is a lot of documentation out there about a Bayesian framework of A/B testing. Some of the specific articles are listed below. Most of the work I came across was written in R, and I set out to create a Python implementation. The visuals were inspired by a standard template we use at Root, first written by https://github.com/zachurchill-root.

Articles Reference:

• https://www.countbayesie.com/blog/2015/4/25/bayesian-ab-testing
• https://medium.com/convoy-tech/the-power-of-bayesian-a-b-testing-f859d2219d5
• https://cdn2.hubspot.net/hubfs/310840/VWO_SmartStats_technical_whitepaper.pdf