LCR 171. 训练计划 V.md

解题思路：

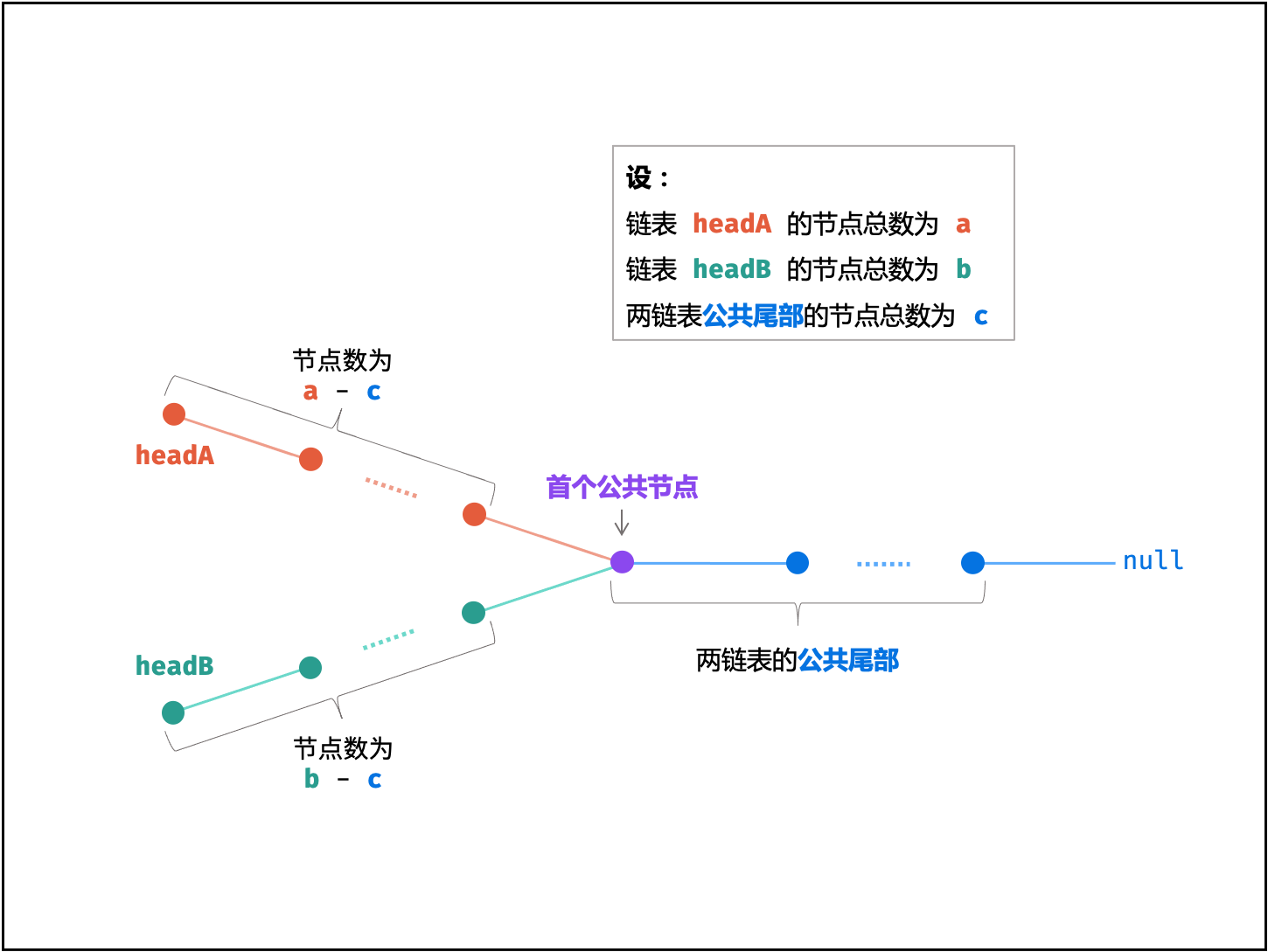
设第一个公共节点为 node ，链表 headA 的节点数量为 $a$ ，链表 headB 的节点数量为 $b$ ，两链表的公共尾部的节点数量为 $c$ ，则有：

• 头节点 headA 到 node 前，共有 $a - c$ 个节点；
• 头节点 headB 到 node 前，共有 $b - c$ 个节点；

{:align=center width=500}

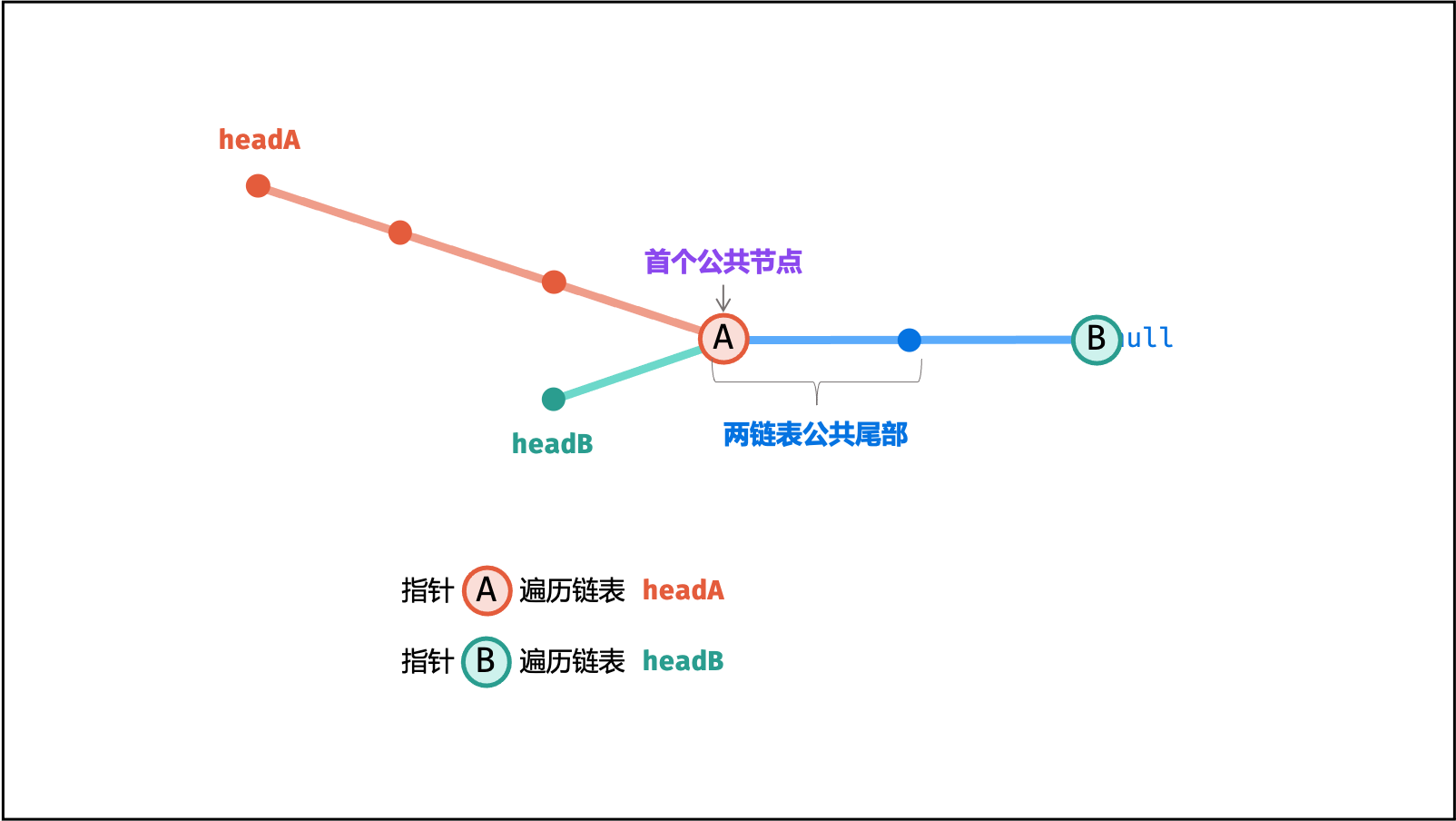
考虑构建两个节点指针 A​ , B 分别指向两链表头节点 headA , headB ，做如下操作：

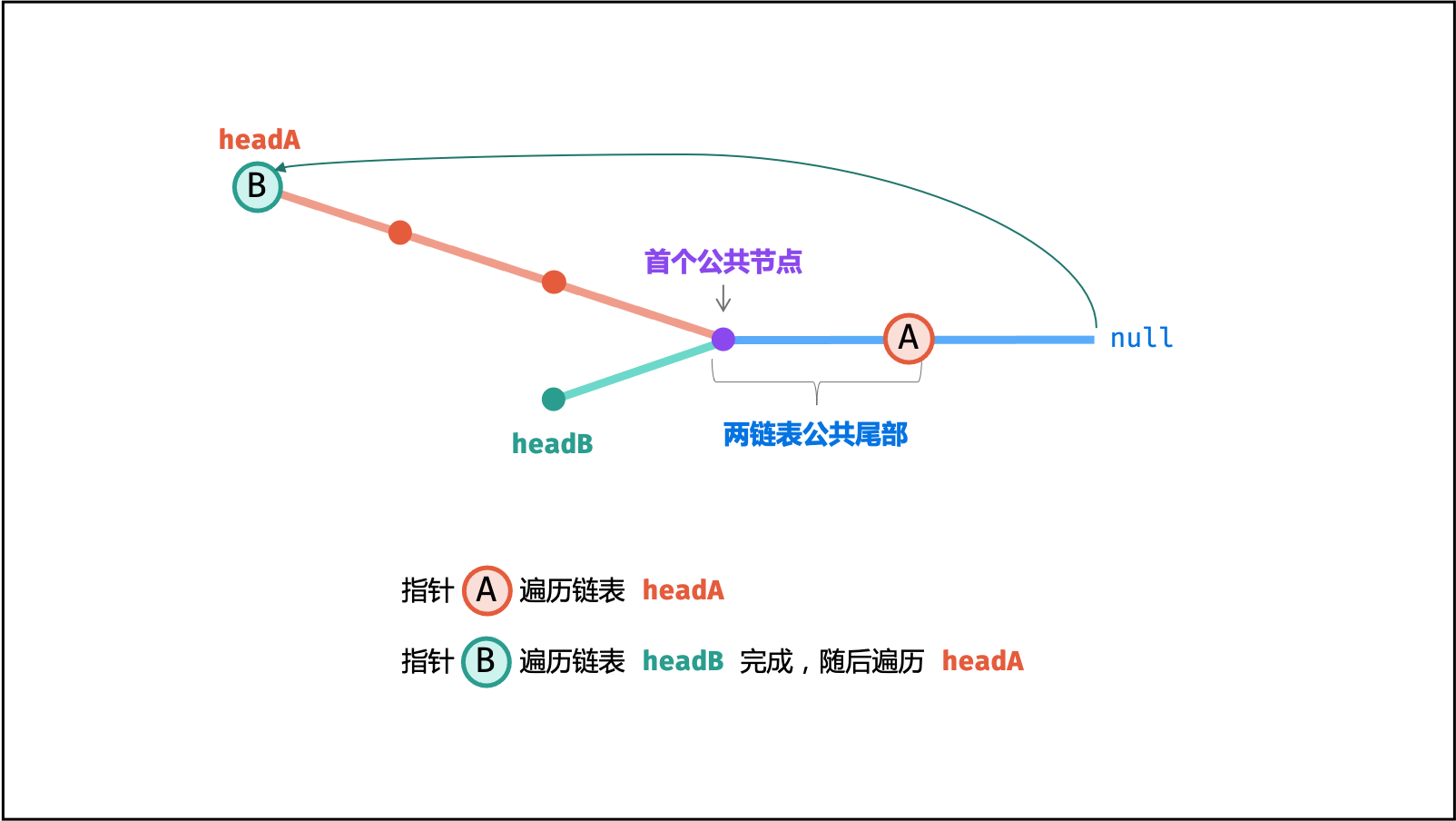
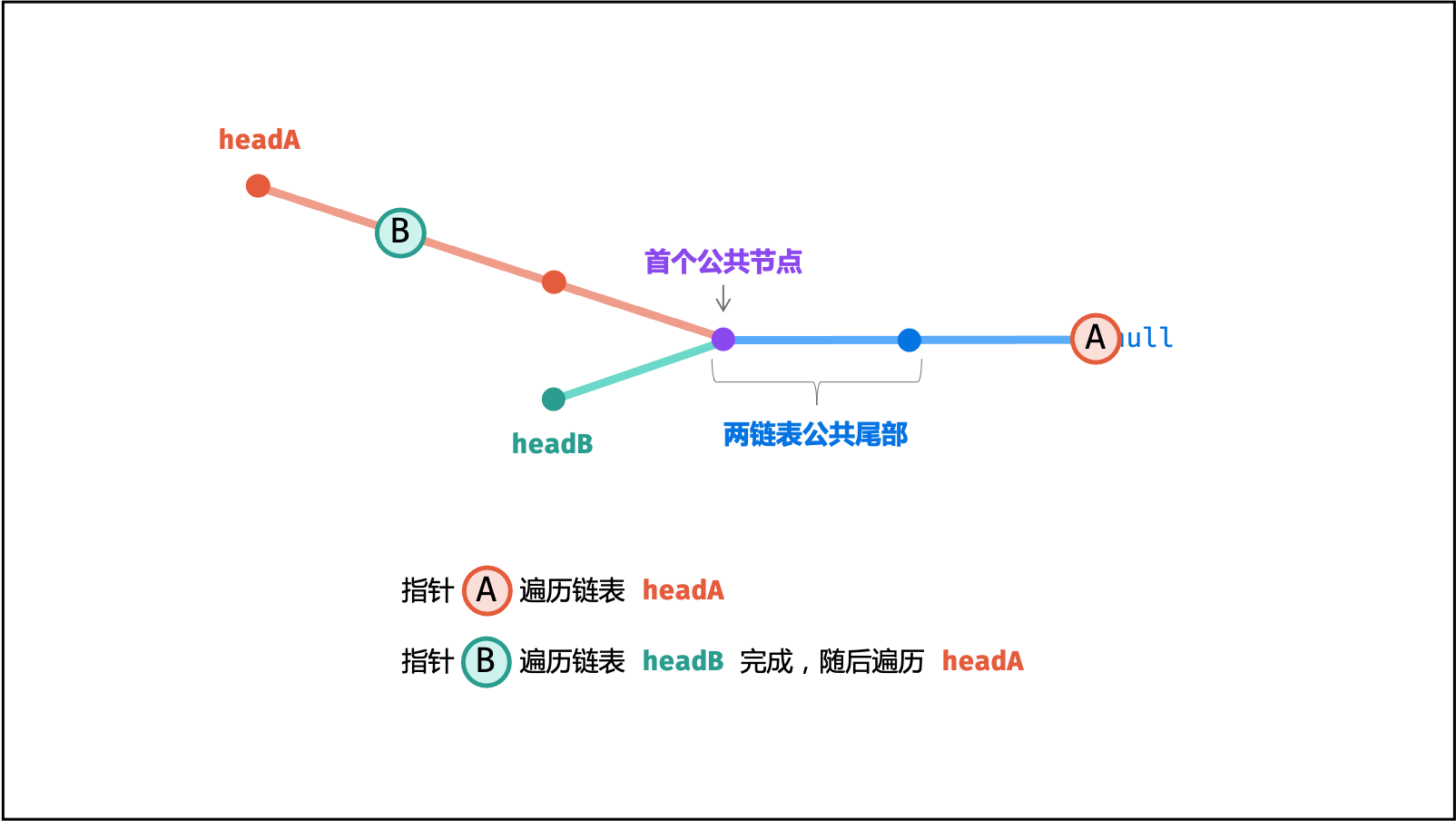
• 指针 A 先遍历完链表 headA ，再开始遍历链表 headB ，当走到 node 时，共走步数为：

$$ a + (b - c) $$

• 指针 B 先遍历完链表 headB ，再开始遍历链表 headA ，当走到 node 时，共走步数为：

$$ b + (a - c) $$

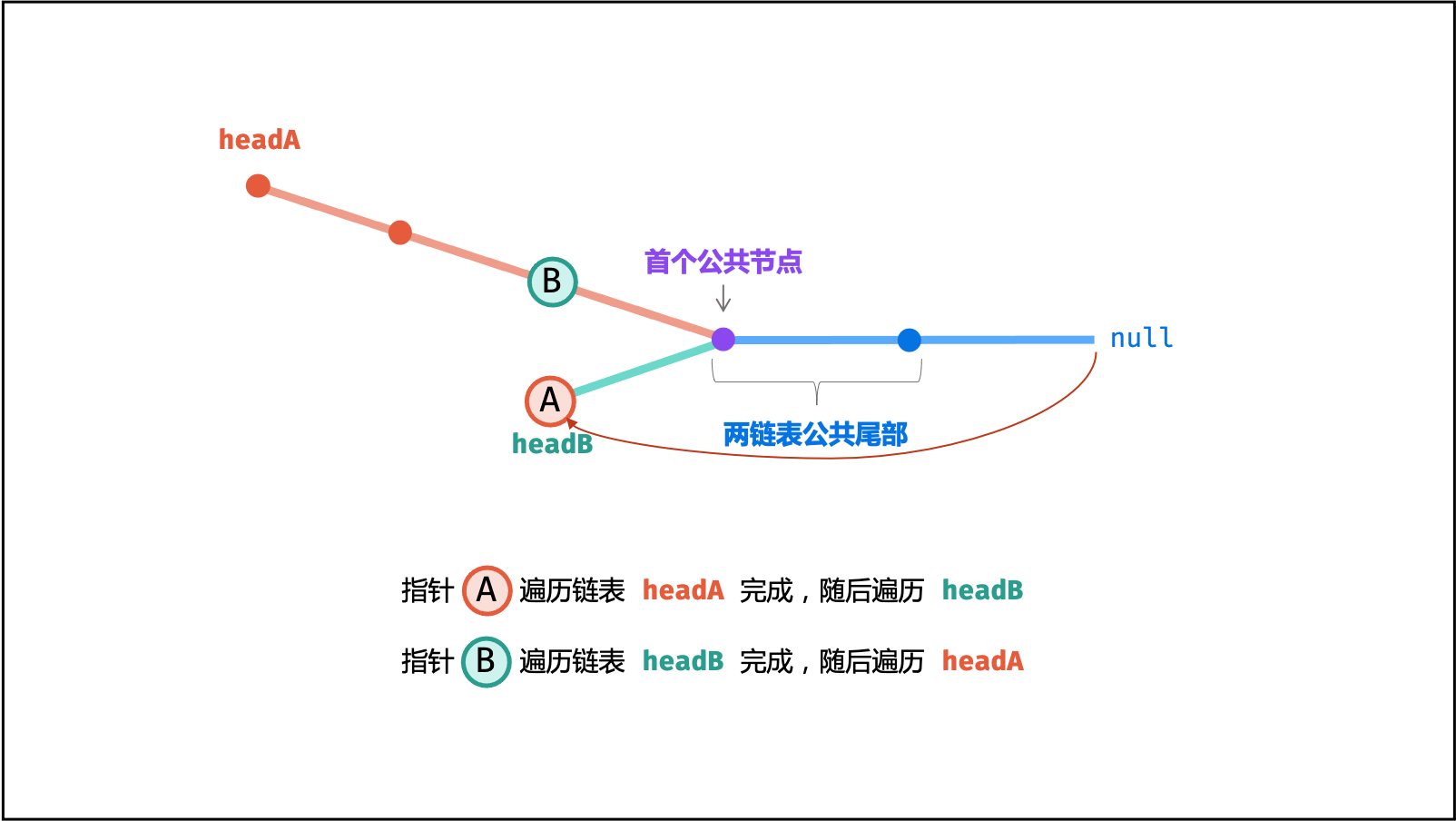
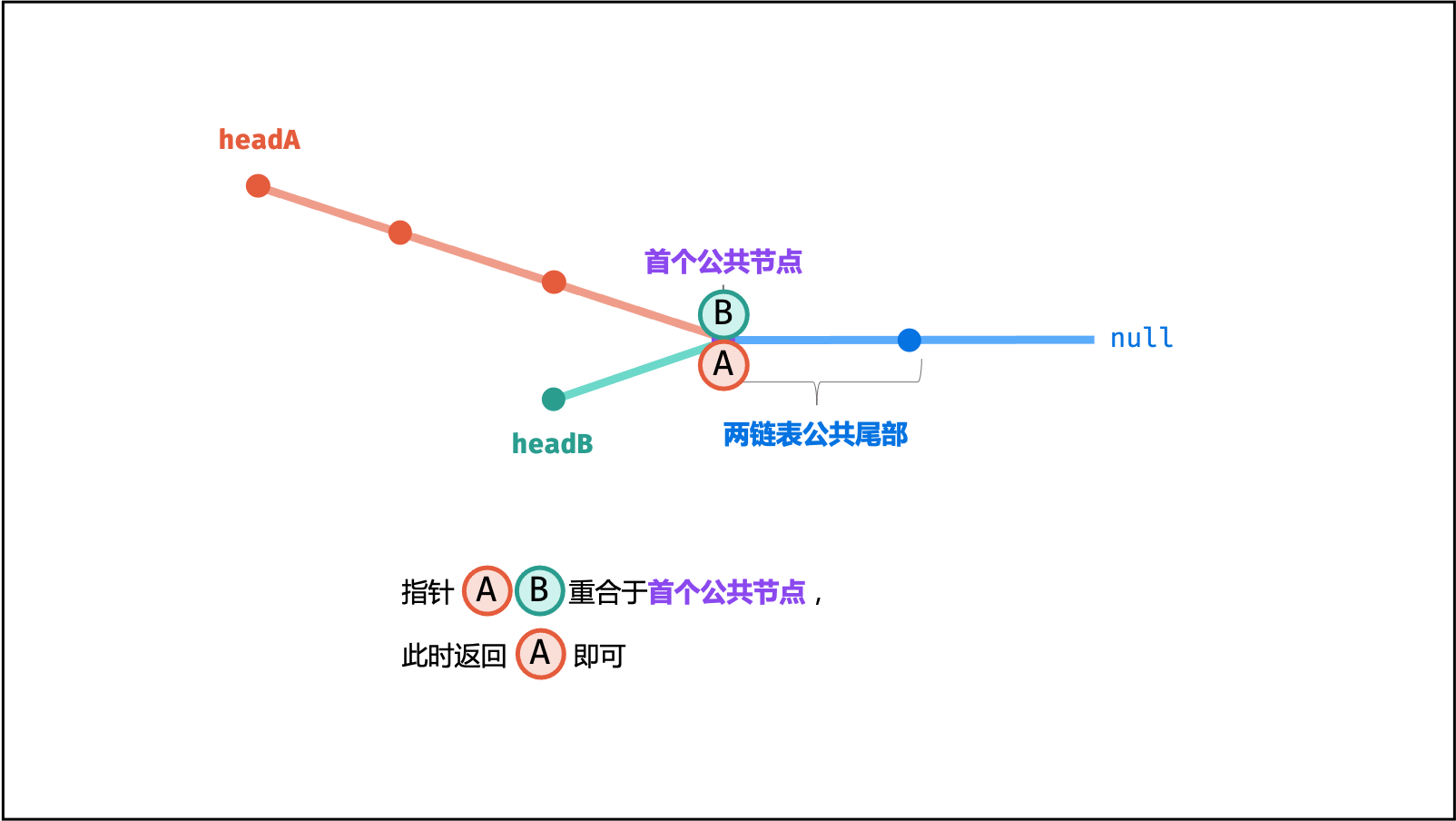
如下式所示，此时指针 A , B 重合，并有两种情况：

$$ a + (b - c) = b + (a - c) $$

1. 若两链表 有 公共尾部 (即 $c > 0$ ) ：指针 A , B 同时指向「第一个公共节点」node 。
2. 若两链表 无 公共尾部 (即 $c = 0$ ) ：指针 A , B 同时指向 $\text{null}$ 。

因此返回 A 即可。

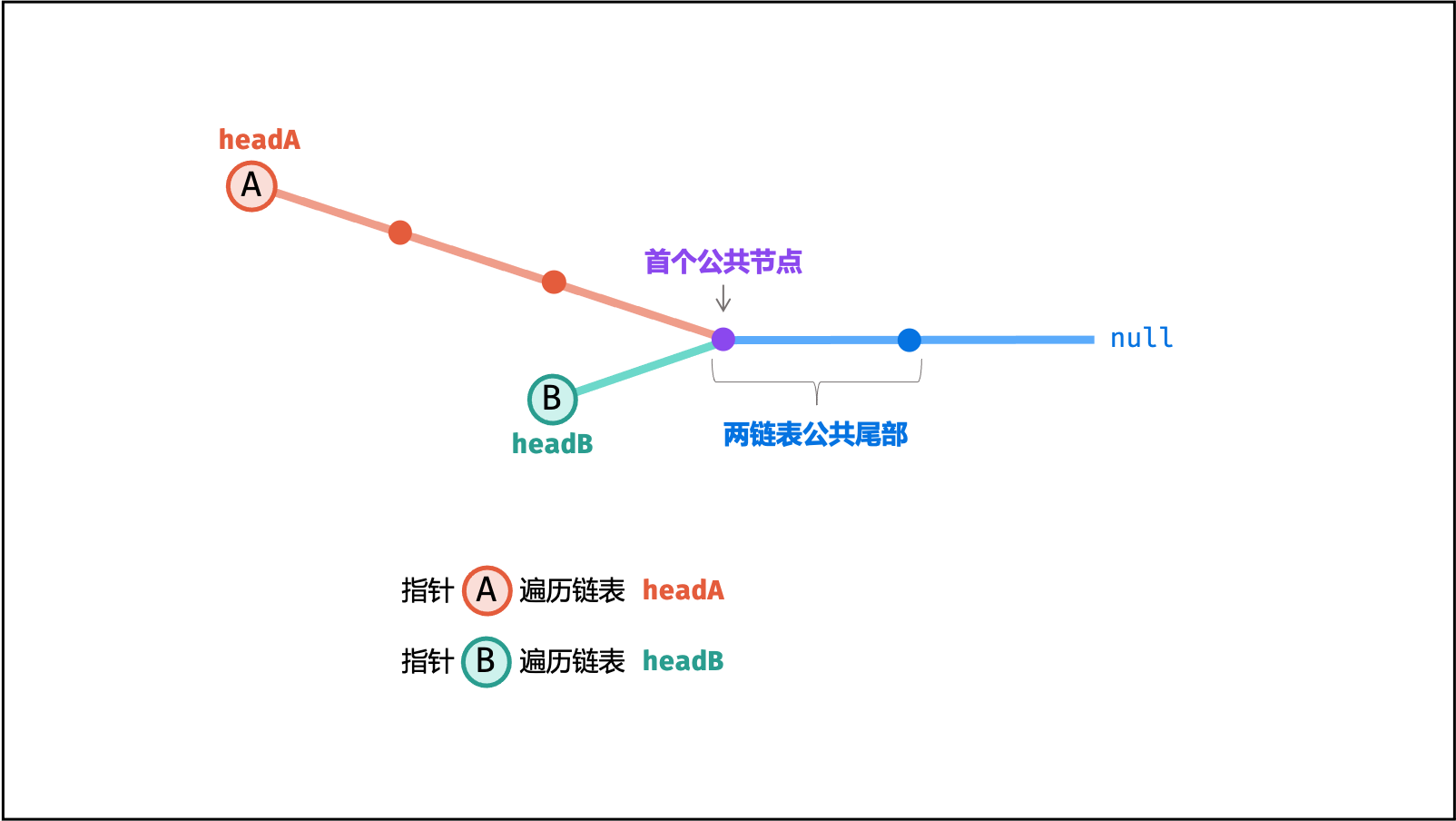
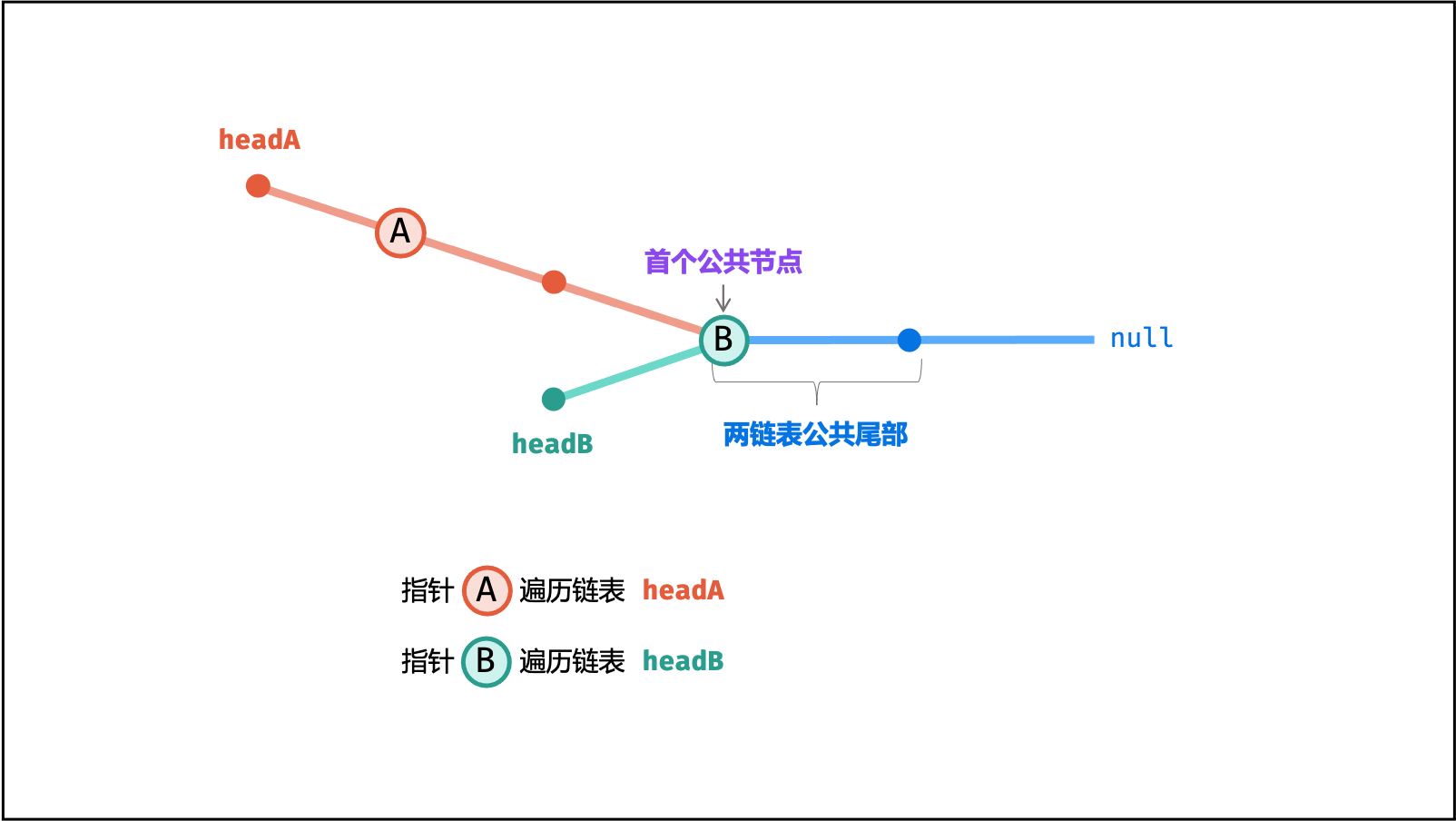
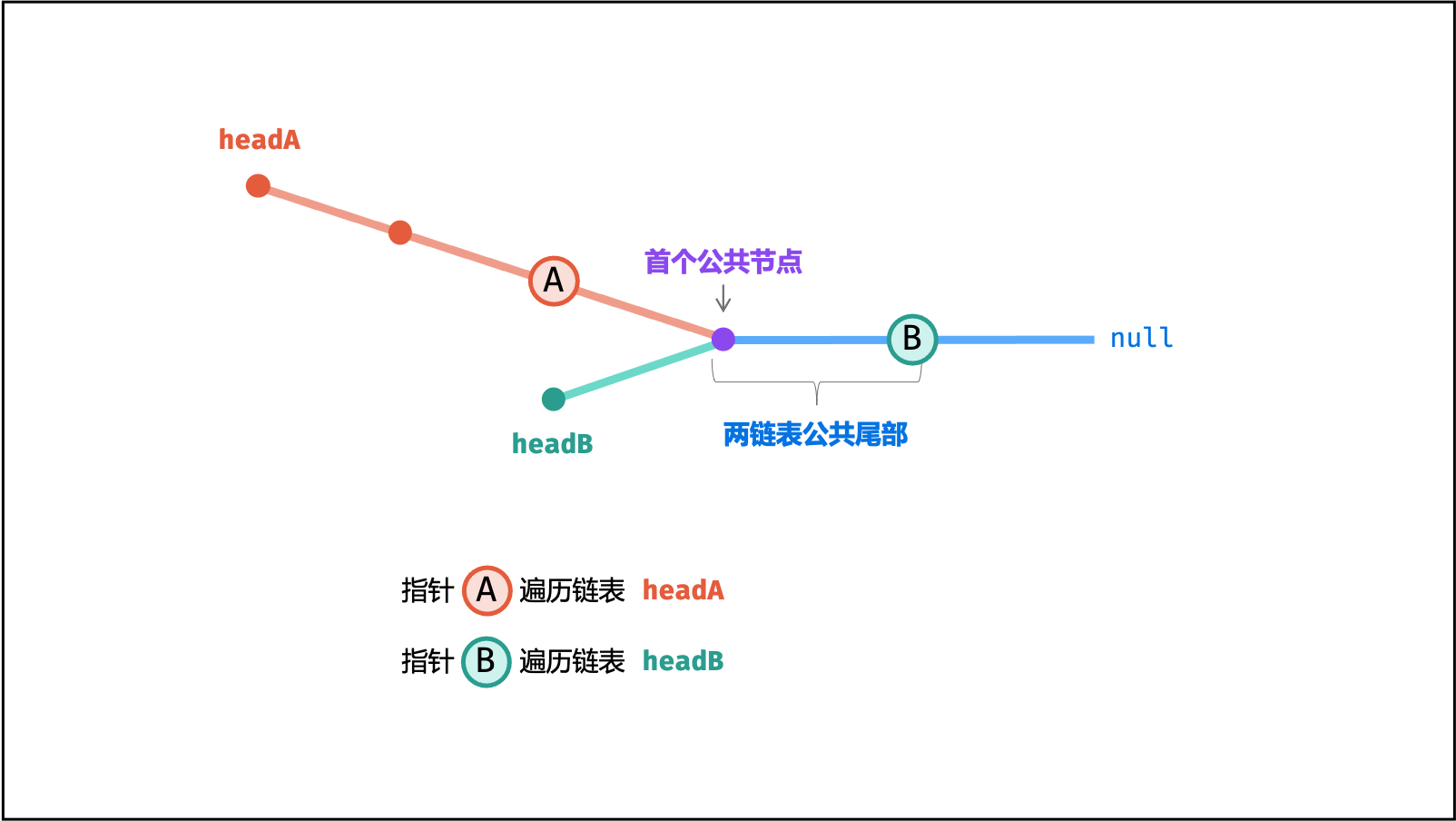
下图展示了 $a = 5$ , $b = 3$ , $c = 2$ 示例的算法执行过程。

<,,,,,,,>

代码：

class Solution:
    def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
        A, B = headA, headB
        while A != B:
            A = A.next if A else headB
            B = B.next if B else headA
        return A

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode A = headA, B = headB;
        while (A != B) {
            A = A != null ? A.next : headB;
            B = B != null ? B.next : headA;
        }
        return A;
    }
}

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode *A = headA, *B = headB;
        while (A != B) {
            A = A != nullptr ? A->next : headB;
            B = B != nullptr ? B->next : headA;
        }
        return A;
    }
};

复杂度分析：

• 时间复杂度 $O(a + b)$ ： 最差情况下（即 $|a - b| = 1$ , $c = 0$ ），此时需遍历 $a + b$ 个节点。
• 空间复杂度 $O(1)$ ： 节点指针 A , B 使用常数大小的额外空间。