DTAM里面对每个像素都进行直接法的跟踪,
而 LSD SLAM里 只对 “有纹理”(梯度大的地方) 的区域进行估计,不估计令每一个做SLAM的人都害怕的终极大魔头——“大白墙”部分
估计深度的部分在原理上也是direct method,和DTAM类似.
先从图片中提取特征点并进行匹配,然后进行优化求解,这类方法称为特征法或间接法。
由于提取、匹配的过程中耗时很大,因此有人提出是否能不计算关键点或描述子,
直接根据图像的像素信息来计算相机运动,这类方法称为直接法。
tracking optimizationThreadLoop线程 分析等
lsd:constraintSearchThreadLoop线程
平移,旋转,相似以及投影变换,在lsd-slam中, 有个三方开源库叫做Sophus/sophus,封装好了前三个变换。 库分析 Sophus/sophus
Dense+Indirect:
基本方法:光流场的平滑度 + 几何误差(光流求导)
DTAM(直接法跟踪全部像素点,稠密方法)
LSD(选取整幅图像中有梯度的部分来采用直接法,这种方法称为半稠密方法(simi-dense)),
SVO(选取关键点来采用直接法,这类方法称为稀疏方法(sparse))
Sparse+Indirect:非直接法(即特征点法)SLAM,
基本套路是:特征点+匹配+优化方法求解最小化重投影误差。
典型代表:
Mono-SLAM,PTAM(FAST角点),ORB-SLAM(ORB特征点),以及现在大部分SLAM
按照 2D−2D 数据关联方式的不同 ,视觉定位方法可以分为直接法、非直接法和混合法
1. 直接法假设帧间光度值具有不变性 , 即相机运动前后特征点的灰度值是相同的 .
数据关联时 , 根据灰度值对特征点进行匹配,通过最小化光度误差,来优化匹配.
直接法使用了简单的成像模型 ,
适用于帧间运动较小的情形 , 但在场景的照明发生变化时容易失败 .
2. 非直接法 , 又称为特征法 , 该方法提取图像中的特征进行匹配 ,
最小化重投影误差得到位姿 . 图像中的特征点以及对应描述子用于数据关联 ,
通过特征描述子的匹配 ,完成初始化中 2D−2D 以及之后的 3D−2D 的数据关联 .
例如 ORB (Oriented FAST and rotatedBRIEF, ORBSLAM中 ) 、
FAST (Features from accelerated seg-ment test) 、
BRISK (Binary robust invariant scalable keypoints) 、
SURF (Speeded up robustfeatures) ,
或者直接的灰度块(PTAM中, 使用fast角点+灰度快匹配)
可用于完成帧间点匹配。
3. 混合法,又称为半直接法,结合直接法和特征点法
使用特征点法中的特征点提取部分,而特征点匹配不使用 特征描述子进行匹配,
而使用直接法进行匹配,利用最小化光度误差,来优化特征点的匹配,
直接法中是直接对普通的像素点(DTAM),或者灰度梯度大的点(lsd-slam)进行直接法匹配。
间接法与直接法的区别:
除了提取和匹配耗时,在使用特征点时,也忽略了除特征点以外的所有信息,因此丢弃了很多可能有用的图像信息.
间接法通过最小化几何误差geometric error)(因为预先得到的点或光流向量都是几何度量,
常用的有重投影误差(projection error)等)来进行优化从而得到相机运动;
直接法通过最小化测量误差(photometirc error,即像素之间的误差).
直接法的好处:
直接法让单独一个点不具备识别意义,而是将大量的点组织起来,因此它的表达是一种细粒度的几何表示。
直接法原理:
目标函数对变量的一阶导数,颜可比矩阵:
当前图像与当前关键帧匹配,获取姿态变换,R t:
a) SE3跟踪,参考帧根据逆深度信息,建立3d点,按照初始变换矩阵变换到当前帧坐标系下;
b) 再根据相机内参数投影到当前帧像素坐标系下;
c) 因为的得到的是浮点数类型,需要计算变换点的亚像素灰度梯度值
d) 计算参考帧像素点灰度值仿射变换值 与 当前帧变换点亚像素灰度值的误差
e) 计算加权方差归一化的误差,以及误差对应的可信度权值
f) 误差函数对变量求偏导数得到雅克比矩阵,使用迭代边权重LM优化算法,计算线性方程参数: A * dse3 = b
g) 使用 LDLT分解求取线性方程组的解 dse3
h)使用 dse3的指数映射后 对 初始位姿SE3进行更新
a. 根据极线匹配结果和运动矩阵求得深度(求极线+线匹配搜索+立体视觉三角测量得到深度);
b. 创建新的关键帧/优化当前关键帧,更新关键帧数据库;
c. 创建新的关键帧:
传播深度信息到新的关键帧,正则化深度图;
d. 优化当前关键帧:
近似为小基线长度双目,使用对极几何来估计 深度均值;
几何误差和光度误差 估计 深度方差;
概率卡尔曼滤波优化更新(扩散卡尔曼滤波),
正则化深度图;
关键帧加入当地图,从地图中匹配最相似的关键帧,估计sim3位姿变换,LM优化最小化变换误差.
G2O图优化
================================================
论文采用了最小化归一化方差的光度误差(variance-normalized photometric error):
根据匹配关系 优化变换矩阵 以及更新深度
1. 上述第一项是关于两帧之间变换矩阵的 误差函数 E(),
p为参考帧i上的关键点(最大梯度值大于阈值可以成为候选),
这里的p是在参考帧Ii观测到的有深度信息(p∈ΩDi)的归一化图像点
Di为帧i上对应的逆深度,函数 Di(p) 是点p在参考帧下的逆深度;
Vi(p) 是对应逆深度 Di(p) 的方差;
ξji 为两帧变换关系两,帧间的SE3变换(从i→j,也就是参考帧到当前帧的变换),
这里是用李代数的形式表示;
这里的σ2I是图像的高斯噪声,
sigma为误差的不确定度,作为分母,理解为加权系数,误差归一化;
函数ω(p,Di(p),ξji) 是3D投影变换(3D projective warp),把参考帧下p对应的3D点投影到当前帧的图像平面;
2. rp(p,fi) 表示 图像像素误差 Ii(p) - Ii(p') p' = w(p,D,ξji)为变换后的对应点坐标
3. sigma 与误差对逆深度导数 以及逆深度方差有关
4. ||r^2||det 误差计算分段函数方法,误差较小时 和较大时 不同的计算的fangfa
论文中在估计两帧间位姿变换的时候,把所有有逆深度假设的像素都用上了。
但是每个逆深度的确定性不同,也就是有些逆深度比较准确,有些不准确。
而准确与否则体现在逆深度的方差上了。
因此公式1中在 残差上除以了方差做了归一化。
在论文中考虑了两个方面的方差,
一个是由逆深度估计不准确引入的, 考虑逆深度 Di(p) 和 逆深度方差 Vi(p)
另外一个是由图像高斯噪声引起的。 考虑图像高斯噪声 2σ2I 和 灰度误差 rp(p,ξji)
也即是说公式3前面的是 两个图像的图像高斯噪声,
后面的是逆深度造成的误差。
这里逆深度误差不确定性是根据下式计算得到的:
Σf=JfΣxJTf
δξ∗=argmin(E(δξ∘ξ))=argmin(∑r(δξ∘ξ)^2)
接下来对光度误差做一阶泰勒展开:
ri(δξ∘ξ)=ri(ξ) + J* δξ
代入后 对δξ求导数并且使求导后的结果为0,最后可以解出增量(如下为离散的形式):
δξ(n) = −(J转置*J)逆* J转置*r(ξ(n)) ,
(J转置*J)逆* J转置 为J的伪逆
其中 转置*J 也是 函数 的二阶导数 海塞矩阵H的 雅克比矩阵的近似表达
这里对 (J转置*J)求逆比较麻烦
上式子可写为:
(J转置*J)* δξ(n) = -J转置*r(ξ(n))
即 A * δξ(n) = b
A * x = b 的形式
J是对残差向量r=(r1, … ,rk)T求导数的结果。
需要注意的是这里的ri就是 ri(ξ),k为参与优化的点的个数。
这里的新的估计值由如下形式更新:
ξ(n+1)=δξ(n)∘ξ(n)
为了减少外点(outliers)对算法的影响,
论文中使用了迭代变权重最小二乘(interatively re-weighted least-squares)的形式,
也就是在每次计算残差的时候乘以一个权重矩阵W=W(ξ(n)),
从而代价函数变为:
E(ξ)=∑ωi(ξ)*r(ξ)^2
而,更新变量为:
δξ(n) = −(J转置*J)逆* J转置*ω*r(ξ(n))
其实在实现的时候,这里给的权重 ω 就是Huber-weight。
这里里需要说明的是,在解δξ的时候,通常不采用对Hession矩阵(J转置*J)求逆的方式来解,
而是使用LDLT分解来解,也就是在对优化模型求导之后把公式整理为Ax=b的形式,
然后调用Eigen库的ldlt函数求解:
(J转置*J)* δξ(n) = -J转置*r(ξ(n))
即 A * δξ(n) = b
A * x = b 的形式
实际问题中,当求解方程组的系数矩阵是对称矩阵时,A = A转置
正交矩阵 性质 A转置 = A逆
反对称矩阵性质 B转置 = -B
对称矩阵性质 C转置 = C
则用下面介绍的LDLT分解法可以简化程序设计并减少计算量。
A有唯一的Doolittle分解A= LU。
矩阵U的对角线元素Uii 不等于0,将矩阵U的每行依次提出,得到对角矩阵D*U
即 :
A = LDU
A = LDU = A转置= (LDU)转置 = U转置 * D转置 * L转置 = U转置 * D * L转置 = A = LDU
应为分解的唯一性,可得:
U转置 = L
U = L转置 = LT这里的T表示转置的意思
则:
A = LDU = LDL转置 = LDLT , 这里LT为L的转置矩阵
记录 u = LD
v = L转置
将A分解为上面两个矩阵 相乘 A = u * v
Ax = b就可以化为u(v*x) = uy = b
先求解 y
得到 y = v*x
再求解 x
如果相机移动了足够远,那么就重新创建一个新的关键帧,否则就跟踪当前的关键帧
* (随机采样序列 8点法求解)
* 2D 点对 求 两相机的 旋转和平移矩阵
* 空间点 P 两相机 像素点对 p1 p2 两相机 归一化平面上的点对 x1 x2 与P点对应
* 相机内参数 K 两镜头旋转平移矩阵 R t 或者 变换矩阵 T
* p1 = KP (世界坐标系) p2 = K( RP + t) = KTP
* 而 x1 = K逆* p1 x2 = K逆* p2
* 相机坐标系下 归一化平面上的点:
* x1= (px -cx)/fx
* x2= (py -cy)/fy
所以 x1 = P 得到 x2 = R * x1 + t
* t 外积 x2 = t 外积 R * x1 + t 外积 t = t 外积 R * x1 ;
t外积t =0 sin(cet) =0 垂线段投影 方向垂直两个向量
* x2转置 * t 外积 x2 = x2转置 * t 外积 R x1 = 0 ;
因为 t 外积 x2 得到的向量垂直 t 也垂直 x2
* x2转置 * t 外积 R x1 = x2转置 * E * x1 = 0 ;
得到 x2转置 * E * x1 = 0 , E = t 外积 R 为本质矩阵
* p2转置 * K 转置逆 * t 外积 R * K逆 * p1 = p2转置 * F * p1 = 0 ;
**进一步得到 p2转置 * F * p1 = 0 ,
F = K 转置逆 * t 外积 R * K逆 = K 转置逆 * E * K逆 为基础矩阵**
* x2转置 * E * x1 = 0
* x1 x2 为 由 像素坐标转化的归一化坐标
* x1 = K逆* p1
* x2 = K逆* p2
* p1 、 p2 为匹配点
* 一个点对一个约束 ,8点法 可以算出 E的各个元素
* 再 SVD奇异值分解 E 得到 R t
====================================================================
如果相机移动了足够远,那么就重新创建一个新的关键帧,否则就 匹配当前的关键帧
匹配点对 + 变换矩阵 根据三角测量得到深度
匹配点对使用的方法有:
1. 绝对差和平均值算法(Mean Absolute Differences,简称MAD算法)
2. 绝对误差和算法 (Sum of Absolute Differences,简称SAD算法)
3. 误差平方和平均值算法(Mean Square Differences,简称MSD算法)
4. 误差平方和算法(Sum of Squared Differences,简称SSD算法)
5. 归一化积相关算法(Normalized Cross Correlation,简称NCC算法),
与上面算法相似,依然是利用子图与模板图的灰度,
通过归一化的相关性度量公式来计算二者之间的匹配程度。
1. 用立体视觉方法来从先前的帧得到新的深度估计
2. 深度图帧与帧之间的传播(扩散卡尔曼滤波)
3. 部分规范化已知深度
实际上就是搜索到最先看到这些像素的帧,一直到当前帧的前一帧作为参考帧,
如果搜索失败,说明匹配很差,
那么就增大像素的”年龄”,让它在新的能够看到这些像素的帧里面能够被搜索到。
就实际运作而言,也是分为三大步:
1. 参考帧上极线的计算
2. 极线上得到最好的匹配位置
3. 通过匹配位置计算出最佳的深度
在这个三大步中,
第一步需要得到几何差异误差,
第二步需要得到图像差异误差,
最后一步需要根据极线量化误差
p2' = K × P2 =
fx 0 ux X2 fx * X2 + ux * Z2
0 fy uy × Y2 = fy * Y2 + uy * Z2
0 0 1 Z2 Z2
P2 = K逆 * p2'
p2 = u fx/Z2 * X2 + ux
v = 1/Z * p2' = fy/Z2 * Y2 + uy
1 1
这里的Z2就是 点在投影面p2下的深度
p2' = Z2 * p2 = d * p2
那么 P2 = K逆 * p2' = Z * K逆 * p2 = d * K逆 * p2
P2为相机视角2下的3D坐标, P1为相机视角1下的3D坐标
P2 = R * P1 + t
P1 = R逆 * (P2 - t) =
R逆 * P2 - R逆*t =
R' * P2 + t' =
d * R' * K逆 * p2 + t'
R' = R逆
t' = - R逆*t
P1 = d * R' * x2 + t' , x2 为相机视角2的归一化平面 x2 = K逆 * p2
上式 P1 可由 p1求得部分
x2 可由 p2求得
R' 、 t' 可由 R、t求得
R、t可由第一步 Tracking 跟踪 得到
P1为相机视角1下的3D坐标
p1' = K * P1 =
fx 0 ux X1 fx * X1 + ux * Z1
0 fy uy × Y1 = fy * Y1 + uy * Z1
0 0 1 Z1 Z1
p1 = 1/Z1 * p1'
[P1]1 = d * [R']1 * x2 + [t']1
[P1]2 = d * [R']2 * x2 + [t']2
[P1]3 = d * [R']3 * x2 + [t']3
[P1]1 / [P1]3 = [K逆 * p1]1
[P1]2 / [P1]3 = [K逆 * p1]2
在相机视角2下的像素点p2,如果通过极线搜索匹配找到了一个确定的p1, 这里通过 直接法灰度块匹配
使用p1的横纵坐标均可求得深度d
联立可求解d
由于SLAM领域经过长期实践发现取深度倒数在计算机中表示并对其进行估计有着更高的健壮性,
所以如今的SLAM系统一般使用逆深度对三维世界进行表示。
a) 近似为小基线长度双目,使用对极几何来估计 深度均值;
b) 几何误差和光度误差 估计 深度方差;
===================================================
直接法的SLAM中一般采用迭代优化算法求出图像位姿变换,
此时需要定义误差函数及寻求误差函数对位姿变换的导数,变换到李代数上进行更新后再变换回李群上。
而求解这个问题的方法就是高斯牛顿迭代法的各种变种。
根据上述两步骤 初步得到 变换矩阵T=[R t] 李群 SE(3) 李代数 se(3) 和逆深度 以及深度均值后
我估计看到这里,可能刚刚松了一口气,但是不得不说的是,我们进入了最后一个环节,全局地图优化
它的背景是这样的,单目slam由于它的绝对尺度信息是不能直接得到的(一只眼睛很难确定远近),
导致长距离运动之后,会产生巨大的尺度漂移。为了解决这个问题,我们需要对地图进行全局优化
首先我们需要插图关键帧到地图当中,要插入关键帧,自然需要知道什么时候需要插入,那么我们需要定义一个距离
这里的W是一个对角阵,表示每个维度的权重,我们设定一个阈值,假如 运动距离大于设定的阈值,
那么就需要插入一帧,这个阈值实际上和当前场景有关,
同时我们需要保证它足以满足小基线立体相机的要求。
在插入帧的同时,我们还需要知道两帧之间是如何变换的,由于我们是单目slam,
尺度漂移几乎是不可避免的,因此如果在这么”大”的一个尺度上,还是用se(3),
可能会导致两帧之间的变换不那么准确,因此我们放出一个尺度的自由度,
使用sim(3)来衡量两帧之间的变换,也就是说,我们需要找到一个sim(3)群中的变换kesi,
使得下面定义这个误差最小:
式子中:
匹配点坐标 误差和误差的不确定度 协方差
式子中:
匹配点你深度 误差和误差的不确定度 协方差
那么如何去寻找要插入的位置呢?方法很简单,
首先去寻找所有可能相似的关键帧,并计算视觉意义上的相似度,
之后对这些帧进行排序,得到最相似的那几帧,
然后根据上面那个方程算出sim(3),相似度衡量公式:
如果这个数值足够小(这个相似度足够高),那么这一帧便插入map中,
最后执行图优化(g2o)边为连接关系,节点为关键帧,即优化:
对函数 f(x)一阶泰勒展开得
f(x+Δ)=f(x0) + f′(x0)Δ = f(x0) + (x - x0)*f′(x0) f'(x)为斜率 tan(a) 对边长度 = 斜率×直角边 = f'(x)×Δ
求f(x)=0,得到 f(x0) + (x - x0)*f′(x0) = 0
x = x0 − f(x0) / f′(x0) 不断迭代优化
是函数f(x) 逼近0点附近
f′(x) ≈ f′(x0) + (x-x0)f′′(x0)
令 f′(x0) + (x-x0)f′′(x0) = 0
得到 x = x0 − f'(x0) / f′'(x0) 不断迭代优化,使得 f'(x) 逼近0,使得f(x)达到极值
多维函数的一阶导数F'(X) = J 雅克比矩阵, X = [ x1, x2, x3, x4, ..., xn]
多维函数的二阶导数F''(X) = H 海赛矩阵, X = [ x1, x2, x3, x4, ..., xn]
当对多维函数F(X),进行优化时,原来一维函数优化迭代式子 x = x0 − f'(x0) / f′'(x0)
可写成 X = X0 - F'(X0)/F''(X0)*F(X0)
X = X0 - J/H * F(X0) = X0 - H逆 * J转置 * F(X0)
雅克比矩阵(J) 代替了低维情况中的一阶导,海赛矩阵代替了二阶导,求逆代替了除法。
因为 二阶导数求解太过耗时,使用 雅克比矩阵J来近似海赛矩阵H
H ≈ J转置 * J
得到 X = X0 - H逆 * J转置 * F(X0) = X0 - (J转置 * J)逆 * J转置 * F(X0)
调整 海赛矩阵H 的近似表达式
H ≈ J转置 * J + λI, λ是一个可调参数, I是单位矩阵
莱文贝格-马夸特方法(Levenberg–Marquardt algorithm)能提供数非线性最小化(局部最小)的数值解。
此算法能借由执行时修改参数达到结合高斯-牛顿算法以及梯度下降法的优点,
并对两者之不足作改善(比如高斯-牛顿算法 的逆矩阵不存在 或是 初始值离局部极小值太远)
在高斯牛顿迭代法中,我们已经知道 Δ = − (J转置 * J)逆 * J转置 * F(X0)
X = X0 + Δ = X0 - (J转置 * J)逆 * J转置 * F(X0)
在莱文贝格-马夸特方法算法中则是 Δ = − (J转置 * J + λI )逆 * J转置 * F(X0)
X = X0 + Δ = X0 - (J转置 * J + λI)逆 * J转置 * F(X0)
Levenberg-Marquardt方法的好处就是在于可以调节
如果下降太快,使用较小的λ,使之更接近高斯牛顿法
如果下降太慢,使用较大的λ,使之更接近梯度下降法 Δ = − J转置 * F(X0)
向量 u = (u1, u2, u3)
v = (v1, v2, v3)
两个向量叉乘,得到一个垂直与向量u和向量v组成的平面,
u × v = (u2*v3 - u3*v2 0 -u3 u2 v1
u3*v1 - u1*v3 = u3 0 -u1 * v2
u1*v2 - u2*v1) -u2 u1 0 v3
叉积性质 u × v * u = u × v * v = 0向量, 且 u × v = -v × u
u × v = u' * v, 向量 u 叉乘 上 向量v,可以转化成一个矩阵 与 u的向量乘积
这个矩阵是一个3×3的实数矩阵,叫做 向量u的反对称矩阵,(我的叫法为叉乘矩阵)
0 -u3 u2
u' = u3 0 -u1
-u2 u1 0
注意观察这个矩阵,它有一个特殊的性质
0 u3 -u2
u'转置 = - u' = -u3 0 u1
u2 -u1 0
反对称矩阵性质 A转置 = -A
正交矩阵 性质 B转置 = B逆
旋转矩阵为正交矩阵,
正交矩阵每一列都是单位向量,并且两两正交,
正交矩阵的逆(inverse)等于正交矩阵的转置(transpose)
以三个欧拉角中的RotX为例(其余两个欧拉角以此类推,标准笛卡尔坐标系绕x轴旋转O角都,逆时针旋转为正方向)
1 0 0
Rx = 0 cos sin
0 -sin cos
cos 0 sin
Ry = 0 1 0
-sin 0 cos
cos -sin 0
Rz = sin cos 0
0 0 1
验证,每一列是一个新的坐标系的向量,
第一列为x,第二列为y,第三列为z
可以验证没一列向量的模长为1 cos^2 + sin^2 =1
且列与列相乘为0,即 两两正交
且 转置 = 逆矩阵
R * R逆矩阵 = I单位矩阵 = R * R转置
对上式求导得到 R' * R转置 + R * R'转置 = 0
R' * R转置 = - R * R'转置 = -(R' * R转置)转置
得到 (R' * R转置)转置 = - R' * R转置, R' * R转置 满足 反对称矩阵的性质
所以 R' * R转置 = w 为反对称矩阵
式子两边右乘 R,得到
R' = w * R
存在一个三维向量,其组成的反对称矩阵为 w
一个变量的导数等于它本身再乘以一个系数, exp(a * x)‘ = a * exp(a * x) 指数函数就满足这个性质
1 0 0
如果 R 为单位矩阵 I = 0 1 0
0 0 1
则 R’ = w
单位矩阵(标准笛卡尔坐标系空间)的导数,是一个三维向量W3 (3*1) 组成的反对称矩阵w , (3*3)
这里 3×3 的矩阵表示的是一个空间,空间的 导数 是一个面
类似的 一个二维曲线在某处的导数是一条切线
求得导数之后就可以根据 泰勒展开式,进行近似表达
R(t0 + dt) = R + R'*dt = I + w*dt
李代数 so3
我们把所有的 这些反对称矩阵集合起来就组成了一个所谓的 李代数 Lie algebra so3
李群 SO3
把所有的旋转矩阵集合起来呢,就有了一个所谓的李群Lie group SO(3)
如果 R是单位矩阵,那它的导数就是一个反对称矩阵,所以只有反对称矩阵组成的空间,即 so(3)
我们称之为在在单位矩阵处的正切空间tangent space.
对于三维球面空间,其在某一点的导数,应该是一个切面。
在非单位矩阵的R处的正切空间(导数空间)就是反对称矩阵乘以R
R‘ = w * R
R(t)' = w * R(t)
把旋转矩阵R用x替换掉,如下:
x(t)' = w * x(t), 一个函数的导数 等于一个系数乘以它自身(指数函数 exp(a*t))
求解微分方程的到:
x(t) = exp(w*t)*x(0)
其中 exp(w*t) 是矩阵的指数映射,可以按照泰勒公式展开:
exp(w*t) = I + w*t + (w*t)^2/2! + ... + (w*t)^n/n! + ...
假设 R(0) = I,单位矩阵
R(t) = exp(w*t)
R(t)旋转矩阵,是正交矩阵,满足 转置 = 逆矩阵
可以验证:
(exp(w*t))^(-1) = exp(-w*t)
因为 反对称矩阵w满足 转置 = -本身
(exp(w*t))^(-1) = exp(-w*t) = exp(w转置 * t) = exp(w*t)转置
我们说,可以将 反对称矩阵 w 的 so3李代数 通过 指数映射 (R(t) = exp(w*t)) 转换到 旋转矩阵R 的 SO3李群上去
也即将 三维曲面空间 R 的导数,某点上的切平面上的一点 通过指数映射到 三维曲面空间上去
考虑一种简单情况,当反对称矩阵 对应的 3维向量的模长为1时,||w||=1,旋转速度恒定为1
w
w^2 = w*w
w^3 = w*w*w = -w转置 * w * w = -w
w^4 = -w^2
w^5 = w
w^6 = w^2
w^7 = -w
w^8 = -w^2
w^9 = w
...
exp(w*t) =
I + ( t - t^3/3! + t^5/5! - t^7/7! + t^9/9! - ...)*w +
(t^2/2! - t^4/4! + t^6/6! - t^8/8! + t^10/10! - ...) * w^2
注意括号内的内容分别就是 sin(t) 和 1-cos(t)
exp(wt) = I + sin(t) * w + w^2(1-cos(t))
当然,对于任意的旋转矩阵,我们也能够找到一组对应的W向量(反对称矩阵w) 和 t:
任意:旋转矩阵 R
r11 r12 r13
R = r21 r22 r23
r31 r32 r33
t = arccos((trace(R) - 1)/2) , trace为矩阵的 迹,主对角线元素的和
r32 - r23
W向量 = (W1, W2, W3) = 1/(2*sin(t)) * r13 - r31 和 反对称矩阵位置有关系 正-负
r21 - r12
0 -W3 W2
反对称矩阵 w = W3 0 -W1
-W2 W1 0
上面推导的是连续时间的,并且假设||w||=1,即旋转速度为单位速度,t是一个时间跨度,
联合起来的物理意义就是在单位旋转速度w下,经过时间t后,旋转了多少。
可是,我们常常见到的是另一种情况,单位时间t,旋转速度却不为单位模长了,||w||≠1。
表达成公式就是如下情况:
速度不恒定就需要积分类求得?
exp(w) = I + w + w^2/2! + ... + w^n/n! + ...
= I + SUM(w^(2i+1)/(2i+1)! + w^(2i+2)/(2i+2)!) , 0<= i <无穷大
w*3 = -(W^T * W)*w
cet^2 = W^T * W 向量的模长 ||W|| 变量替换 原先为t
w^(2i+1) = (-1)^i * cet^(2i) * w
w^(2i+1) = (-1)^i * cet^(2i) * w^2
exp(w) = I + SUM(w^(2i+1)/(2i+1)! + w^(2i+2)/(2i+2)!)
= I + SUM((-1)^i * cet^(2i)/(2i+1)! * w + (-1)^i * cet^(2i)/(2i+2)! * w^2)
= I + (1 - cet^2/3! + cet^4/5! - ... )*w + (1/2! - cet^2/4! + cet^4/6! - ... )*w^2
= I + sin(cet) / cet * w + ((1-cos(cet))/cet^2) * w*2
= I + sin(||W||)/||W|| * w + ((1-cos(||W||))/||W||^2) * w*2
这公式就只和W这个三维向量有关了
t = arccos((trace(R) - 1)/2) , trace为矩阵的 迹,主对角线元素的和
r32 - r23
W向量 = (W1, W2, W3) = 1/(2*sin(t)) * r13 - r31 和 反对称矩阵位置有关系 正-负
r21 - r12
0 -W3 W2
反对称矩阵 w = W3 0 -W1
-W2 W1 0
||W||的计算轻松加随意,三维向量变换成反对称矩阵也是容易,所以整个将三维旋转速度映射到旋转矩阵编程实现是不是也很容易了。
求导 T导数* T逆 = [ R导数*R转置 t导数 - R导数*R转置*t,0 0 0 0]
存在一个反对称矩阵 w = R导数*R转置 3*3 实际有效的有三个量 W
和一个三维向量 v = t导数 - w*t 实际有效的有三个量
T导数* T逆 = [ w v,0 0 0 0] = m 实际有效的有六个量
T导数 = m * T
导数知道了
可以对 T 利用泰勒展开进行近似
T(t+dt) = T(t) + m(t) * T(t)dt = (I + m(t) * dt) * T(t)
m 称为 在 曲线 T(t) 处的正切向量
se(3) 刚体变换李代数 就是 m组成的集合
T导数 = m * T
一个函数的导数为 一个系数乘以其自身
则此函数为 指数函数 微分方程求解
T(t) = exp(m*t)*T(0)
m = [ w v,
0 0]
假设 T(0) = I
则
exp(w*t) (I-exp(w*t))*w*v + W * W转置*v*t
T(t) = exp(m*t) = 0 1
将 se(3) 通过指数映射 映射到 SE(3)
去掉 时间t 的版本
指数映射
李群 T = exp(李代数)
T = exp(m) = exp(w.) V*v = R t
0 1 0 1
李代数 m = ln(T) 对数映射
exp(w.) = I + sin(||W||)/||W|| * w + ((1-cos(||W||)) / (||W||^2) ) * w*2
V = I + ((1-cos(||W||))/(||W||^2)) * w + (||W|| - sin(||W||) )/(||W||^3) * w^2
t = t1 t2 t3 平移向量
v = t导数 - w*t
任意:旋转矩阵 R
r11 r12 r13
R = r21 r22 r23
r31 r32 r33
t = arccos((trace(R) - 1)/2) , trace为矩阵的 迹,主对角线元素的和
r32 - r23
W向量 = (W1, W2, W3) = 1/(2*sin(t)) * r13 - r31 和 反对称矩阵位置有关系 正-负
r21 - r12
0 -W3 W2
反对称矩阵 w = W3 0 -W1
-W2 W1 0
各种论文里涉及到的求解位姿矩阵时的非线性最小二乘优化(牛顿法,LM法),
其中增量都是在单位矩阵处的tangent space se(3)上计算,
获得的增量(即相邻位姿变换关系)通过指数映射映射回多面体SE(3)上。
通过这种方式,能够避免奇异点,保证很小的变换矩阵也能够表示出来。
* 本库为旧版本 非模板的版本
* git clone https://github.com//strasdat/Sophus.git
* git checkout a621ff 版本
* 再cmake编译
SO(n) 特殊正交群 对应 n*n 的旋转矩阵 R 群(集合)
SE(n+1) 特殊欧式群 对应 n*n 的旋转矩阵和 n*1的平移向量 组合成的 变换矩阵T 群(集合)
so(n) SO(n)对应的李代数 为 so(n) n×n矩阵 3×3时实际有效向量为 3个 4*4是实际有效向量为3+3=6个
使得矩阵 和 代数 一一对应 可以使用代数的更新方法来更新 矩阵
SO(3) 表示三维空间的 旋转矩阵 集合 R 3×3
SE(3) 表示三维空间的 变换矩阵 集合 T 4×4
李代数 so3的本质就是个三维向量,直接Eigen::Vector3d定义(简化表示),
实际是由这三维向量对应的反对称矩阵
李代数 se3的本质就是个六维向量,3个旋转 + 3个平移,
实际是一个4*4的矩阵,可有效向量数量为6个
任意:旋转矩阵 R 平移向量 t
r11 r12 r13
R = r21 r22 r23
r31 r32 r33
cet = arccos((trace(R) - 1)/2) , trace为矩阵的 迹,主对角线元素的和
r32 - r23
W向量(so3本质的三维向量) = (W1, W2, W3) = 1/(2*sin(cet)) * r13 - r31
r21 - r12
和 反对称矩阵位置有关系 正-负
0 -W3 W2
反对称矩阵 w = W3 0 -W1 这个反对称矩阵实际为 so3
-W2 W1 0
se3 m = [ w v, 4*4的矩阵 实际有效变量有 3+3 六个
0 0]
v = t导数 - w*t
1. 旋转向量 Eigen::AngleAxisd 角度 + 轴
Eigen::AngleAxisd rotation_vector ( M_PI/4, Eigen::Vector3d ( 0,0,1 ) );//沿 Z 轴旋转 45 度
2. 旋转矩阵 Eigen::Matrix3d 3*3 R
rotation_vector.toRotationMatrix(); //旋转向量转换 到 旋转矩阵
// 旋转向量 直接转 旋转矩阵
Eigen::Matrix3d Eigen::Matrix3d R =
Eigen::AngleAxisd(M_PI/2, Eigen::Vector3d(0,0,1)).toRotationMatrix();
3. 欧拉角向量 Eigen::Vector3d 3*1 r, p, y
Eigen::Vector3d rotation_matrix.eulerAngles ( 2,1,0 );
// ( 2,1,0 )表示ZYX顺序,即roll pitch yaw顺序 旋转矩阵到 欧拉角转换到欧拉角
4. 四元素 Eigen::Quaterniond
Eigen::Quaterniond q = Eigen::Quaterniond ( rotation_vector );// 旋转向量 定义四元素
q = Eigen::Quaterniond ( rotation_matrix ); //旋转矩阵定义四元素
5. 欧式变换矩阵 Eigen::Isometry3d 4*4 T
Eigen::Isometry3d T=Eigen::Isometry3d::Identity();
// 虽然称为3d,实质上是4*4的矩阵 旋转 R+ 平移t
T.rotate ( rotation_vector ); // 按照rotation_vector进行旋转
也可 Eigen::Isometry3d T(q) // 一步 按四元素表示的旋转 定义 变换矩阵
T.pretranslate ( Eigen::Vector3d ( 1,3,4 ) );// 把平移向量设成(1,3,4)
cout<< T.matrix() <<endl;
1. 旋转向量定义的 李群SO(3)
Sophus::SO3 SO3_v( 0, 0, M_PI/2 );
// 亦可从旋转向量构造 这里注意,不是旋转向量的轴,是对应轴 + 轴上的旋转
相当于把轴 和 旋转角度 放在一起表示了 (0, 0, M_PI/2) 表示的就是 绕 Z轴(0,0,1), 旋转M_PI/2角度
2. 旋转向量 转 旋转矩阵 角 Z轴(0,0,1)
Eigen::Matrix3d R = Eigen::AngleAxisd(M_PI/2, Eigen::Vector3d(0,0,1)).toRotationMatrix();
3. 旋转矩阵定义的 李群SO(3)
ophus::SO3 SO3_R(R); // Sophus::SO(3)可以直接从旋转矩阵构造
4. 旋转矩阵 转 四元素
Eigen::Quaterniond q(R); // 或者四元数(从旋转矩阵构造)
5. 四元素定义的 李群SO(3)
Sophus::SO3 SO3_q( q );
6. 李代数so3 为李群SO(3) 的对数映射
Eigen::Vector3d so3 = SO3_R.log();
7. 平移 向量表示
Eigen::Vector3d t(1,0,0); // 沿X轴平移1
8. 从旋转矩阵R 和 平移t 构造 欧式变换矩阵李群 SE3
Sophus::SE3 SE3_Rt(R, t); // 从R,t构造SE(3)
9. 从四元素q和 平移t 欧式变换矩阵李群 SE3
Sophus::SE3 SE3_qt(q,t); // 从q,t构造SE(3)
10. 李代数se(3) 是一个6维向量 为李群SE3 的对数映射
typedef Eigen::Matrix<double,6,1> Vector6d;// Vector6d指代 Eigen::Matrix<double,6,1>
Vector6d se3 = SE3_Rt.log();
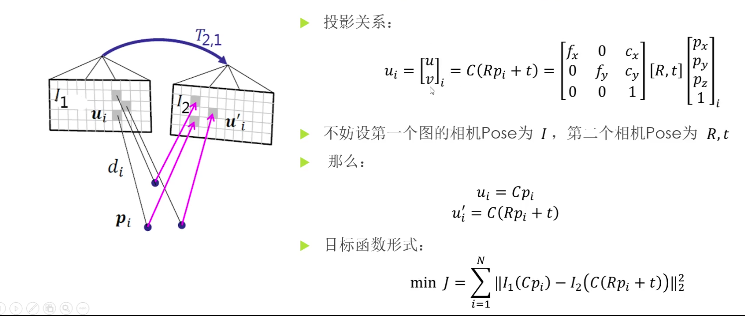
将一个图像中的二维像素点根据相机内参数和深度信息投影到三维空间,
再通过欧式变换关系[R t]变换到另一个图像的坐标系下,
再通过相机内参数投影到其像素平面上。
可以求的的误差,使用优化算法,更新[R t]来使得误差最小
当把 三维点Pi 也作为优化参数时,可以这样考虑
图像1 像素点 p = {p1,p2,p3,...,pn} qi = [u,v]
图像2 像素点 q = {q1,q2,q3,...,qn}
物理空间3D点 P = {P1,P2,P3,...,Pn} 坐标系为图像1的坐标系 Pi = [X,Y,Z]
相机内参数
K = [fx, 0, ux
0, fy, uy
0, 0, 1]
K_inv = [f1/x, 0, -ux
0, 1/fy, -uy
0, 0, 1]
则有:
3D点 Pi 投影到 图像1的像素坐标系下
K*Pi = fx*X + Z*ux x1 d1*u'
fy*Y + Z*uy = y1 = d1 * pi' = d1*v' d1为3D点在图像1下的深度
Z z1 d1
u'
投影点pi' v' = 1/d1 * K*Pi 值 约接近 pi 误差越小
1
3D点 Pi 投影到 图像2的像素坐标系下:
K*(R*Pi+t)= x2
y2 = d2 * qi'
z2
投影点 qi' = 1/d2 * K*(R*Pi+t) d2为3D点在图像2下的深度
理论上使用 8个匹配点对就可以求解
可以使用RanSac 随机序列采样一致性方法获取更鲁棒的解 [R,t]
使用 差平方和作为 误差函数:
E = sum( (1/d1 * K*Pi - [pi,1])^2 + (1/d2 * K*(R*Pi+t) - [qi,1]^2) )
求解Pi,R,t 使得 E最小
它叫做最小化重投影误差问题(Minimization of Reprojection error)。
在实际操作中,我们实际上是在调整每个 Pi,使得它们更符合每一次观测值pi和qi,
也就是使每个误差项都尽量的小,
由于这个原因,它也叫做捆集调整(Bundle Adjustment)。
上述方程是一个非线性函数,该函数的额最优化问题是非凸的优化问题,
求解E的极值,当E的导数为0时,取得
那么如何使得 E的导数 E'=0呢?
对 E' 进行 泰勒展开
一阶泰勒展开 :
E'(x) = E'(x0) + E''(x0) * dx
= J + H * dx = 0
而:
dx = -H逆 * J转置 * E(x0)
也可以写成:
H * dx = -J转置 * E(x0)
求解时,需要求得函数 E 对每一个优化变量的
偏导数形成偏导数矩阵(雅克比矩阵)J
二阶偏导数求解麻烦使用一阶偏导数的平方近似代替
H = J转置*J
可以写成如下线性方程:
J转置*J * dx = -J转置 * E(x0)
这里 误差E(x0)可能会有不同的置信度 可以在其前面加一个权重 w
J转置*J * dx = -J转置 * w * E(x0)
A * dx = b GS高斯牛顿优化算法
(A + λI) = b LM 莱文贝格-马夸特方法 优化算法
Levenberg-Marquardt方法的好处就是在于可以调节
如果下降太快,使用较小的λ,使之更接近高斯牛顿法
如果下降太慢,使用较大的λ,使之更接近梯度下降法 Δ = − J转置 * F(X0)
这里线性方程组的求解 多使用 矩阵分解的算法 常见 LU分解、LDLT分解和Cholesky分解、SVD奇异值分解等
所以这里需要:
1. 系数矩阵求解器,来求解 雅可比矩阵J 和 海塞矩阵H, BlockSolver;
2. 数值优化算法 GS高斯牛顿优化算法/LM 莱文贝格-马夸特方法 优化算法
计算 A / (A + λI)
3. 线性方程求解器,从 PCG, CSparse, Choldmod中选
g2o 全称 general graph optimization,是一个用来优化非线性误差函数的c++框架。
稀疏优化 SparseOptimizer 是我们最终要维护的东东。
它是一个Optimizable Graph,从而也是一个Hyper Graph。
一个 SparseOptimizer 含有很多个顶点 (都继承自 Base Vertex)和
很多种边(继承自 BaseUnaryEdge, BaseBinaryEdge或BaseMultiEdge)。
这些 Base Vertex 和 Base Edge 都是抽象的基类,而实际用的顶点和边,都是它们的派生类。
我们用
SparseOptimizer.addVertex 和
SparseOptimizer.addEdge 向一个图中添加顶点和边,
最后调用 SparseOptimizer.optimize 完成优化。
在优化之前,需要指定我们用的求解器和迭代算法。
一个 SparseOptimizer 拥有一个
迭代算法 Optimization Algorithm,
继承自Gauss-Newton, Levernberg-Marquardt, Powell's dogleg 三者之一(我们常用的是GN或LM)。
同时,这个 Optimization Algorithm 拥有一个 Solver,它含有两个部分:
1. 一个是 SparseBlockMatrix ,用于计算稀疏的雅可比和海塞,BlockSolver;
2. 一个是用于计算迭代过程中最关键的一步,线性方程组求解器;
H * Δx = −b
这就需要一个线性方程的求解器。
而这个求解器,可以从 PCG, CSparse, Choldmod 三者选一。
综上所述,在g2o中选择优化方法一共需要三个步骤:
1. 选择一个线性方程求解器,从 PCG, CSparse, Choldmod中选,实际则来自 g2o/solvers 文件夹中定义的东东。
2. 选择一个 BlockSolver 。
3. 选择一个迭代优化更新策略,从GN, LM, Doglog中选。
* 每张图像创建 5层的图像金字塔 每一层的尺度 变为上一层的1/2
* 图像的 内参数 也上上一层的 1/2
* 内参数求逆得到 内参数逆矩阵
* 一帧包含 Ki = [Ii,Gi,Mi,Di,Vi]
* [像素 梯度 最大梯度值 逆深度 逆深度方差]
* 最大梯度 阈值滤波得到 关键点 需要跟踪 并需要计算三维点映射到地图中
* 上一层 的 四个像素的值的平均值合并成一个像素为下一层的像素
*
* int wh = width*height;// 当前层 像素总数
* const float* s;
* for(int y=0; y<wh; y += width*2)// 隔行
* {
* for(int x=0; x<width; x+= 2)// 隔列下采样
* {
* s = source + x + y;// 上一层 像素对应位置
* *dest = (s[0] +
* s[1] +
* s[width] +
* s[1+width]) * 0.25f;// 四个像素的值的平均值合并成一个
* dest++;
* }
* }
*
* 使用同一层的 图像 左右像素求得x方向梯度 上下求得 方向梯度
* *(img_pt-width)
* val_m1 *(img_pt) val_p1
* *(img_pt+width)
* 1. (val_p1 - val_m1)/2 = x 方向梯度
* 2. 0.5f*(*(img_pt+width) - *(img_pt-width)) = y方向梯度
* 3. val_00 = *(img_pt) 当前 点像素值
* 4. 第四维度 没有存储数据 gradxyii_pt Eigen::Vector4f
*
*
* 创建 梯度图内 临近四点中梯度最大值 的 最大值梯度 图 , 并记录梯度值较大的可以映射 成 地图点的数量
* 在梯度图中 求去合成梯度 g=sqrt(gx^2+gy^2) ,求的 上中下 三个梯度值中的最大值,形成临时梯度最大值图
* 在临时梯度最大值图 中求 的 左中右 三个梯度值中的最大值,形成最后的 最大梯度值地图
* 并记录 最大梯度大小超过阈值的点 可以映射成地图点
*
* 1. 使用 真实 深度值 取反得到逆深度值,方差初始为一个设定值
* 2. 没有真实值是,也可以使用高斯分布均值初始化 逆深度均值图 和方差图
*
*
* 根据逆深度 构建 逆深度均值图 方差图(高斯分布) 金字塔
* current -----> 右边一个
* 下边 下右边 上一层四个位置
* 上一层 逆方差和 / 上一层 逆深度均值 (四个位置处) 和 得到深度信息 再 取逆得到 逆深度均值
* 上一层 逆深度 方差和 取逆得到 本层 逆深度方差
这里 是 SE3跟踪求解 欧式变换矩阵求解
* LSD-SLAM在位姿估计中采用了直接法,也就是通过最小化光度误差来求解两帧图像间的位姿变化。
* 并且采用了LM算法迭代求解。
* 误差函数 E(se3) = SUM((Iref(pi) - I(W(pi,Dref(pi),se3))^2)
* (参考帧下的像素值-参考帧3d点变换到当前帧下的像素值)^2
* 也就是 所有匹配点 的光度误差和
* LSD-SLAM在求解两帧图像间的SE3变换主要在SE3Tracker类中进行实现。
* 1. 首先在参考帧下根据深度信息计算出3d点云
* 2. 其次,计算参考帧下的点变换到当前帧下的亚像素像素值,进而计算初始 光度匹配误差err
* 3. 再次,利用误差对单个3d点的导数信息计算单个误差的可信程度,进行加权后方差归一化,
* 得到权重w,为了减少外点(outliers)对算法的影响
* 4. 然后,利用误差函数对误差向量求导数,求得各个点的误差之间的协方差矩阵,
也是雅克比矩阵J,计算系数A 和 b
* 5. 最后计算 变换矩阵 se3的 更新量 dse3
* dse3 = -(J转置*J)逆矩阵*J转置*w*err 直接求逆矩阵计算量较大
* 也可以写成:
* J转置*J * dse3 = -J转置*w*error
* 紧凑形式:
* A * dse3 = b
* 使用 LDLT分解 A = LDU=LDL转置=LDLT,求解线性方程组 A * x = b
* 记录 u = LD, D为对角矩阵 L为下三角矩阵 L转置为上三角矩阵
* v = L转置
* 将A分解为上面两个矩阵 相乘 A = u * v
* Ax = b就可以化为u(v*x) = u*y = b
* 先求解 y
* 得到 y = v*x
* 再求解 x 即 dse3 是欧式变换矩阵se3的更新量
*
* 6. 然后对 变换矩阵 左乘 se3指数映射 进行 更新
* se3 指数映射到SE3 通过 李群乘法直接 对 变换矩阵 左乘更新
* 1. SE3Tracker::trackFrame 主调函数
* 2. SE3Tracker::calcResidualAndBuffers 被调用计算
* 初始误差 err 参考帧3d点变换到当前帧图像坐标系下的残差(灰度误差) 和 梯度(对应点像素梯度)
* 3. SE3Tracker::calcWeightsAndResidual 被调用计算
* 误差可信度权重w 并对误差方差归一化得到加权平均后的误差
* 4. SE3Tracker::calculateWarpUpdate 被调用计算
* 误差关系矩阵 协方差矩阵 雅克比矩阵J 以及A=J转置*J b=-J转置*w*error 求接线性方程组
* 图像金字塔迭代level-4到level-1
* Step1: 对参考帧当前层构造点云(reference->makePointCloud)
* 利用逆深度信息 和 相应的像素坐标 以及相机内参数得到 在参考帧坐标下的3d点
* (X,Y,Z) = D * (u,v,1)*K逆 =1/(1/D)* (u*fx_inv + cx_inv, v+fy_inv+cy_inv, 1)
* Step2: 计算变换到当前帧的残差和梯度(calcResidualAndBuffers)
* 计算参考帧3d点变换到当前帧图像坐标系下的残差(灰度误差) 和 梯度(对应点像素梯度)
* 1. 参考帧3d点 R,t变换到 当前相机坐标系下
* Eigen::Matrix3f rotMat = referenceToFrame.rotationMatrix();// 旋转矩阵
* Eigen::Vector3f transVec = referenceToFrame.translation();// 平移向量
* Eigen::Vector3f Wxp = rotMat * (*refPoint) + transVec;// 欧式变换
* 2. 再 投影到 当前相机 像素平面下
* float u_new = (Wxp[0]/Wxp[2])*fx_l + cx_l;// float 浮点数类型
* float v_new = (Wxp[1]/Wxp[2])*fy_l + cy_l;
* 3. 根据浮点数坐标 四周的四个整数点坐标的梯度 使用位置差加权进行求和得到亚像素灰度值 和 亚像素 梯度值
* x=u_new;
* y=v_new;
* int ix = (int)x;// 取整数 左上方点
* int iy = (int)y;
* float dx = x - ix;// 差值
* float dy = y - iy;
* float dxdy = dx*dy;
* // map 像素梯度 指针
* const Eigen::Vector4f* bp = mat +ix+iy*width;// 左上方点 像素位置 梯度的 指针
* // 使用 左上方点 右上方点 右下方点 左下方点 的灰度梯度信息
* // 以及 相应位置差值作为权重值 线性加权获取 亚像素梯度信息
* resInterp=dxdy * *(const Eigen::Vector3f*)(bp+1+width)// 右下方点
* + (dy-dxdy) * *(const Eigen::Vector3f*)(bp+width)// 左下方点
* + (dx-dxdy) * *(const Eigen::Vector3f*)(bp+1)// 右上方点
* + (1-dx-dy+dxdy) * *(const Eigen::Vector3f*)(bp);// 左上方点
*
* 需要注意的是,在给梯度变量赋值的时候,这里乘了焦距
* 这里求得 亚像素梯度之后 又乘上了 相机内参数,因为在求 误差偏导数时需要 需要用到 dx*fx dy*fy
* *(buf_warped_dx+idx) = fx_l * resInterp[0];// 当前帧匹配点亚像素 梯度 gx = dx*fx
* *(buf_warped_dy+idx) = fy_l * resInterp[1];// 匹配点亚像素 梯度 gy = dy*fy
* *(buf_warped_residual+idx) = residual;// 对应 匹配点 像素误差
* 这里的 dx= resInterp[0], dy = resInterp[0] 亚像素梯度
*
* (buf_d+idx) = 1.0f / (*refPoint)[2]; // 参考帧 Z轴 倒数 = 参考帧逆深度
* *(buf_idepthVar+idx) = (*refColVar)[1];// 参考帧逆深度方差
* 4. 记录变换
* a. 对参考帧灰度 进行一次仿射变换后 和 当前帧亚像素灰度做差得到 残差(灰度误差)
* 现在求得的残差只是纯粹的光度误差
* float c1 = affineEstimation_a * (*refColVar)[0] + affineEstimation_b;// 参考帧 灰度[0] 仿射变换后
* float c2 = resInterp[2];// 当前帧 亚像素 第三维度是图像 灰度值
* float residual = c1 - c2;// 匹配点对 的灰度 误差值
*
* 疑问1:代码中对参考帧的灰度做了一个仿射变换的处理,这里的原理是什么?
* 在SVO代码中的确有考虑到两帧见位姿相差过大,因此通过在空间上的仿射变换之后再求灰度的操作。
* 但是在这里的代码中没有看出具体原理。
* b. 对两帧下 3d点坐标的 Z轴深度值 的变化比例
* float depthChange = (*refPoint)[2] / Wxp[2];
* usageCount += depthChange < 1 ? depthChange : 1;// 记录深度改变的比例
* c. 匹配点总数
* buf_warped_size = idx;// 匹配点数量= 包括好的匹配点 和 不好的匹配点 数量
* Step3: 计算 方差归一化加权残差和 使用误差方差 对 误差归一化 后求和 (calcWeightsAndResidual)
* 计算误差权重,归一化方差以及Huber-weight,最终把这个系数存在数组 buf_weight_p 中
* 每个像素点都有一个光度匹配误差,而每个点匹配的可信度根据其偏导数可以求得,
* 加权每一个误差 然后求所有点 光度匹配误差的均值
* 误差导数 drpdd = dr= -(dx*fx * (tx*z' - tz*x')/(z'^2*d) + dy*fy * (ty*z' - tz*y')/(z'^2*d))
* = -(gx * (tx*z' - tz*x')/(z'^2*d) + gy * (ty*z' - tz*y')/(z'^2*d))
* dx, dy 为参考帧3d点映射到当前帧图像平面后的梯度
* fx, fy 相机内参数
* tx,ty,tz 为参考帧到当前帧的平移变换(忽略旋转变换)
t = translation()
* x',y',z' 为参考帧3d点变换到当前帧坐标系下的3d点
x' = Wxp[0] , y' = Wxp[1] , z' = Wxp[2]
* d = d = *(buf_d) 为参考帧3d点在参考帧下的逆深度
* gx = *(buf_warped_dx)
* gy = *(buf_warped_dy)
* 方差平方 float s = settings.var_weight * *(buf_idepthVar+i);// 参考帧 逆深度方差 平方
* 误差权重为加权方差平方的倒数 float w_p = 1.0f / ((cameraPixelNoise2) + s * drpdd * drpdd);// 误差权重 方差倒数
* 初步误差 rp =*( buf_warped_residual) ; //初步误差
* 加权的误差 float weighted_rp = fabs(rp*sqrtf(w_p));// |r|加权的误差
* Huber-weight权重
* float wh = fabs(weighted_rp < (settings.huber_d/2) ? 1 : (settings.huber_d/2) / weighted_rp);
* 记录 *(buf_weight_p+i) = wh * w_p; // 乘上 Huber-weight 权重 得到最终误差权重避免外点的影响
* 求和 sumRes += wh * w_p * rp*rp; // 加权误差和
* 取均值 return sumRes / buf_warped_size;// 返回加权误差均值
lastErr = sumRes / buf_warped_size;
* Step4: 计算雅克比向量以及A和b(calculateWarpUpdate)
* J转置*J * dse3 = -J转置*w*lastErr
* 对于参考帧中的一个3D点pi位置处的残差求雅可比,这里需要使用链式求导法则
* Ji = 1/z'*dx*fx + 0* dy *fy
* 0* dx *fx + 1/z' *dy *fy
* -1 * -x'/z'^2 *dx*fx - y'/z'^2 *dy*fy
* -x'*y'/z'^2 *dx*fx - (1+y'^2/z'^2) *dy*fy
* (1+x'^2/z'^2)*dx*fx + x'*y'/z'^2*dy*fy
* - y'/z' *dx*fx + x'/z' * dy*fy
*
* A = J *J转置*(*(buf_weight_p+i))
* b = -J转置*(*(buf_weight_p+i))*lastErr
*
* Step5: 计算得到收敛的delta,并且更新SE3(dse3 = A.ldlt().solve(b))
* for(int i=0;i<6;i++) A(i,i) *= 1+LM_lambda;// (A+λI) 列文伯格马尔夸克更新算法 LM 调整量
* Vector6 inc = A.ldlt().solve(b);// LDLT矩阵分解求解 dse3 李代数更新量
Sophus::SE3f new_referenceToFrame = Sophus::SE3f::exp((inc)) * referenceToFrame;
*
* 重复Step2-Step5直到收敛或者达到最大迭代次数
*
* 计算下一层金字塔