A specification of the Cigarette smokers problem. The generated state graph is very small:
Simple spec simulating, more or less, this application.
Three state machines controlling three LEDs. With 100ms resolution (model run with BC <- <<3, 5, 7>>) model checker
finds 384 distinct states:
Just a humble reminder to never underestimate even the simplest concurrent programs, I guess 😃
All the 'attractors' for a 3x3 grid
State space for a 4x4 grid - original image generated by Graphviz is around 300MB 😃:
The same with some colors based on number of occupied cells:
Zoom on two of the smaller clusters:
Under 'symmetry group of the square' (D4) view in TLC the state space shrinks to ... 27 states. Under this view it's even possible to run TLC on 5x5 grid and get 486 states (reduction from 33554432):
Base Graphviz parameters:
dot -Tpng -Nstyle=filled -Npenwidth=5 -Epenwidth=8 -Ksfdp -Goverlap=prism -Goverlap_scaling=-10Experimental specification aimed at mechanising verification of written requirements documents.
Checking CheckRequirements spec produces:
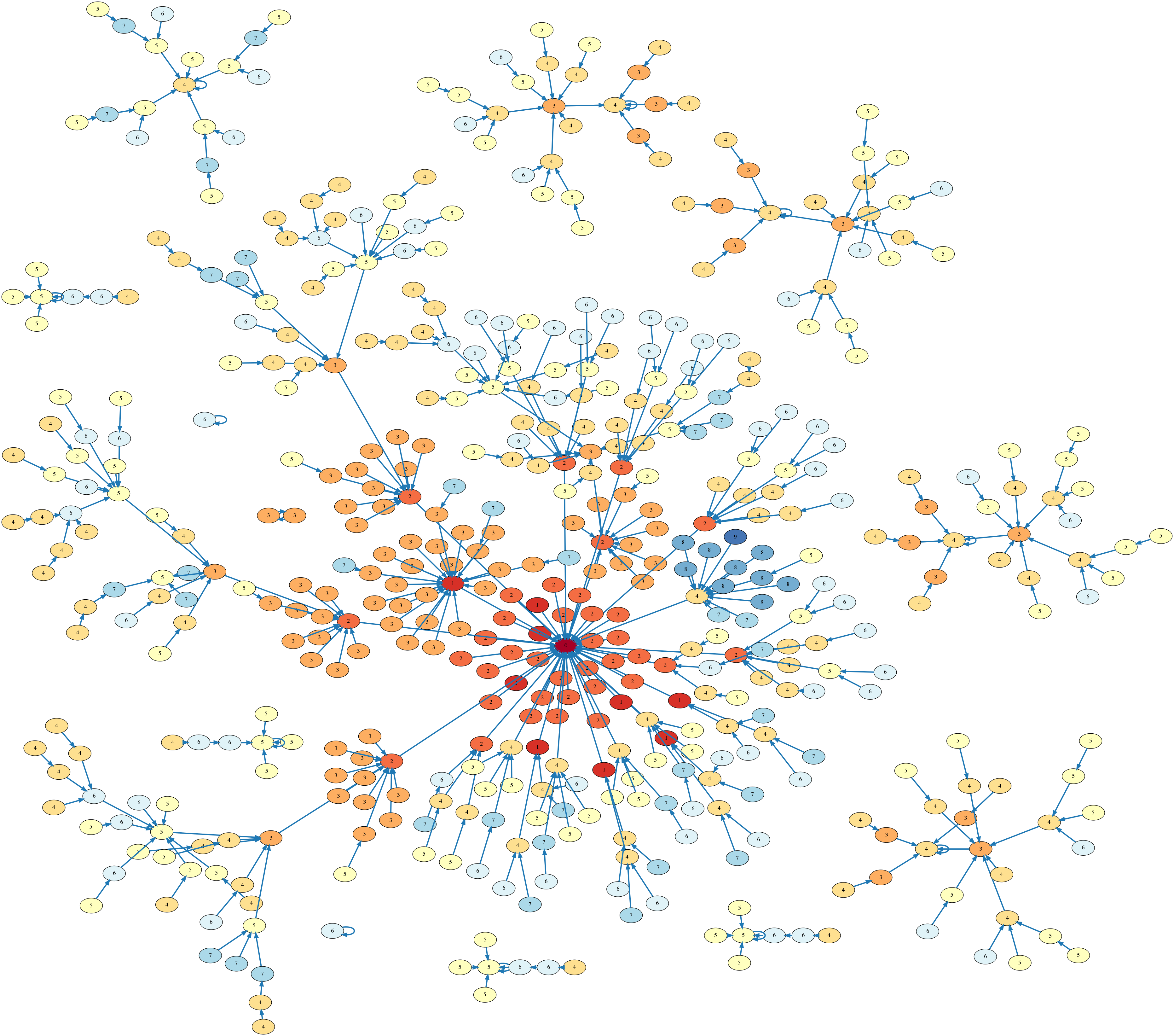
Solution to a variation of sliding block puzzle most commonly known as Klotski.
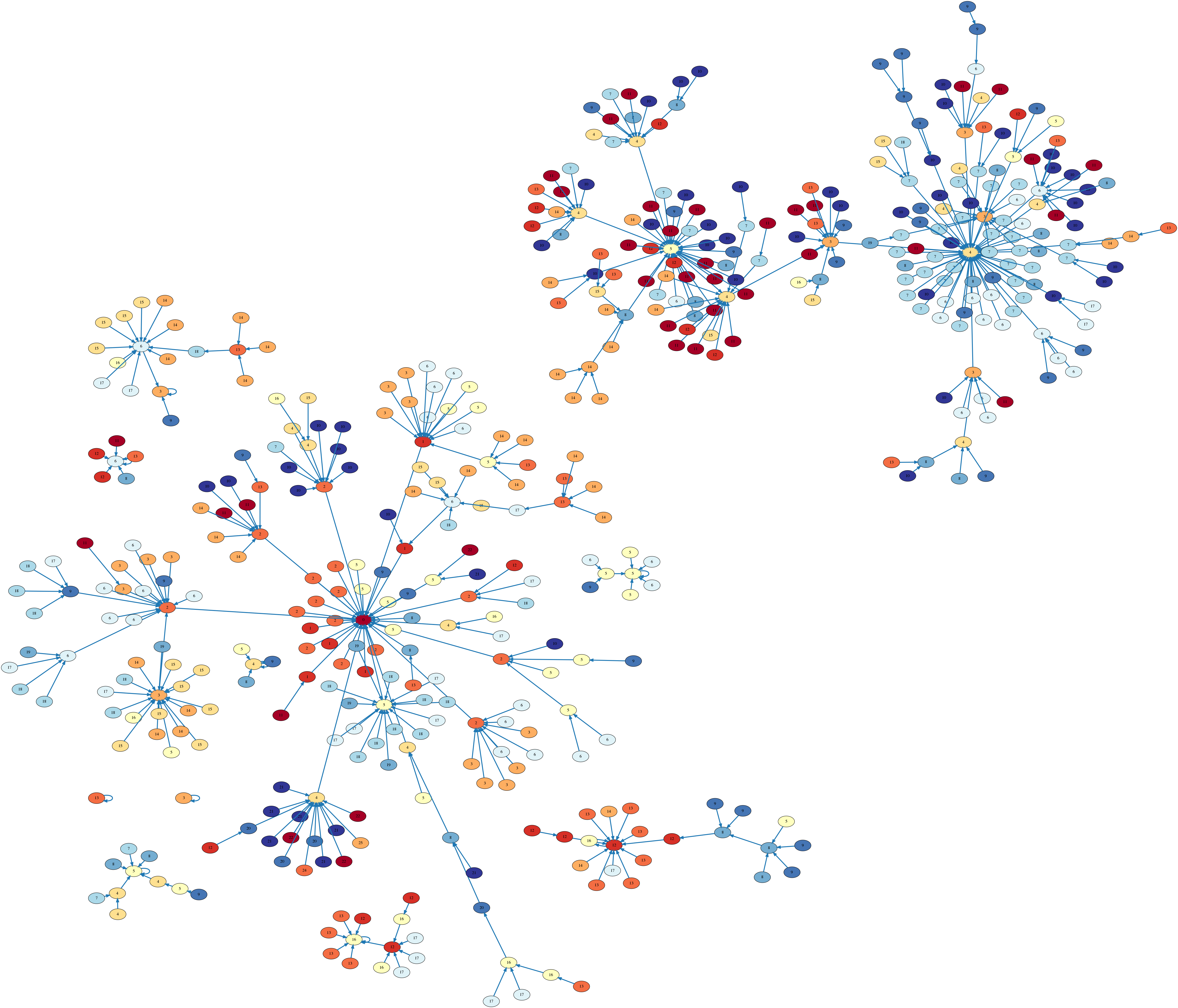
TLC finds 25955 distinct states. Green node is the starting position. Red nodes are the goal nodes - with the biggest piece in center-bottom position.
The Pennant variation has significantly smaller state space of 'only' 1398 states. Raymond Hettinger talked about this puzzle and the state graph here.
W == 4 H == 5
Pennant == {{<<0, 0>>, <<0, 1>>, <<1, 0>>, <<1, 1>>},
{<<2, 0>>, <<3, 0>>}, {<<2, 1>>, <<3, 1>>},
{<<0, 2>>}, {<<1, 2>>},
{<<0, 3>>, <<0, 4>>}, {<<1, 3>>, <<1, 4>>},
{<<2, 3>>, <<3, 3>>}, {<<2, 4>>, <<3, 4>>}}
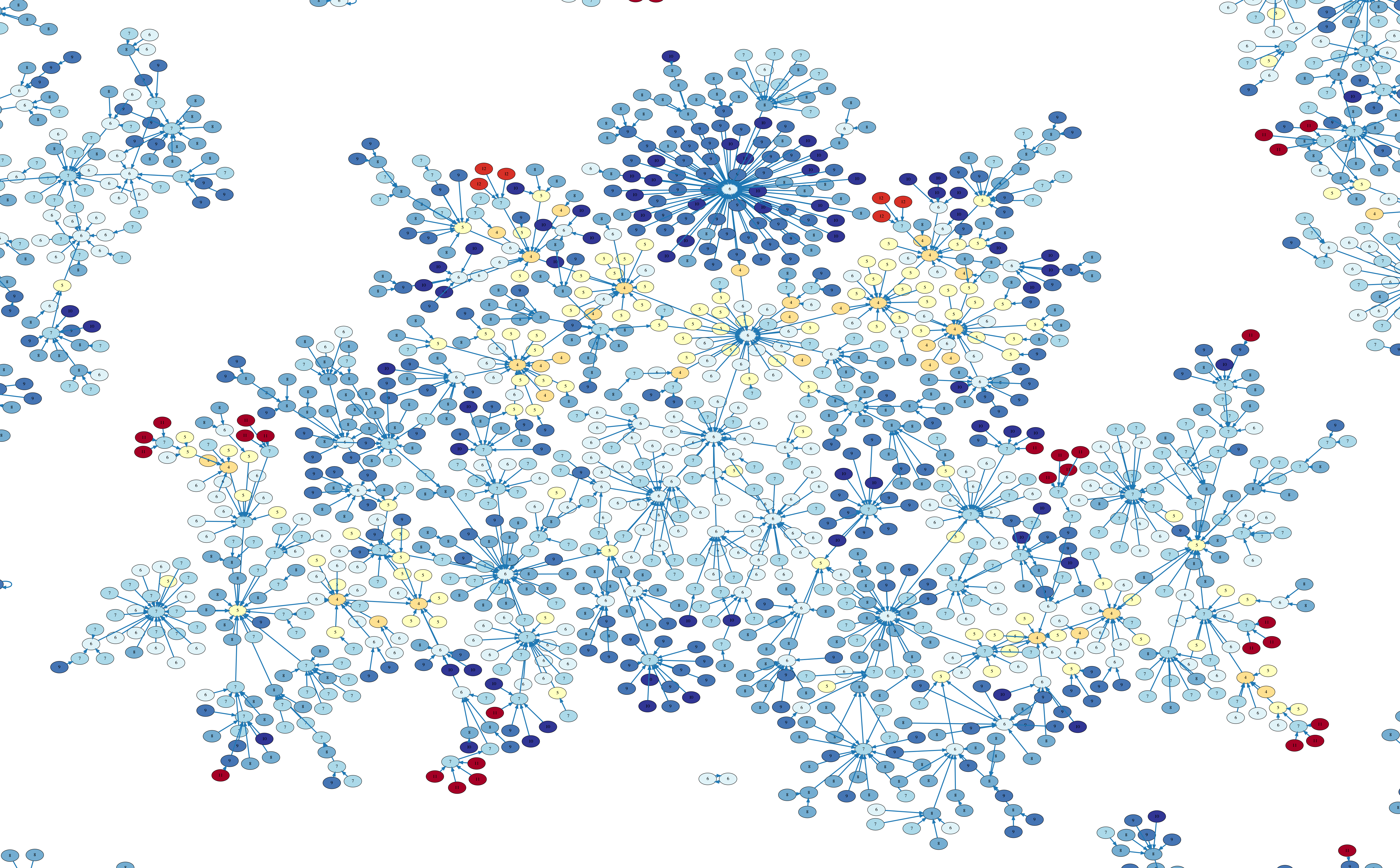
PennantGoal == {<<0, 3>>, <<0, 4>>, <<1, 3>>, <<1, 4>>} \in boardMa's Puzzle has 110804 distinct states.
W == 5 H == 5
Mas == {{<<0, 0>>, <<1, 0>>, <<2, 0>>},
{<<3, 0>>, <<4, 0>>,<<4, 1>>},
{<<0, 1>>, <<1, 1>>}, {<<2, 1>>, <<3, 1>>},
{<<0, 2>>, <<0, 3>>, <<1, 3>>},
{<<1, 2>>, <<2, 2>>}, {<<3, 2>>, <<4, 2>>},
{<<2, 3>>, <<3, 3>>, <<4, 3>>},
{<<2, 4>>}}
MasGoal == {{<<3, 0>>, <<4, 0>>,<<4, 1>>}, {<<3, 1>>, <<3, 2>>, <<4, 2>>}} \subseteq boardA specification of a 'concurrency game' requiring concurrent and symmetrical cooperation - link
For N=3 there are 522 distinct states:
The lattices at the edges are due to the possible orders in which the chameneoses fade.
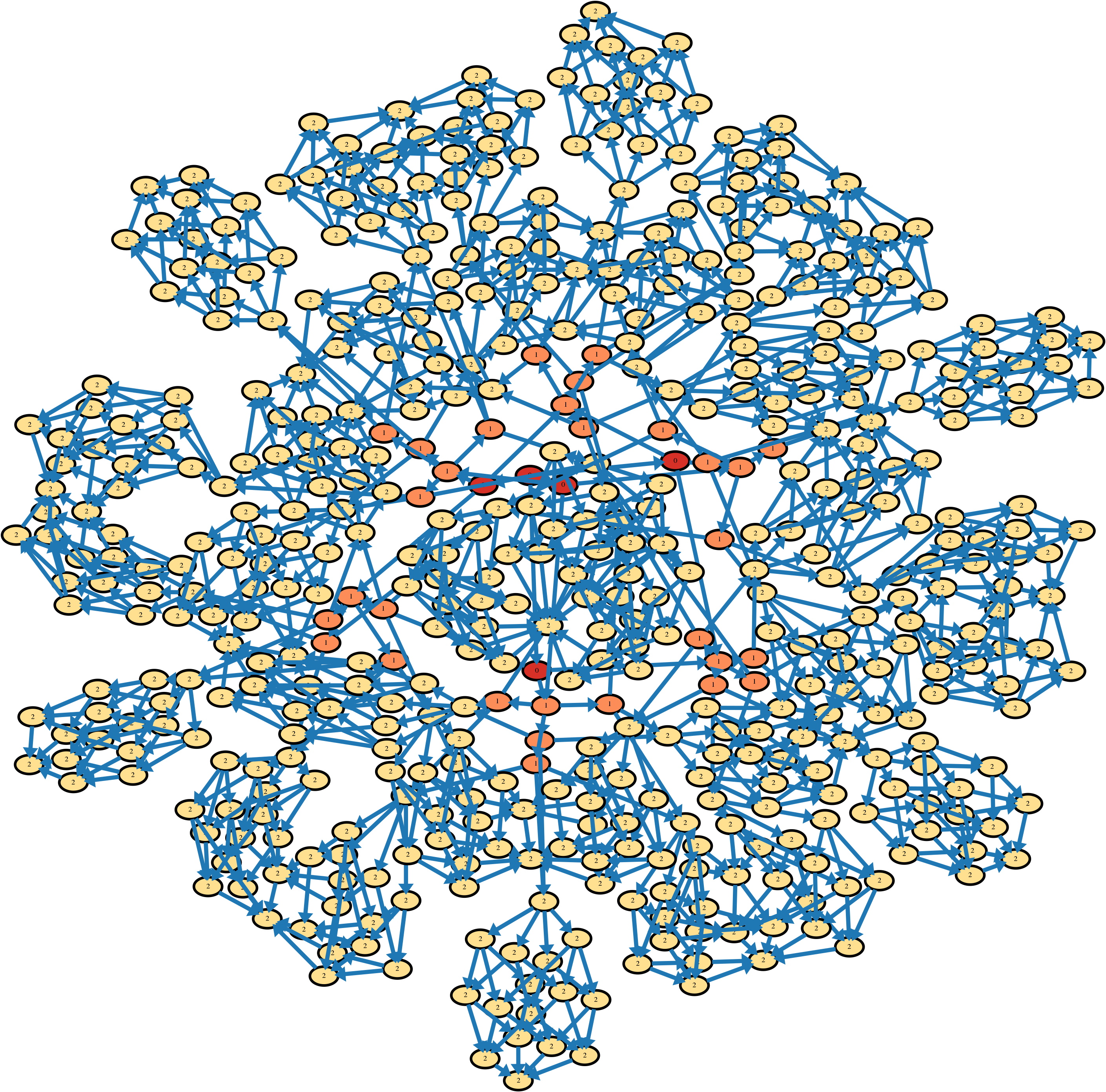
For N=4 there are 6652 distinct states:
All the above graphs are for single initial permutation of chameneoses. Here is a full graph for N=2, M=4 (4843 distinct states).
State diagram for 3-task configuration:
Sample trace rendered graphically. Can you spot when the sequence starts repeating?