欢迎大家参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
题目链接:https://leetcode-cn.com/problems/delete-operation-for-two-strings/
给定两个单词 word1 和 word2,找到使得 word1 和 word2 相同所需的最小步数,每步可以删除任意一个字符串中的一个字符。
示例:
输入: "sea", "eat"
输出: 2
解释: 第一步将"sea"变为"ea",第二步将"eat"变为"ea"
本题和动态规划:115.不同的子序列相比,其实就是两个字符串可以都可以删除了,情况虽说复杂一些,但整体思路是不变的。
这次是两个字符串可以相互删了,这种题目也知道用动态规划的思路来解,动规五部曲,分析如下:
- 确定dp数组(dp table)以及下标的含义
dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最少次数。
这里dp数组的定义有点点绕,大家要撸清思路。
- 确定递推公式
- 当word1[i - 1] 与 word2[j - 1]相同的时候
- 当word1[i - 1] 与 word2[j - 1]不相同的时候
当word1[i - 1] 与 word2[j - 1]相同的时候,dp[i][j] = dp[i - 1][j - 1];
当word1[i - 1] 与 word2[j - 1]不相同的时候,有三种情况:
情况一:删word1[i - 1],最少操作次数为dp[i - 1][j] + 1
情况二:删word2[j - 1],最少操作次数为dp[i][j - 1] + 1
情况三:同时删word1[i - 1]和word2[j - 1],操作的最少次数为dp[i - 1][j - 1] + 2
那最后当然是取最小值,所以当word1[i - 1] 与 word2[j - 1]不相同的时候,递推公式:dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
- dp数组如何初始化
从递推公式中,可以看出来,dp[i][0] 和 dp[0][j]是一定要初始化的。
dp[i][0]:word2为空字符串,以i-1为结尾的字符串word2要删除多少个元素,才能和word1相同呢,很明显dp[i][0] = i。
dp[0][j]的话同理,所以代码如下:
vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1));
for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;- 确定遍历顺序
从递推公式 dp[i][j] = min(dp[i - 1][j - 1] + 2, min(dp[i - 1][j], dp[i][j - 1]) + 1); 和dp[i][j] = dp[i - 1][j - 1]可以看出dp[i][j]都是根据左上方、正上方、正左方推出来的。
所以遍历的时候一定是从上到下,从左到右,这样保证dp[i][j]可以根据之前计算出来的数值进行计算。
- 举例推导dp数组
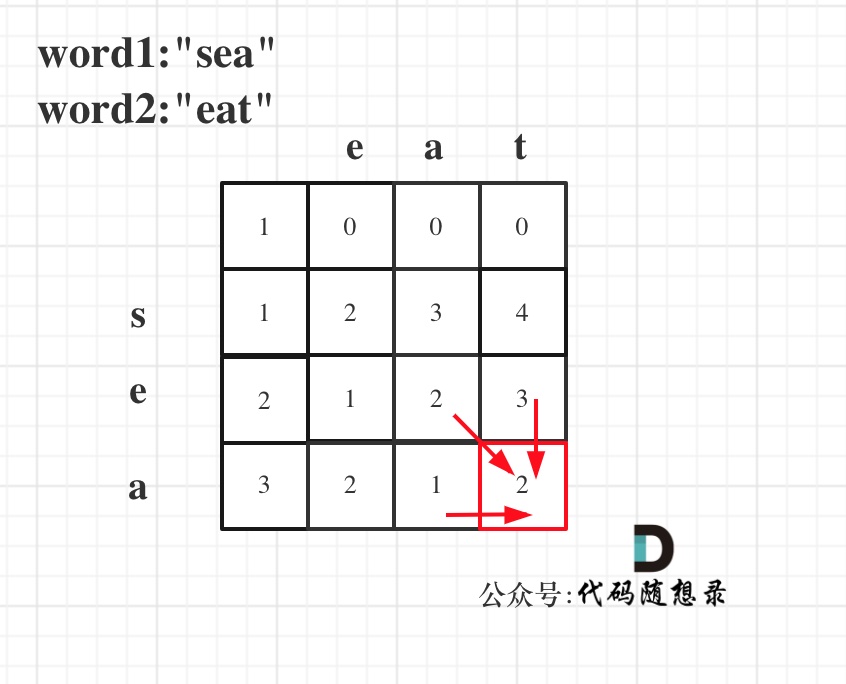
以word1:"sea",word2:"eat"为例,推导dp数组状态图如下:
以上分析完毕,代码如下:
class Solution {
public:
int minDistance(string word1, string word2) {
vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1));
for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
for (int i = 1; i <= word1.size(); i++) {
for (int j = 1; j <= word2.size(); j++) {
if (word1[i - 1] == word2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1];
} else {
dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
}
}
}
return dp[word1.size()][word2.size()];
}
};
Java:
class Solution {
public int minDistance(String word1, String word2) {
int[][] dp = new int[word1.length() + 1][word2.length() + 1];
for (int i = 0; i < word1.length() + 1; i++) dp[i][0] = i;
for (int j = 0; j < word2.length() + 1; j++) dp[0][j] = j;
for (int i = 1; i < word1.length() + 1; i++) {
for (int j = 1; j < word2.length() + 1; j++) {
if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1];
}else{
dp[i][j] = Math.min(dp[i - 1][j - 1] + 2,
Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1));
}
}
}
return dp[word1.length()][word2.length()];
}
}Python:
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
dp = [[0] * (len(word2)+1) for _ in range(len(word1)+1)]
for i in range(len(word1)+1):
dp[i][0] = i
for j in range(len(word2)+1):
dp[0][j] = j
for i in range(1, len(word1)+1):
for j in range(1, len(word2)+1):
if word1[i-1] == word2[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = min(dp[i-1][j-1] + 2, dp[i-1][j] + 1, dp[i][j-1] + 1)
return dp[-1][-1]Go: