README.md

Overview

This is a Pytorch implementation of Normalizing Flows on Tori and Spheres by Rezende et al. All 3 flows on spheres MS, EMP, and EMSRE are implemented, and the Table.1 results have been reproduced.

This is another great and helpful JAX attempt I refered though the experiment of (N=24, K=1) fails in their case.

Experiments

We conduct the experiments reported in the Table.1 in the paper, and compare results below (theirs/ours):

Quantitative

Model	KL	ESS
MS ($N_T=1,K_m=12,K_s= 32$)	0.05 / 0.03	90% / 96%
EMP ($N_T=1$)	0.50 / 0.59	43% / 42%
EMSRE ($N_T=1, K=12$)	0.82 / 0.81	42% / 48%
EMSRE ($N_T=6, K=5$)	0.19 / 0.19	75% / 82%
EMSRE ($N_T=24, K=1$)	0.10 / 0.16	85% / 84%

Qualitative

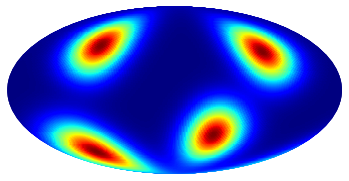
The target density is:

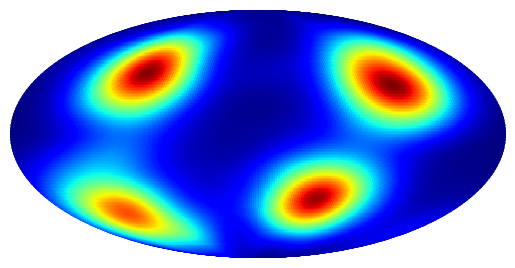
Approximated density by MS ($N_T=1,K_m=12,K_s= 32$):

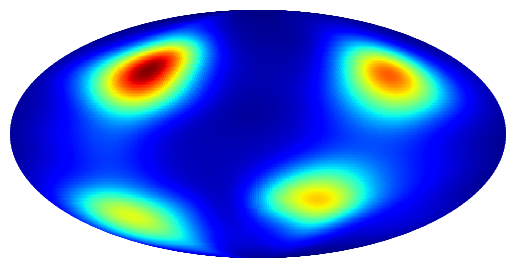
Approximated density by EMSRE ($N_T=24, K=1$):

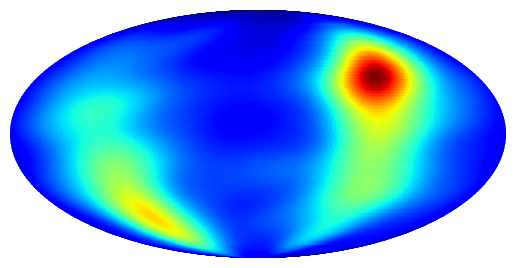
Approximated density by EMP ($N_T=1$):

Run

pip install -t requirements.txt

# run MS
python MS.py --N 1 --Km 12 --Ks 32
# run EMSRE
python EMSRE --N 24 --K 1
# run EMP
python EMP.py --N 1

Some derivations

1. The gradient of spline transforms: check the paper Neural Spline Flows

2. The gradient of mobius transforms ($\theta\rightarrow z\rightarrow h_w(z)\rightarrow \hat{\theta}$):

Note that we only want the determinant of the gradient $\partial\hat{\theta}/\partial\theta$. As the mobius transform $h$ maps a point in a circle into another point in the circle, we can have that: $$ \det|\partial\hat{\theta}/\partial\theta| =|\frac{\partial h}{\partial\theta}|_2 $$