-
Notifications
You must be signed in to change notification settings - Fork 0
/
Copy path07-anova.Rmd
120 lines (96 loc) · 5.31 KB
/
07-anova.Rmd
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
# Porovnání více průměrů
## Problém více testů
Analýza rozptylu slouží k porovnání průměrů ve více skupinách. Nabýzelo by se použít několik dvouvýběrových t-testů, ale problém s takovýmto použitím t-testů je, že chyba I. druhu v těchto testech se sčítá (viz \@ref(tests-many)). Pokud máme $k$ porovnání, pak pravděpodobnost, že uděláme chybu I. druhu je $FWER = 1-(1-\alpha)^k$. Počet porovnání $k$ můžeme vypočítat z počtu skupin $m$ jako $k = \frac{m(m-1)}{2}$. Pojďme si ukázat příklad se 4 skupinami a $\alpha=0.05$.
```{r}
m <- 4
k <- m*(m-1) / 2
alpha <- 0.05
fwer = 1-(1-alpha)^k
```
Pokud tedy máme `r m` skupiny, je celkový počet testů `r k` a pravděpodobnost chyby I. druhu `r fwer`.
## ANOVA
Řešením je tedy použít analýzu rozptylu (ANOVA). Nulová hypotéza (při 3 skupinách) tohoto testu je $H0: \mu_1=\mu_2=\mu_3$, alternativní hypotéza je $H1: \mu_i \ne \mu_j (pro\;nektere\;skupiny\;i\;a\;j)$, tedy že alespoň jeden průměr je odlišný.
Testovací statistiku $F$ vypočítáme jako $F=\frac{\frac{\sum_j^mn_j(\bar{x_j}-\bar{x})^2}{m-1}}{\frac{\sum_j^m\sum_i^n(x_{ij} - \bar{x_j})^2}{n-m}}$. Na tento výpočet se můžeme podívat také jako na podíl rozptylu uvnitř skupin / rozptylu mezi skupinami. Zároveň platí, že $\sum_j^m\sum_i^n(x_{ij} - \bar{x})^2=\sum_j^m\sum_i^n(x_{ij} - \bar{x_j})^2 + \sum_j^mn_j(\bar{x_j}-\bar{x})^2$, tedy, že celkovou sumu čtverců můžeme rozložit na sumu čtverců uvnitř skupin a na sumu čtverců mezi skupinami. Testovací statistika $F$ nabývá F rozdělení, které má 2 parametry $sv_1 = m-1$ a $sv_2=n-m$.
Pojďme si tento výpočet ukázat na simulovaných datech. Nejdříve si vytvoříme data, která budou pocházet ze 3 skupin s průměry $\mu_1=1, \mu_2=1, \mu_3=1.5$. Budeme mít 40 pozorování v každé skupině.
```{r}
set.seed(42)
mu <- c(1,1,1.5)
n <- 120 #pocet pozorování
m <- 3 # pocet skupin
# vyber
z <- rnorm(n = n, mean = mu) # nas vyber z populace
k <- rep(c(1,2,3), n/m) # vektor, ktery urcujez jake skupiny je pozorovani
```
Pojďme se podívat na průměr skupin v našem výběru.
```{r}
aggregate(z~k, FUN = mean)
```
Na zobrazení rozložení v jednotlivých skupinách použijeme boxplot. Tento graf zobrazuje, co znamenají jednotlivé hranice boxplotu.
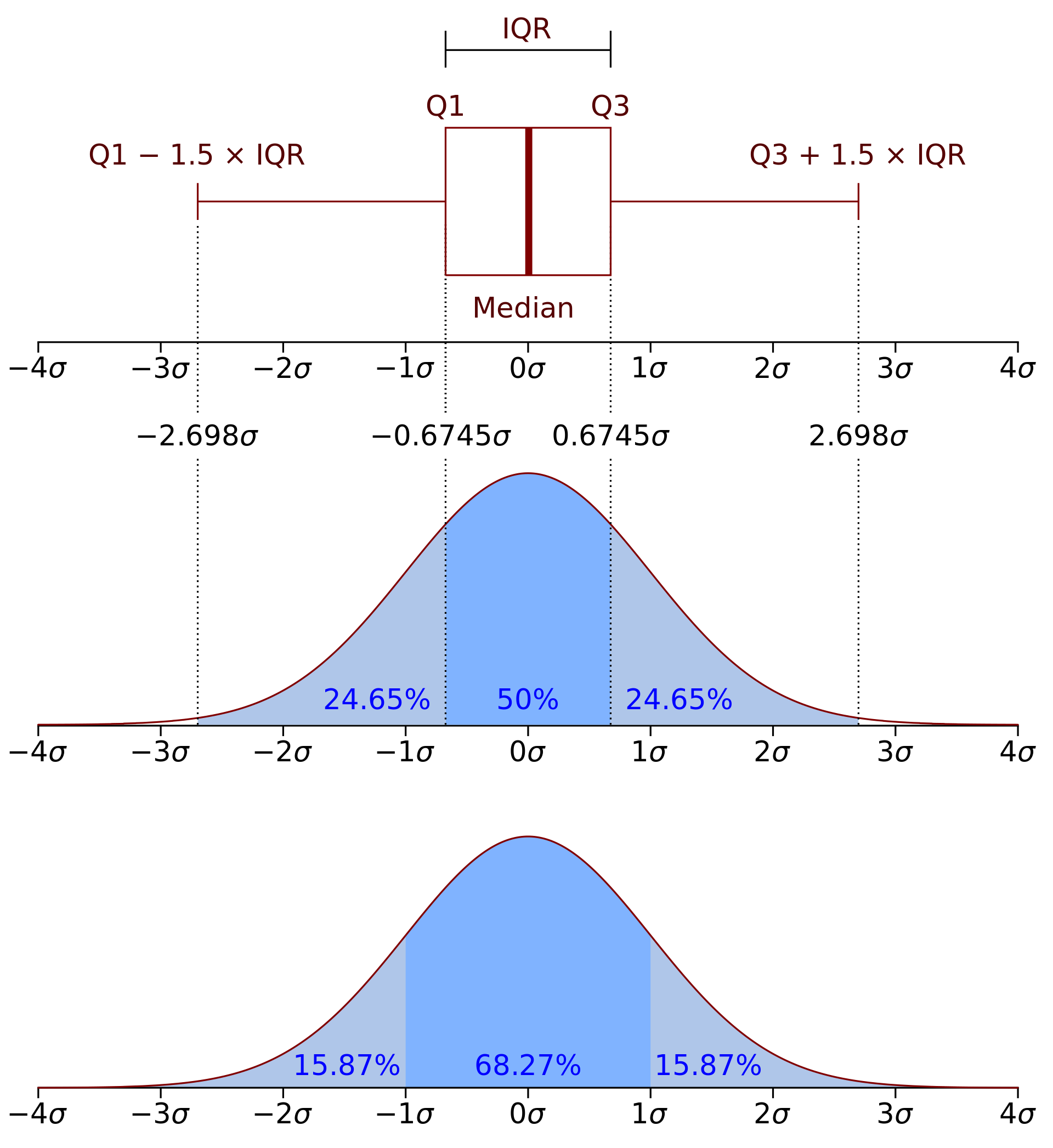
```{r, fig.cap='Rozložení závislé proměnné ve skupinách'}
boxplot(z~k,
xlab = "Skupina (nezávislá proměnná)",
ylab = "Závislá proměnná",
main = "")
```
Pro ilustraci si překryjeme boxplot jednotlivými hodnotami.
```{r, fig.cap='Rozložení závislé proměnné ve skupinách s jednotlivými pozorováními'}
boxplot(z~k,
xlab = "Skupina (nezávislá proměnná)",
ylab = "Závislá proměnná",
main = "")
points(jitter(k),z, pch = 19, col = adjustcolor("#1f77b4", alpha.f = 0.5))
```
V naší simulaci samozřejmě známe populační parametry, ale ve většině případů známe pouze výběrové hodnoty a podle nich se snažíme usoudit něco o populaci. Pojďme se tedy podívat, jaké hypotézy bychom pro tento test stanovili. $H_0$ je, že všechny 3 průměry jsou v populaci stejné a $H_1$, že alespoň jeden průměr se liší. Přistupme k výpočtu testovací staitistiky.
```{r}
sum_squares <- function(x, prumer) {
sum((x-prumer)^2)
}
ss_total <- sum_squares(z, mean(z))
ss_uvnitr <- 0
ss_mezi <- 0
for(i in 1:m) {
ss_uvnitr <- sum_squares(z[k==i], mean(z[k==i])) + ss_uvnitr
ss_mezi <- sum(k==i) * sum_squares(mean(z[k==i]), mean(z)) + ss_mezi
}
s_v_1 <- m - 1
s_v_2 <- n - m
f <- (ss_mezi / s_v_1) / (ss_uvnitr / s_v_2)
```
Celkový sum of squares je `r ss_total`, sum of squares uvnitř skupin je `r sum(ss_uvnitr)` a sum of squares mezi skupinami je `r sum(ss_mezi)`. Testovací statistika má hodnotu `r round(f, 2)`.
Přistupme k interpretaci. Vypočítejme kritickou mez pro $\alpha=0.05$ a vypočítejme hodnotu $p$. Jak vidíme, testovací statistika je v oblasti, kde zamítáme nulovou hypotézu. Tomu odpovídá také hodnota $p$, která je menší než stanovená hladina $\alpha$.
```{r, fig.cap='Rozdělení podílů rozptylu za předpokladu H0'}
alpha <- 0.05
kriticka_mez <- qf(1-alpha, df1 = s_v_1, df2 = s_v_2)
p <- 1-pf(f, df1 = s_v_1, df2 = s_v_2)
x <- seq(0, 5, length.out=1000)
pdf <- df(x, df1=s_v_1, df2=s_v_2)
plot(x, pdf,
xlab = "", ylab = "f(x)",
main = paste0("p-hodnota: ", round(p, 3), " při alpha=", alpha),
type = "l")
abline(v = kriticka_mez, col = "#1f77b4")
# oblast zamitnuti H0
lines(x[x>kriticka_mez], pdf[x>kriticka_mez],
type = "h",
col = "#1f77b4")
abline(v = f, lty = 2)
legend("topleft",
c("kritická mez", "testovací statistika"),
col = c("#1f77b4", "black"),
lty = c(1,2))
```
V `R` bychom pro tento výpočet rozkladu rozptylu použít funkci `aov`.
```{r}
m_anova <- aov(z~as.factor(k)) # pozor nezavisla promenna musi byt factor
s_anova <- summary(m_anova) # takto získáme nejzakladnejsi vysledky
print(s_anova)
```
K výpočtu statistického testu pak použijeme funkci `anova`.
```{r}
anova_vystup <- anova(m_anova)
s_v_1 <- anova_vystup$Df[1]
s_v_2 <- anova_vystup$Df[2]
f <- anova_vystup$`F value`[1]
p <- anova_vystup$`Pr(>F)`[1]
```