Generate 3D meshes based on SDFs (signed distance functions) with a dirt simple Python API.
Special thanks to Inigo Quilez for his excellent documentation on signed distance functions:
Here is a complete example that generates the model shown. This is the canonical Constructive Solid Geometry example. Note the use of operators for union, intersection, and difference.
from sdf import *
f = sphere(1) & box(1.5)
c = cylinder(0.5)
f -= c.orient(X) | c.orient(Y) | c.orient(Z)
f.save('out.stl')Yes, that's really the entire code! You can 3D print that model or use it in a 3D application.
Have a cool example? Submit a PR!
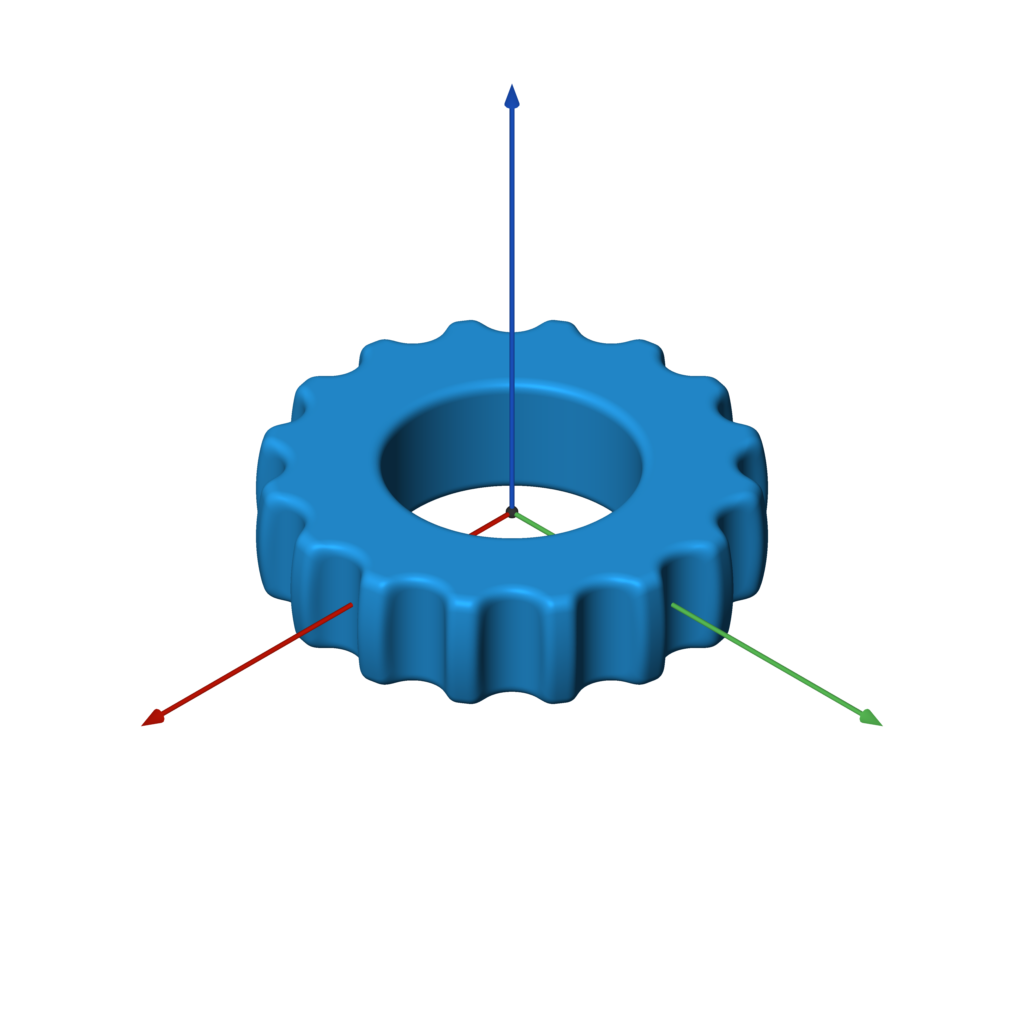
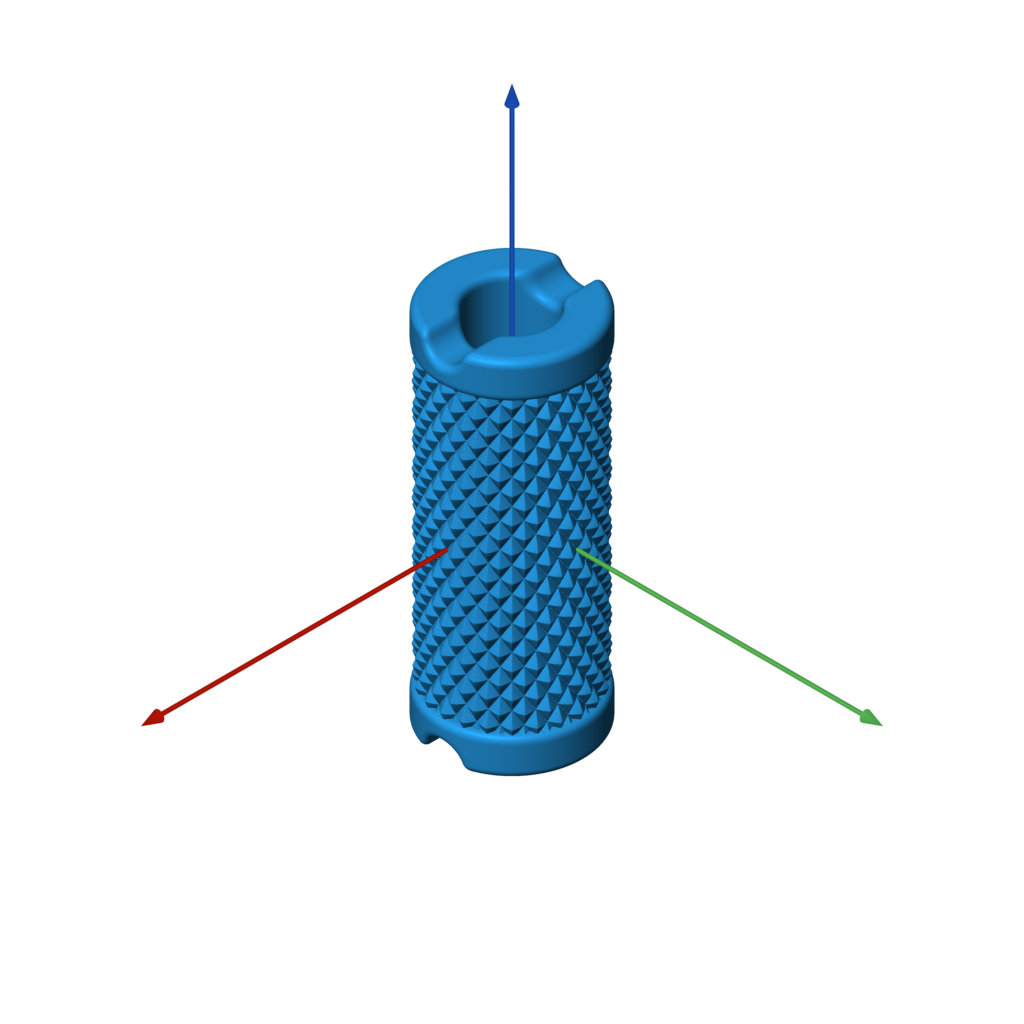
| gearlike.py | knurling.py | blobby.py | weave.py |
|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
Note that the dependencies will be automatically installed by setup.py when following the directions below.
- Python 3
- matplotlib
- meshio
- numpy
- Pillow
- scikit-image
- scipy
Use the commands below to clone the repository and install the sdf library
in a Python virtualenv.
git clone https://github.com/fogleman/sdf.git
cd sdf
virtualenv env
. env/bin/activate
pip install -e .Confirm that it works:
python examples/example.py # should generate a file named out.stlYou can skip the installation if you always run scripts that import sdf
from the root folder.
sdf natively writes binary STL files. For other formats, meshio is used (based on your output file extension). This adds support for over 20 different 3D file formats, including:
Abaqus, ANSYS msh, AVS-UCD, CGNS, DOLFIN XML, Exodus, FLAC3D, H5M, Kratos/MDPA, Medit, MED/Salome, Nastran, Neuroglancer precomputed format, Gmsh, OBJ, OFF, PERMAS, PLY, STL, Tecplot .dat, TetGen .node/.ele, SU2, UGRID, VTK, VTU, WKT (TIN), XDMF.
Find and install a 3D mesh viewer for your platform, such as MeshLab.
I have developed and use my own cross-platform mesh viewer called meshview (see screenshot). Installation is easy if you have Go and glfw installed:
$ brew install go glfw # on macOS with homebrew
$ go get -u github.com/fogleman/meshview/cmd/meshviewThen you can view any mesh from the command line with:
$ meshview your-mesh.stlSee the meshview README for more complete installation instructions.
On macOS you can just use the built-in Quick Look (press spacebar after selecting the STL file in Finder) in a pinch.
In all of the below examples, f is any 3D SDF, such as:
f = sphere()The bounding box of the SDF is automatically estimated. Inexact SDFs such as non-uniform scaling may cause issues with this process. In that case you can specify the bounds to sample manually:
f.save('out.stl', bounds=((-1, -1, -1), (1, 1, 1)))The resolution of the mesh is also computed automatically. There are two ways
to specify the resolution. You can set the resolution directly with step:
f.save('out.stl', step=0.01)
f.save('out.stl', step=(0.01, 0.02, 0.03)) # non-uniform resolutionOr you can specify approximately how many points to sample:
f.save('out.stl', samples=2**24) # sample about 16M pointsBy default, samples=2**22 is used.
Tip: Use the default resolution while developing your SDF. Then when you're done, crank up the resolution for your final output.
The SDF is sampled in batches. By default the batches have 32**3 = 32768
points each. This batch size can be overridden:
f.save('out.stl', batch_size=64) # instead of 32The code attempts to skip any batches that are far away from the surface of the mesh. Inexact SDFs such as non-uniform scaling may cause issues with this process, resulting in holes in the output mesh (where batches were skipped when they shouldn't have been). To avoid this, you can disable sparse sampling:
f.save('out.stl', sparse=False) # force all batches to be completely sampledThe SDF is sampled in batches using worker threads. By default,
multiprocessing.cpu_count() worker threads are used. This can be overridden:
f.save('out.stl', workers=1) # only use one worker threadYou can of course generate a mesh without writing it to an STL file:
points = f.generate() # takes the same optional arguments as `save`
print(len(points)) # print number of points (3x the number of triangles)
print(points[:3]) # print the vertices of the first triangleIf you want to save an STL after generate, just use:
write_binary_stl(path, points)You can plot a visualization of a 2D slice of the SDF using matplotlib. This can be useful for debugging purposes.
f.show_slice(z=0)
f.show_slice(z=0, abs=True) # show abs(f)You can specify a slice plane at any X, Y, or Z coordinate. You can also specify the bounds to plot.
Note that matplotlib is only imported if this function is called, so it
isn't strictly required as a dependency.
The code simply uses the Marching Cubes algorithm to generate a mesh from the Signed Distance Function.
This would normally be abysmally slow in Python. However, numpy is used to evaluate the SDF on entire batches of points simultaneously. Furthermore, multiple threads are used to process batches in parallel. The result is surprisingly fast (for marching cubes). Meshes of adequate detail can still be quite large in terms of number of triangles.
The core "engine" of the sdf library is very small and can be found in
mesh.py.
In short, there is nothing algorithmically revolutionary here. The goal is to provide a simple, fun, and easy-to-use API for generating 3D models in our favorite language Python.
- sdf/d2.py: 2D signed distance functions
- sdf/d3.py: 3D signed distance functions
- sdf/dn.py: Dimension-agnostic signed distance functions
- sdf/ease.py: Easing functions that operate on numpy arrays. Some SDFs take an easing function as a parameter.
- sdf/mesh.py: The core mesh-generation engine. Also includes code for estimating the bounding box of an SDF and for plotting a 2D slice of an SDF with matplotlib.
- sdf/progress.py: A console progress bar.
- sdf/stl.py: Code for writing a binary STL file.
- sdf/text.py: Generate 2D SDFs for text (which can then be extruded)
- sdf/util.py: Utility constants and functions.
It is reasonable to write your own SDFs beyond those provided by the built-in library. Browse the SDF implementations to understand how they are implemented. Here are some simple examples:
@sdf3
def sphere(radius=1, center=ORIGIN):
def f(p):
return np.linalg.norm(p - center, axis=1) - radius
return fAn SDF is simply a function that takes a numpy array of points with shape (N, 3)
for 3D SDFs or shape (N, 2) for 2D SDFs and returns the signed distance for each
of those points as an array of shape (N, 1). They are wrapped with the
@sdf3 decorator (or @sdf2 for 2D SDFs) which make boolean operators work,
add the save method, add the operators like translate, etc.
@op3
def translate(other, offset):
def f(p):
return other(p - offset)
return fAn SDF that operates on another SDF (like the above translate) should use
the @op3 decorator instead. This will register the function such that SDFs
can be chained together like:
f = sphere(1).translate((1, 2, 3))Instead of what would otherwise be required:
f = translate(sphere(1), (1, 2, 3))Remember, this is Python, so it's fully programmable. You can and should split up your model into parameterized sub-components, for example. You can use for loops and conditionals wherever applicable. The sky is the limit!
See the customizable box example for some starting ideas.
sphere(radius=1, center=ORIGIN)
f = sphere() # unit sphere
f = sphere(2) # specify radius
f = sphere(1, (1, 2, 3)) # translated spherebox(size=1, center=ORIGIN, a=None, b=None)
f = box(1) # all side lengths = 1
f = box((1, 2, 3)) # different side lengths
f = box(a=(-1, -1, -1), b=(3, 4, 5)) # specified by boundsrounded_box(size, radius)
f = rounded_box((1, 2, 3), 0.25)wireframe_box(size, thickness)
f = wireframe_box((1, 2, 3), 0.05)torus(r1, r2)
f = torus(1, 0.25)capsule(a, b, radius)
f = capsule(-Z, Z, 0.5)capped_cylinder(a, b, radius)
f = capped_cylinder(-Z, Z, 0.5)rounded_cylinder(ra, rb, h)
f = rounded_cylinder(0.5, 0.1, 2)capped_cone(a, b, ra, rb)
f = capped_cone(-Z, Z, 1, 0.5)rounded_cone(r1, r2, h)
f = rounded_cone(0.75, 0.25, 2)ellipsoid(size)
f = ellipsoid((1, 2, 3))pyramid(h)
f = pyramid(1)tetrahedron(r)
f = tetrahedron(1)octahedron(r)
f = octahedron(1)dodecahedron(r)
f = dodecahedron(1)icosahedron(r)
f = icosahedron(1)The following SDFs extend to infinity in some or all axes. They can only effectively be used in combination with other shapes, as shown in the examples below.
plane(normal=UP, point=ORIGIN)
plane is an infinite plane, with one side being positive (outside) and one side being negative (inside).
f = sphere() & plane()slab(x0=None, y0=None, z0=None, x1=None, y1=None, z1=None, k=None)
slab is useful for cutting a shape on one or more axis-aligned planes.
f = sphere() & slab(z0=-0.5, z1=0.5, x0=0)cylinder(radius)
cylinder is an infinite cylinder along the Z axis.
f = sphere() - cylinder(0.5)Yes, even text is supported!
text(name, text, width=None, height=None, texture_point_size=512)
FONT = 'Arial'
TEXT = 'Hello, world!'
w, h = measure_text(FONT, TEXT)
f = rounded_box((w + 1, h + 1, 0.2), 0.1)
f -= text(FONT, TEXT).extrude(1)Note: PIL ImageFont, which is used to load fonts, is not searching for the font by name on all operating systems.
E.g. on Ubuntu the full path to the font has to be provided. (/usr/share/fonts/truetype/freefont/FreeMono.ttf or /usr/share/fonts/truetype/roboto/unhinted/RobotoCondensed-Regular.ttf etc)
translate(other, offset)
f = sphere().translate((0, 0, 2))scale(other, factor)
Note that non-uniform scaling is an inexact SDF.
f = sphere().scale(2)
f = sphere().scale((1, 2, 3)) # non-uniform scalingrotate(other, angle, vector=Z)
f = capped_cylinder(-Z, Z, 0.5).rotate(pi / 4, X)orient(other, axis)
orient rotates the shape such that whatever was pointing in the +Z direction
is now pointing in the specified direction.
c = capped_cylinder(-Z, Z, 0.25)
f = c.orient(X) | c.orient(Y) | c.orient(Z)The following primitives a and b are used in all of the following
boolean operations.
a = box((3, 3, 0.5))
b = sphere()The named versions (union, difference, intersection) can all take
one or more SDFs as input. They all take an optional k parameter to define the amount
of smoothing to apply. When using operators (|, -, &) the smoothing can
still be applied via the .k(...) function.
f = a | b
f = union(a, b) # equivalentf = a - b
f = difference(a, b) # equivalentf = a & b
f = intersection(a, b) # equivalentf = a | b.k(0.25)
f = union(a, b, k=0.25) # equivalentf = a - b.k(0.25)
f = difference(a, b, k=0.25) # equivalentf = a & b.k(0.25)
f = intersection(a, b, k=0.25) # equivalentrepeat(other, spacing, count=None, padding=0)
repeat can repeat the underlying SDF infinitely or a finite number of times.
If finite, the number of repetitions must be odd, because the count specifies
the number of copies to make on each side of the origin. If the repeated
elements overlap or come close together, you made need to specify a padding
greater than zero to compute a correct SDF.
f = sphere().repeat(3, (1, 1, 0))circular_array(other, count, offset)
circular_array makes count copies of the underlying SDF, arranged in a
circle around the Z axis. offset specifies how far to translate the shape
in X before arraying it. The underlying SDF is only evaluated twice (instead
of count times), so this is more performant than instantiating count copies
of a shape.
f = capped_cylinder(-Z, Z, 0.5).circular_array(8, 4)blend(a, *bs, k=0.5)
f = sphere().blend(box())dilate(other, r)
f = example.dilate(0.1)erode(other, r)
f = example.erode(0.1)shell(other, thickness)
f = sphere().shell(0.05) & plane(-Z)elongate(other, size)
f = example.elongate((0.25, 0.5, 0.75))twist(other, k)
f = box().twist(pi / 2)bend(other, k)
f = box().bend(1)bend_linear(other, p0, p1, v, e=ease.linear)
f = capsule(-Z * 2, Z * 2, 0.25).bend_linear(-Z, Z, X, ease.in_out_quad)bend_radial(other, r0, r1, dz, e=ease.linear)
f = box((5, 5, 0.25)).bend_radial(1, 2, -1, ease.in_out_quad)transition_linear(f0, f1, p0=-Z, p1=Z, e=ease.linear)
f = box().transition_linear(sphere(), e=ease.in_out_quad)transition_radial(f0, f1, r0=0, r1=1, e=ease.linear)
f = box().transition_radial(sphere(), e=ease.in_out_quad)wrap_around(other, x0, x1, r=None, e=ease.linear)
FONT = 'Arial'
TEXT = ' wrap_around ' * 3
w, h = measure_text(FONT, TEXT)
f = text(FONT, TEXT).extrude(0.1).orient(Y).wrap_around(-w / 2, w / 2)extrude(other, h)
f = hexagon(1).extrude(1)extrude_to(a, b, h, e=ease.linear)
f = rectangle(2).extrude_to(circle(1), 2, ease.in_out_quad)revolve(other, offset=0)
f = hexagon(1).revolve(3)slice(other)
f = example.translate((0, 0, 0.55)).slice().extrude(0.1)



















































