Julia package for Fatou sets. Install using Pkg.add("Fatou") in Julia. See Explore Fatou sets & Fractals in Wiki for detailed examples. This package provides: fatou, juliafill, mandelbrot, newton, basin, plot, and orbit; along with various internal functionality using Reduce and Julia expressions to help compute Fatou.FilledSet efficiently. Full documentation is included. The fatou function can be applied to a Fatou.Define object to produce a Fatou.FilledSet, which can then be passed as an argument to the plot function of PyPlot. Creation of Fatou.Define objects is done via passing a parse-able function expression string (in variables z, c) and optional keyword arguments to juliafill, mandelbrot, and newton.
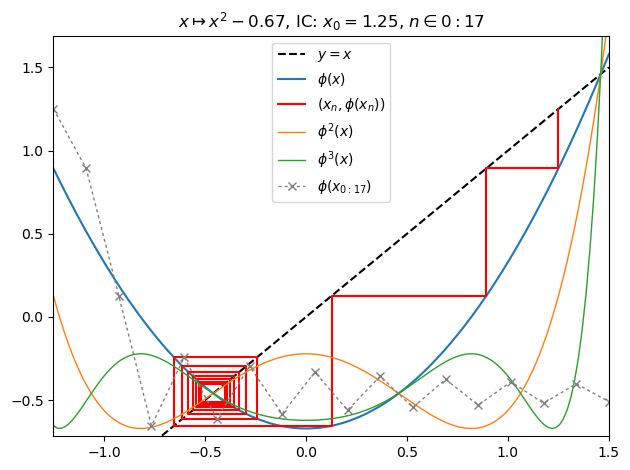
Another feature is a plot function designed to visualize real-valued-orbits. The following is a cobweb orbit plot of a function:
juliafill(:(z^2-0.67),∂=[-1.25,1.5],x0=1.25,orbit=17,depth=3,n=147) |> orbitWith fatou and plot it is simple to display a filled in Julia set:
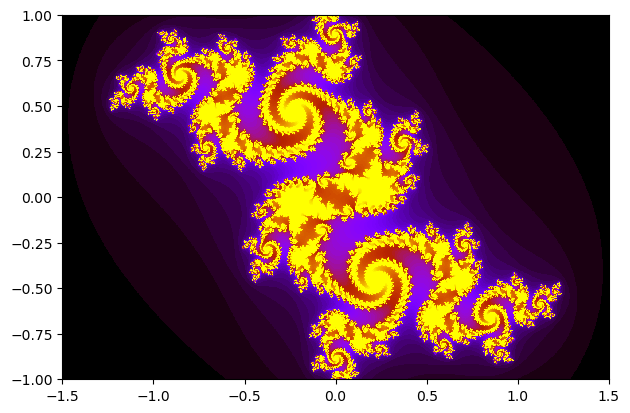
c = -0.06 + 0.67im
nf = juliafill(:(z^2+$c),∂=[-1.5,1.5,-1,1],N=80,n=1501,cmap="gnuplot",iter=true)
plot(fatou(nf), bare=true)It is also possible to switch to mandelbrot mode:
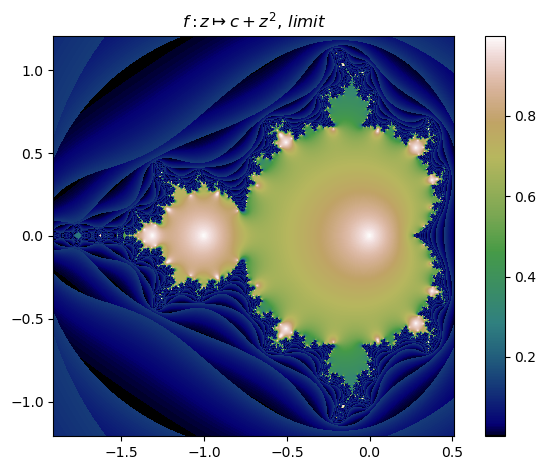
mandelbrot(:(z^2+c),n=800,N=20,∂=[-1.91,0.51,-1.21,1.21],cmap="gist_earth") |> fatou |> plotFatou also provides basin to display the the Newton / Fatou basins using set notation in LaTeX in IJulia.
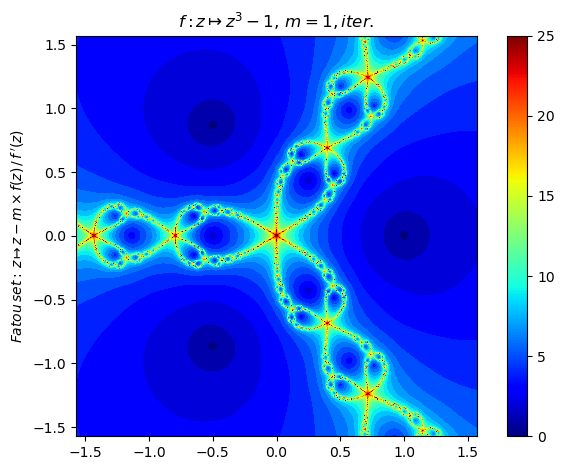
map(display,[basin(newton(:(z^3-1)),i) for i ∈ 1:3])Compute the Newton fractal Julia set for a function with annotated plot of iteration count:
nf = newton(:(z^3-1),n=800,ϵ=0.1,N=25,iter=true,cmap="jet")
nf |> fatou |> plot
basin(nf,3)Generalized Newton fractal example:
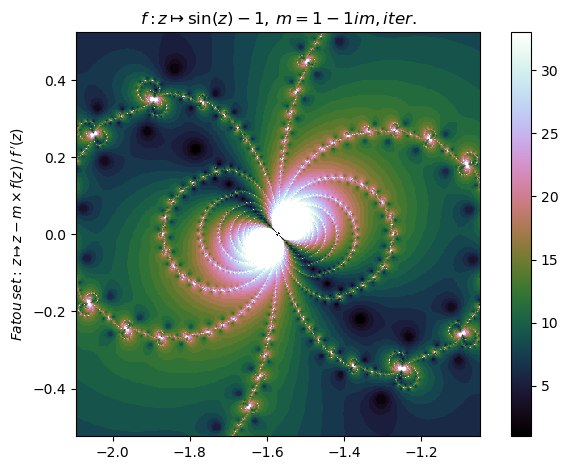
nf = newton(:(sin(z)-1),m=1-1im,∂=[-2π/3,-π/3,-π/6,π/6],n=500,N=33,iter=true,ϵ=0.05,cmap="cubehelix")
nf |> fatou |> plot
basin(nf,2)View Explore Fatou sets & Fractals in Wiki for detailed examples.