欢迎大家参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例: 输入: [1,2,3] 输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]
如果对回溯算法基础还不了解的话,我还特意录制了一期视频:带你学透回溯算法(理论篇) 可以结合题解和视频一起看,希望对大家理解回溯算法有所帮助。
此时我们已经学习了77.组合问题、 131.分割回文串和78.子集问题,接下来看一看排列问题。
相信这个排列问题就算是让你用for循环暴力把结果搜索出来,这个暴力也不是很好写。
所以正如我们在关于回溯算法,你该了解这些!所讲的为什么回溯法是暴力搜索,效率这么低,还要用它?
因为一些问题能暴力搜出来就已经很不错了!
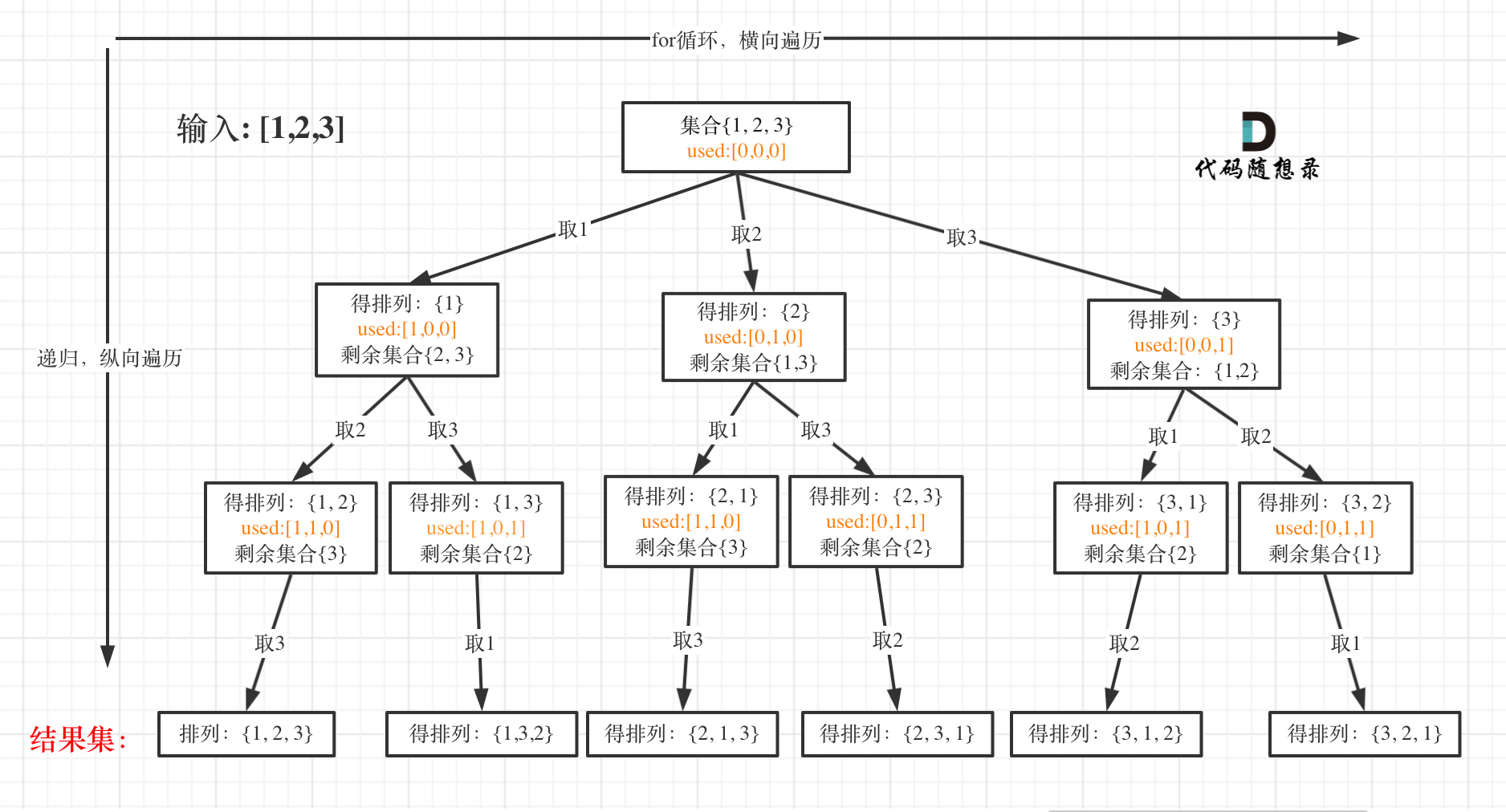
我以[1,2,3]为例,抽象成树形结构如下:
- 递归函数参数
首先排列是有序的,也就是说[1,2] 和[2,1] 是两个集合,这和之前分析的子集以及组合所不同的地方。
可以看出元素1在[1,2]中已经使用过了,但是在[2,1]中还要在使用一次1,所以处理排列问题就不用使用startIndex了。
但排列问题需要一个used数组,标记已经选择的元素,如图橘黄色部分所示:
代码如下:
vector<vector<int>> result;
vector<int> path;
void backtracking (vector<int>& nums, vector<bool>& used)
- 递归终止条件
可以看出叶子节点,就是收割结果的地方。
那么什么时候,算是到达叶子节点呢?
当收集元素的数组path的大小达到和nums数组一样大的时候,说明找到了一个全排列,也表示到达了叶子节点。
代码如下:
// 此时说明找到了一组
if (path.size() == nums.size()) {
result.push_back(path);
return;
}
- 单层搜索的逻辑
这里和77.组合问题、131.切割问题和78.子集问题最大的不同就是for循环里不用startIndex了。
因为排列问题,每次都要从头开始搜索,例如元素1在[1,2]中已经使用过了,但是在[2,1]中还要再使用一次1。
而used数组,其实就是记录此时path里都有哪些元素使用了,一个排列里一个元素只能使用一次。
代码如下:
for (int i = 0; i < nums.size(); i++) {
if (used[i] == true) continue; // path里已经收录的元素,直接跳过
used[i] = true;
path.push_back(nums[i]);
backtracking(nums, used);
path.pop_back();
used[i] = false;
}
整体C++代码如下:
class Solution {
public:
vector<vector<int>> result;
vector<int> path;
void backtracking (vector<int>& nums, vector<bool>& used) {
// 此时说明找到了一组
if (path.size() == nums.size()) {
result.push_back(path);
return;
}
for (int i = 0; i < nums.size(); i++) {
if (used[i] == true) continue; // path里已经收录的元素,直接跳过
used[i] = true;
path.push_back(nums[i]);
backtracking(nums, used);
path.pop_back();
used[i] = false;
}
}
vector<vector<int>> permute(vector<int>& nums) {
result.clear();
path.clear();
vector<bool> used(nums.size(), false);
backtracking(nums, used);
return result;
}
};大家此时可以感受出排列问题的不同:
- 每层都是从0开始搜索而不是startIndex
- 需要used数组记录path里都放了哪些元素了
排列问题是回溯算法解决的经典题目,大家可以好好体会体会。
Java:
class Solution {
List<List<Integer>> result = new ArrayList<>();// 存放符合条件结果的集合
LinkedList<Integer> path = new LinkedList<>();// 用来存放符合条件结果
boolean[] used;
public List<List<Integer>> permute(int[] nums) {
if (nums.length == 0){
return result;
}
used = new boolean[nums.length];
permuteHelper(nums);
return result;
}
private void permuteHelper(int[] nums){
if (path.size() == nums.length){
result.add(new ArrayList<>(path));
return;
}
for (int i = 0; i < nums.length; i++){
if (used[i]){
continue;
}
used[i] = true;
path.add(nums[i]);
permuteHelper(nums);
path.removeLast();
used[i] = false;
}
}
}// 解法2:通过判断path中是否存在数字,排除已经选择的数字
class Solution {
List<List<Integer>> result = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> permute(int[] nums) {
if (nums.length == 0) return result;
backtrack(nums, path);
return result;
}
public void backtrack(int[] nums, LinkedList<Integer> path) {
if (path.size() == nums.length) {
result.add(new ArrayList<>(path));
}
for (int i =0; i < nums.length; i++) {
// 如果path中已有,则跳过
if (path.contains(nums[i])) {
continue;
}
path.add(nums[i]);
backtrack(nums, path);
path.removeLast();
}
}
}Python:
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
res = [] #存放符合条件结果的集合
path = [] #用来存放符合条件的结果
used = [] #用来存放已经用过的数字
def backtrack(nums,used):
if len(path) == len(nums):
return res.append(path[:]) #此时说明找到了一组
for i in range(0,len(nums)):
if nums[i] in used:
continue #used里已经收录的元素,直接跳过
path.append(nums[i])
used.append(nums[i])
backtrack(nums,used)
used.pop()
path.pop()
backtrack(nums,used)
return resPython(优化,不用used数组):
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
res = [] #存放符合条件结果的集合
path = [] #用来存放符合条件的结果
def backtrack(nums):
if len(path) == len(nums):
return res.append(path[:]) #此时说明找到了一组
for i in range(0,len(nums)):
if nums[i] in path: #path里已经收录的元素,直接跳过
continue
path.append(nums[i])
backtrack(nums) #递归
path.pop() #回溯
backtrack(nums)
return resGo:
var res [][]int
func permute(nums []int) [][]int {
res = [][]int{}
backTrack(nums,len(nums),[]int{})
return res
}
func backTrack(nums []int,numsLen int,path []int) {
if len(nums)==0{
p:=make([]int,len(path))
copy(p,path)
res = append(res,p)
}
for i:=0;i<numsLen;i++{
cur:=nums[i]
path = append(path,cur)
nums = append(nums[:i],nums[i+1:]...)//直接使用切片
backTrack(nums,len(nums),path)
nums = append(nums[:i],append([]int{cur},nums[i:]...)...)//回溯的时候切片也要复原,元素位置不能变
path = path[:len(path)-1]
}
}Javascript:
/**
* @param {number[]} nums
* @return {number[][]}
*/
var permute = function(nums) {
const res = [], path = [];
backtracking(nums, nums.length, []);
return res;
function backtracking(n, k, used) {
if(path.length === k) {
res.push(Array.from(path));
return;
}
for (let i = 0; i < k; i++ ) {
if(used[i]) continue;
path.push(n[i]);
used[i] = true; // 同支
backtracking(n, k, used);
path.pop();
used[i] = false;
}
}
};C:
int* path;
int pathTop;
int** ans;
int ansTop;
//将used中元素都设置为0
void initialize(int* used, int usedLength) {
int i;
for(i = 0; i < usedLength; i++) {
used[i] = 0;
}
}
//将path中元素拷贝到ans中
void copy() {
int* tempPath = (int*)malloc(sizeof(int) * pathTop);
int i;
for(i = 0; i < pathTop; i++) {
tempPath[i] = path[i];
}
ans[ansTop++] = tempPath;
}
void backTracking(int* nums, int numsSize, int* used) {
//若path中元素个数等于nums元素个数,将nums放入ans中
if(pathTop == numsSize) {
copy();
return;
}
int i;
for(i = 0; i < numsSize; i++) {
//若当前下标中元素已使用过,则跳过当前元素
if(used[i])
continue;
used[i] = 1;
path[pathTop++] = nums[i];
backTracking(nums, numsSize, used);
//回溯
pathTop--;
used[i] = 0;
}
}
int** permute(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){
//初始化辅助变量
path = (int*)malloc(sizeof(int) * numsSize);
ans = (int**)malloc(sizeof(int*) * 1000);
int* used = (int*)malloc(sizeof(int) * numsSize);
//将used数组中元素都置0
initialize(used, numsSize);
ansTop = pathTop = 0;
backTracking(nums, numsSize, used);
//设置path和ans数组的长度
*returnSize = ansTop;
*returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
int i;
for(i = 0; i < ansTop; i++) {
(*returnColumnSizes)[i] = numsSize;
}
return ans;
}