Mish: Self Regularized Non-Monotonic Activation Function

Inspired by Swish Activation Function (Paper), Mish is a Self Regularized Non-Monotonic Neural Activation Function. Activation Function serves a core functionality in the training process of a Neural Network Architecture and is represented by the basic mathematical representation:

Image Credits: https://en.wikibooks.org/wiki/Artificial_Neural_Networks/Activation_Functions

An Activation Function is generally used to introduce non-linearity and over the years of theoretical machine learning research, many activation functions have been constructed with the 2 most popular amongst them being:

• ReLU (Rectified Linear Unit; f(x)=max(0,x))
  
• TanH
  

Other notable ones being:

• Softmax (Used for Multi-class Classification in the output layer)
  
• Sigmoid (f(x)=(1+e^-x)^-1;Used for Binary Classification and Logistic Regression)
  
• Leaky ReLU (f(x)=0.001x (x<0) or x (x>0))
  

Mathematics under the hood:

Mish Activation Function can be mathematically represented by the following formula:

It can also be represented by using the SoftPlus Activation Function as shown:

And it's 1^st and 2^nd derivatives are given below:

Where:

The Taylor Series Expansion of f(x) at x=0 is given by:

The Taylor Series Expansion of f(x) at x=∞ is given by:

Minimum of f(x) is observed to be ≈-0.30884 at x≈-1.1924

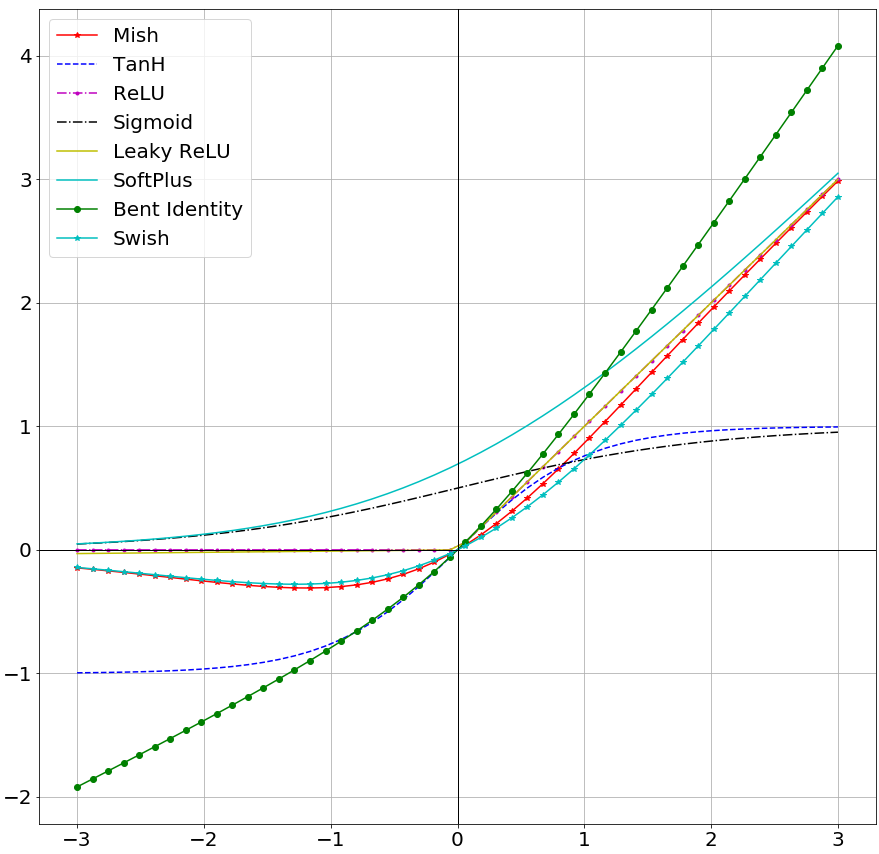
When visualized, Mish Activation Function closely resembles the function path of Swish having a small decay (preserve) in the negative side while being near linear on the positive side. It is a Monotonic Function and as observed from it's derivatives functions shown above and graph shown below, it can be noted that it has a Non-Monotonic 1^st derivative and 2^nd derivative.

Mish ranges between ≈-0.31 to ∞.

Following image shows the effect of Mish being applied on random noise (The right subplot is the Mish applied output).

Based on mathematical analysis, it is also confirmed that the function has a parametric order of continuity of: C^∞

Mish has a very sharp global minima similar to Swish, which might account to gradients updates of the model being stuck in the region of sharp decay thus may lead to bad performance levels as compared to ReLU. Mish, also being mathematically heavy, is more computationally expensive as compared to the time complexity of Swish Activation Function.

Results:

All results and comparative analysis are present in the Readme file present in the Notebooks Folder.

Summary of Results:

Comparison is done based on the high priority metric, for image classification the Top-1 Accuracy while for Generative Networks and Image Segmentation the Loss Metric. Therefore, for the latter, Mish > Baseline is indicative of better loss and vice versa.

Activation Function	Mish > Baseline Model	Mish < Baseline Model
ReLU	40	19
Swish-1	39	20
ELU(α=1.0)	4	1
Aria-2(β = 1, α=1.5)	1	0
Bent's Identity	1	0
Hard Sigmoid	1	0
Leaky ReLU(α=0.3)	2	1
PReLU(Default Parameters)	2	0
SELU	4	0
sigmoid	2	0
SoftPlus	1	0
Softsign	2	0
TanH	2	0
Thresholded ReLU(θ=1.0)	1	0

Try It!

Demo Jupyter Notebooks:

All demo jupyter notebooks are present in the Notebooks Folder.

For Source Code Implementation:

Torch:

Keras:

Tensorflow:

Conclusion:

Future Work (Coming Soon):

Support Me

Acknowledgements:

Contact:

• LinkedIn
  
• Email: [email protected]