[TOC]
- 单词向量空间与话题向量空间
- 单词向量空间
- 话题向量空间
- 潜在语义分析算法
- 矩阵奇异值分解算法
- 例子
- 非负矩阵分解算法
- 非负矩阵分解
- 潜在语义分析模型
- 非负矩阵分解的形式化
- 算法
- 潜在语义分析主要用于文本的话题分析，通过矩阵分解发现文本与单词之间的基于话题的语义关系。
- 词向量通常是稀疏的，词向量不考虑同义性，也不考虑多义性。
- 一个文本(Doc)一般有多个话题(Topic)。涉及到语义分析，要清楚什么是文本，什么是话题，什么是伪文本。
- NMF那个文章[参考文献3]发的是Nature，1999年的，不过他引不高，才9979。文章中对比了在矩阵分解框架下的VQ，PCA和NMF，说明了NMF和其他两种方法的区别。
- NMF的推导过程见参考文献4
- 潜在语义分析使用的是非概率的话题分析模型。
- 潜在语义分析是构建话题向量空间的方法(话题分析的方法)
- 单词向量转化成话题向量。文本在不同空间下的相似度用在不同空间下的向量内积表示。
- 话题向量空间$T$，单词-话题矩阵$T$，文本在话题空间的表示$Y$，话题-文本矩阵$Y$
- 本章第一个参考文献做了很多的文字说明，也有个实际的例子，可以参考下。
- 所谓表示，可以认为是在某个坐标系(空间)下的坐标。
- 非负矩阵分解旨在用较少的基向量、系数向量来表示较大的数据矩阵。
- 感觉这章的章节结构看起来不是很清晰，在内容部分重新梳理了下结构。
- 在sklearn中LSA就是截断奇异值分解，作为一种降维的手段进行处理。而NMF是单独的一个模型，都是矩阵分解的范畴。
每个向量对应一个文本，单词向量空间行对应单词，话题向量空间行对应话题。
单词-文本矩阵
$$
X=
\left[
\begin{matrix}
x_{11}&x_{12}&\cdots&x_{1n}\
x_{21}&x_{22}&\cdots&x_{2n}\
\vdots&\vdots&&\vdots\
x_{m1}&x_{m2}&\cdots&x_{mn}
\end{matrix}
\right]
$$
元素$x_{ij}$代表单词$w_i$在文本$d_j$中出现的频数或者权值。
单词多，文本少，这个矩阵是稀疏矩阵。
权值通常用TFIDF $$ TFIDF_{ij}=\frac{tf_{ij}}{tf_{\cdot j}}\log\frac{\mathrm{d}f}{\mathrm{d}f_i}\ i=1,2,\cdots,m;\ j=1,2,\cdots,n $$
一个单词在一个文本中的TFIDF是两种重要度的乘积，表示综合重要度。
每个话题由一个定义在单词集合$W$上的$m$维向量表示，称为话题向量。 $t_l=[\begin{array}&t_{1l} &t_{2l} & \cdots & t_{ml}\end{array}]^\mathrm{T}, l=1,2,\cdots,k$
这样，单词-文本矩阵$X$可以近似的表示为单词-话题矩阵$T$与话题-文本矩阵$Y$的乘积形式。这就是潜在语义分析。 $$ X\thickapprox TY $$
文本集合$D={d_1, d_2,\cdots,d_n}$ 单词集合$W={w_1,w_2,\cdots,w_m}$
表示成单词-文本矩阵$X_{m\times n}$ $$ X=\left[ \begin{matrix} &x_{11} &x_{12} &\cdots &x_{1n} \ &x_{21} &x_{22} &\cdots &x_{2n} \ &\vdots &\vdots & &\vdots\ &x_{m1} &x_{m2} &\cdots &x_{mn} \ \end{matrix} \right] $$
$$ X\thickapprox U_k\mit{\Sigma_k}V_k^\mathrm{T} \bf =\left[ \begin{matrix} u_1 &u_2 &\cdots &u_k \end{matrix} \right] \left[ \begin{matrix} \sigma_1 &0 &0 &0\ 0 &\sigma_2 &0 &0 \ 0 &0 &\ddots &0\ 0 &0 &0 &\sigma_k \end{matrix} \right] \left[ \begin{matrix} v_1^\mathrm{T}\ v_2^\mathrm{T}\ \vdots\ v_k^\mathrm{T} \end{matrix} \right] $$ 这中间$k\le n \le m$ 这里假设了文档数量要比单词数量少，其实这个假设也不一定成立。
-
$U_k$ 是$m\times k$矩阵，前$k$个相互正交的左奇异向量 -
$\mit\Sigma$ 是$k$阶方阵，前$k$个最大奇异值 -
$V_k$ 是$n\times k$矩阵，前$k$个相互正交的右奇异向量
每一列$u_l$表示一个话题，$k$个话题张成一个子空间，称为话题向量空间。 $U_k=\left[\begin{matrix}u_1&u_2&\cdots&u_k\end{matrix}\right]$
如果$u_l$表示话题向量空间，那么将文本表示成$u_l$的线性组合，就是文本在这个空间的表示。 但是，奇异值分解得到三个矩阵，最左边的是话题向量空间，那么右边的两个矩阵的乘积，则对应了话题-文本矩阵(文本的话题空间向量表示)。
这里有个点 $$ V^\mathrm{T}= \left[ \begin{matrix} v_{11}& v_{21}& \cdots& v_{n1}\ v_{12}& v_{22}& \cdots& v_{n2}\ \vdots& \vdots& & \vdots\ v_{1k}& v_{2k}& \cdots& v_{nk}\ \end{matrix} \right] $$
问题：这个矩阵是$k\times n$的，右下角标感觉应该是$v_{kn}$这种形式？ 这个矩阵是$V^\mathrm{T}$，是$k$个特征值对应的特征向量做了归一化之后的结果，参考$P_{258}$中相应的描述，$A^\mathrm{T}A$的特征向量构成正交矩阵$V$的列。$V$是右奇异向量。 这就是为什么这个矩阵下标如此表示。
$$ \begin{aligned} x_j&\thickapprox U_k(\mit\Sigma_k V_k^\mathrm{T})j\ &= \left[ \begin{matrix} u_1& u_2& \cdots& u_k \end{matrix} \right] \left[ \begin{matrix} \sigma_1v{j1}\ \sigma_2v_{j2}\ \vdots\ \sigma_kv_{jk} \end{matrix} \right] \ &=\sum_{l=1}^k\sigma_lv_{jl}u_l,j=1,2,\cdots,n \end{aligned} $$
上式是文本$d_j$的近似表达式，由$k$个话题向量$u_l$的线性组合构成。 矩阵$(\mit\Sigma_kV_k^\mathrm{T})$的每一个列向量是一个文本在话题向量空间的表示。
书中这个例子原始数据是这样的：
- The Neatest Little Guide to Stock Market Investing
- Investing For Dummies, 4th Edition
- The Little Book of Common Sense Investing: The Only Way to Guarantee Your Fair Share of Stock Market Returns
- The Little Book of Value Investing
- Value Investing: From Graham to Buffett and Beyond
- Rich Dad's Guide to Investing: What the Rich Invest in, That the Poor and the Middle Class Do Not!
- Investing in Real Estate, 5th Edition
- Stock Investing For Dummies
- Rich Dad's Advisors: The ABC's of Real Estate Investing: The Secrets of Finding Hidden Profits Most Investors Miss
去了停用词之后，做词频统计，得到了数据表。这个数据在概率潜在语义分析部分的习题中再次引用了。 对应的这部分数据，实际上还可以做一些事情。可以尝试可视化下。
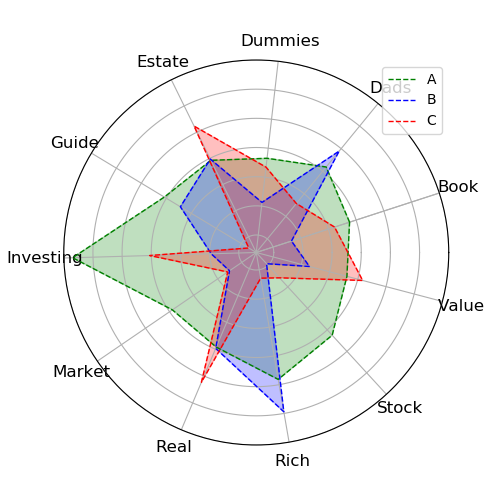上图中三个话题ABC，和不同单词的关系可以可以看出。也可以绘制单词-话题的雷达图。
这个例子里面书中给出的参考结果是按照V做了符号调整，保证V中每一行的最大值，符号为正。
其中
$W=\left[\begin{matrix}w_1& w_2& \cdots& w_k\end{matrix}\right]$表示话题向量空间
非负矩阵分解有很直观的解释，话题向量和文本向量都非负，对应着“伪概率分布”，向量的线性组合表示局部构成总体。这个其实和DL里面的意思是一样的。
可以形式化为最优化问题求解。
- 平方损失 两个非负矩阵$A=[a_{ij}]{m\times n}$和$B=[b{ij}]{m\times n}$的平方损失定义为 $$ \left|A-B\right|^2=\sum{i,j}(a_{ij}-b_{ij})^2 $$ 下界是0
- 散度
$$
D(A|B)=\sum_{i,j}\left(a_{ij}\log\frac{a_{ij}}{b_{ij}}-a_{ij}+b_{ij}\right)
$$
下界是0
$A$ 和$B$不对称。 当$\sum\limits_{i,j}a_{ij}=\sum\limits_{i,j}b_{ij}=1$时散度损失函数退化为Kullback-Leiber散度或相对熵，这时$A$和$B$是概率分布。
针对不同的损失函数有不同的问题定义
- 平方损失 $$ \min_{W,H} |X-WH|^2\ s.t. W,H\ge 0 $$
- 散度损失 $$ \min_{W,H} D(X|WH)\ s.t. W,H\ge 0 $$
这里提到目标函数只是对$W$和$H$之一的凸函数，而不是同时两个变量的凸函数，所以通过数值优化求解局部最优解。
- 平方损失 $$ H_{lj}\leftarrow H_{lj}\frac{(W^\mathrm{T}X){lj}}{(W^\mathrm{T}WH){lj}}\ W_{il}\leftarrow W_{il}\frac{(XH^\mathrm{T}){il}}{(WHH^\mathrm{T}){il}} $$
- 散度损失 $$ H_{lj}\leftarrow H_{lj}\frac{\sum\limits_i[W_{il}X_{ij}/(WH){ij}]}{\sum\limits_iW{il}}\ W_{il}\leftarrow W_{il}\frac{\sum\limits_j[H_{lj}X_{ij}/(WH){ij}]}{\sum\limits_jH{lj}} $$
- 平方损失 $$ J(W,H)=\frac{1}{2}|X-WH|^2=\frac{1}{2}\sum_{i,j}[X_{ij}-(WH){ij}]^2 $$ 采用梯度下降法求解 这里用到了矩阵求导 $$ \begin{aligned} \frac{\partial J(W,H)}{\partial W{il}}&=-\sum_j[X_{ij}-(WH){ij}]H{lj}=-[(XH^\mathrm{T}){il}-(WHH^\mathrm{T}){il}]\ \frac{\partial J(W,H)}{\partial H_{lj}}&=-[(W^\mathrm{T}X){lj}-(W^\mathrm{T}WH){lj}] \end{aligned} $$ 根据更新规则有 $$ W_{il}=W_{il}+\lambda_{il}[(XH^\mathrm{T}){il}-(WHH^\mathrm{T}){il}]\ H_{lj}=H_{lj}+\mu_{lj}[(W^\mathrm{T}X){lj}-(W^\mathrm{T}WH){lj}]\ \lambda_{il}=\frac{W_{il}}{(WHH^\mathrm{T}){il}}\ \mu{lj}=\frac{H_{lj}}{(W^\mathrm{T}WH)_{lj}} $$
输入：单词-文本矩阵$X\ge 0$，文本集合的话题个数$k$，最大迭代次数$t$； 输出：话题矩阵$W$，文本表示矩阵$H$
- 初始化
$W\ge 0$ ，并对$W$的每一列数据归一化$H\ge 0$ - 迭代 对迭代次数从$1$到$t$执行下列步骤： a. 更新$W$的元素，每次迭代对$W$的列向量归一化，使基向量为单位向量。 b. 更新$H$的元素
习题18.3