Structure and Interpretation of Computer Progams (SICP) is a classic of computer science, has been for more than two decades, and will remain so for many more. Despite it’s age, most every word in it is still as applicable today as the day it was first put to paper.
This repository includes answers to a bit more than 90% of the book’s 360-some exercises as well as material intended to help others get an idea of how to begin with the book, avoid many common pitfalls as they continue, and review interesting secondary material along the way.
It’s likely that you’ve ended up on this page precisely because you don’t need much persuading on the merits of the book, but I’ve included some famous comments on the book from internet authority figures to help seal the case:
… I bought my first copy 15 years ago, and I still don’t feel I have learned everything the book has to teach. I have learned enough to write a couple books on Lisp that (currently) have four to five stars. Yet SICP, which is pretty much the bible of our world, has only three? How can this be? Reading the reviews made it clear what happened. An optimistic professor somewhere has been feeding SICP to undergrads who are not ready for it. But it is encouraging to see how many thoughtful people have come forward to defend the book. Let’s see if we can put this in terms that the undergrads will understand – a problem set:
- Kenneth Clark said that if a lot of smart people have liked something that you don’t, you should try and figure out what they saw in it. List 10 qualities that SICP’s defenders have claimed for it.
- How is the intention of SICP different from that of Knuth? Kernighan & Ritchie? An algorithms textbook?
- Does any other book fulfill this purpose better?
- What other programming books first published in the mid 1980s are still relevant today?
- Could the concepts in this book have been presented any better in a language other than Scheme?
- Who is al? Why is his name in lowercase?
– Paul Graham
The work isn’t just admired in industry, one of the most famous computer scientists gave it high marks as well:
Those who hate SICP think it doesn’t deliver enough tips and tricks for the amount of time it takes to read. But if you’re like me, you’re not looking for one more trick, rather you’re looking for a way of synthesizing what you already know, and building a rich framework onto which you can add new learning over a career. That’s what SICP has done for me. I read a draft version of the book around 1982, when I was in grad school, and it changed the way I think about my profession. If you’re a thoughtful computer scientist (or want to be one), it will change your life too.
– Peter Norvig
A tour of some of the most interesting concepts of computing, foundations of the tools we use every day, a way to begin ”building a rich framework for which you can add new learning over a career”, a book for which ”none others fulfill it’s purpose better”, and a genuinely good time too. It’s free too!
You won’t get much out of the book if you just read it cover-to-cover however. SICP makes it your responsibility to learn what the book has to teach by doing the exercises - the true “soul” of the book.
Although the original is available online, I’d recommend you strip down to the texinfo basics or gear up to a fully-featured experience on the web.
An important first step to having fun with SICP is to have a pain free environment and REPL. I personally couldn’t imagine doing it with anything except Emacs. If you are a vim user, you can be at home in Emacs too.
With that said, the Racket community has put together something truly
astonishing with DrRacket. I have used its excellent debugger over and
over (when you want true enlightenment, debug chapter 2’s partial-tree)
and could imagine it as a great SICP environment, perhaps even surpassing
Emacs in this regard.
SICP avoids implementation-dependent behavior and, by happy coincidence, doesn’t indicate the result of functions whose behavior differs between implementations. Still, SICP is intended to be done with MIT Scheme.
Many readers have used other other Schemes, Lisps and languages pretending to be both quite successfully. I’ve seen some of the following used and have tried to approximate their fitness for the task with some features I’ve found useful:
- SICP builds an OOP system, but a proper object system is tremendously useful throughout the book.
- Function ‘redefinition’ is extremely useful required if you want to write your code in a linear fashion.
- A few subchapters of Chapter 3 require facilities for parallel computation.
- Several chapters require mutable lists. Languages like Racket do have mutable lists but use different method names and so will require you rewrite some code from the book.
- The evaluator chapters (and others), are made much easier with the introduction of tests beyond
assert.
| Language | Ease | Unit Tests | Native OOP | Function Redefinition | set! | Notes |
|---|---|---|---|---|---|---|
| Guile | 5/5 | ✓ | ✓ | ✓ | ✓ | Fully featured Lisp used by many programs like GDB as an extension language. |
| Racket | 3/5 | ✓ | ✓ | New SAT solvers and dynamic PL researchers have spawned from this schism of scheme. | ||
| MITScheme | 5/5 | ? | ✓ | ✓ | The Default SICP Choice | |
| LFErlang | 2/5 | ✓ | An ambitious competitor to Elixir by the co-creator of Erlang | |||
| Clojure | 1/5 | ✓ | ✓ | Needs no introduction |
I’ve left out two very popular choices: Common Lisp and Chicken Scheme, both I’ve heard are servicable.
The original SICP stresses the importance of Scheme’s simple syntax. Still, because of this book’s extraordinary influence, it’s been “translated” to a number of non-lisp languages including: Python, Javascript and others.
If you want to do SICP in another language it’s possible (if slightly unhinged) to do so. You will greatly suffer if your choice doesn’t support lexical closures, first-class functions and it may be the conceit of a lisp-less SICP is plainly dangerous as you will walk away with a message subtly, perhaps insidiously, different from the one the authors tried to convey.
Caveat Emptor.
SICP doesn’t rely on implementation details in MIT Scheme to communicate it’s points and translates well across implementations. Still, if this is your first time using Scheme, you might be able to benefit from a few modern implementation-specific details:
In addition to being useful for reducing redundancy and writing specialized unit-testing code, macros help cement your knowledge by forcing you to go beyond the motion of the exercises.
Be prepared to spend a few hours on this topic, syntax-rules are much
more safe & sophisticated than ‘replacement macro systems’. The most
common use-cases will be covered in your language-of-choice’s
documentation; for everything else there is Syntax Rules for the Merely
Eccentric
SICP will instruct you in building your own ‘OOP’ system and is helpful in organizing some of the more complex exercises. With that said, it’s more expedient to use your own Lisp’s object system (usually some descendent of Common Lisp’s) as well as didactic in its own right.
There’s really no conflict here. The places where SICP asks you to use its own ‘objects’ system aren’t the places you’d want to use your language’s object system. Bigger exercises (particularly those in Chapter 3) are where you benefit from a ‘proper’ object system. You could also make your own, because while it’s true that Lisp object systems can provide many features with varying degrees of adherance to the doctrine of object-orientation (whatever that implies), SICP is eased by the basics: parametricity, generic functions and/or inheritance.
There’s many ways to test Scheme code, I recommend the simplest thing
that works: SRFI-78. If you haven’t used it before, you can read some
tests for my implementation of interpreter and compiler code in test/.
SICP regularly makes reference to itself at later chapters. For example, one of the Lisp interpreter exercises in Chapter 4 makes reference to 2.71 (Chapter 2). This means that having the results of your work chronicled will make your life considerably easier.
Also, as you get deeper into the book, increasingly serious challenges will be posed. You’ll be building a Lisp interpreter, a JIT compiler, then an “actual” compiler - these are serious software engineering projects and you’ll benefit from the tools of software engineering.
SICP contains so much information that’s easy to lose track of later on if you don’t refresh your memory. A diary can also help you learn about your own learning process, serve as a reference and be personal evidence of this challenge you are about to embark on.
A variety of schemes allow you to write comments of the form: #| BLOCK COMMENT |#.
You can assign heading that you think are appropriate to each scheme file you include and
later extract those comments using a shell script.
If you’ve got experience programming in any functional programming language, this chapter will be pretty straitforward for you.
Even if you feel like the foundational material is old news to your, there are many numerical routines that you might be exposed to for the first time here.
- Foundational Scheme
- Implementing loops with recursive functions
- car/cdr/cons and other lisp list manipulation functions
- Function definition and limited explanation of “scope”
- Conditionals & predicates
- Expressions, value and defintions
- Computability and Mathematics
- Newton’s method
- Ackermann’s function
- Big O / Orders of Growth
- The Fibonacci function and various methods of implementing it
- Order of evaluation
- Monte Carlo methods for approximating PI
- Recursion
- Linear & tree recursion (along with other methods of accumulating return values)
- Euclid’s method for greatest common denominator
- A change counting “machine”
- Pascals’s Triangle
- Contrast with using function arguments or iterative solutions
- High Level Functions
- Define, convert and calculate fixed points of lots of common functions
- Use fixed points to deal with functions as proceduers
- Use `fixed-point’ function to build other, such as those that find an approximation of a continued fraction.
- Define, convert and calculate fixed points of lots of common functions
- Procedures as returned values
- Explore Newton’s method for approximating functions .
Chapter 1 often asks you to consider two implementations of a function, a “recursive” and an “iterative”, both of which call a function in their definition whose name is that function.
Some programmers are used to calling any function which calls itself “recursive”. The book directly tackles this “common misconception” in 1.2:
In contrasting iteration and recursion, we must be careful not to confuse the notion of a recursive process with the notion of a recursive procedure. When we describe a procedure as recursive, we are referring to the syntactic fact that the procedure definition refers (either directly or indirectly) to the procedure itself. But when we describe a process as following a pattern that is, say, linearly recursive, we are speaking about how the process evolves, not about the syntax of how a procedure is written. It may seem disturbing that we refer to a recursive procedure such as fact-iter as generating an iterative process. However, the process really is iterative: Its state is captured completely by its three state variables, and an interpreter need keep track of only three variables in order to execute the process.
I think it is Abelson who is the exception here, but it’s worth noting!
The trace builtin is a tool for printing the procedure call trace from within the Guile VM and is incredibly useful. Scheme implementations elsewhere have similar builtins.
↦ (pronounced “maps to”) is the mathematician’s way of writing lambda. y↦x/y
means (lambda (y) (/ x y)), that is, the function whose value at y is x/y.
This chapter is broadly concerned with the generality and principles of recursion or even more broadly with how abstract structures are built from concrete components.
This is quite a broad brush and in turn the chapter doesn’t stay put in one place for long.
- Abstractions for arithmetic
- Rationals
- Interval
- Representing lists & trees with
conscells or pointers - More advanced uses of recursion
- The 8 Queens Problem
- Permuting numbers
- Building a picture-drawing ‘language’ or library
- The mechanics of graphics
- Encoding higher order operations on graphics into lower-order actions
- Lambda calculus
- Symbolic Computation
- Computer algebra systems with automatic integration & differentiation
- Encoding, Decoding and everything in-between for Huffman Trees.
- The universality of the
(list)datastructure in Lisp - Dynamic Programming and hierarchical data structures
- Different ways to achieve language features like type-dispatch, message passing and inheritance
This book starts to give you a few nuggets of profound realization that the book is known for. It gets even better.
If you are determined to speed through SICP, I would recommend taking your time reading chapter 2.3. I, along with many others, have highlighted the the Huffman Coding material in Chapter 2.3.4.
- Symbolic Calculator by Integration & Differentiation
- Variety of binary trees and set data structures
- Huffman encoder/decoder
Although not as well known, there is a function that generates an
automatically balanced binary tree called partial-tree, and while
its inversion is apparently a requirement for getting a job at Google, the
method is also genuinely beautiful - a personal favorite of mine.
This chapter covers the tactics of abstraction. Ways to equipt ‘structure’ with operations (both of the C variety and a more abstract one) while retaining ‘genericity’.
It’s at once the least memorable and yet possibly the most important for practice of programming at large. The chapter justifies and presents simplified summaries of the implementation details of important programming language features and why they are useful.
There are only 4 exercises, so you can mostly relax and focus on the content, although both 2.73 and 2.75 show up later, so be sure you record your answers.
This chapter is the end of standard computing textbook and the beginning of SICP. If you are already a programmer, Chapter 3 presents some huge temptations to skip content, the first paragraphs of some chapters give the impression of covering what seems like already well-worn ground as a programmer - the content of the chapters differ wildly from whats “on the tin”.
Even if you are familiar, SICP has something of a reputation for taking the well-worn concepts and turning them inside out to expose their “true” structure [fn:2].
An important tip for chapter 3 is DO NOT USE A LANGUAGE WITHOUT MUTABLE LISTS:
If you are working with languages without convienent mutable data: I started out
with Racket but was forced to rewrite my work after realizing that Racket’s
mlists were not going to cut it for a chapter focused on the use and danger of
mutable structures.
Another important consideration is the parallel programming facilities of your language, the book demands a true concurrency enviroment in order for some exercises and examples to work right.
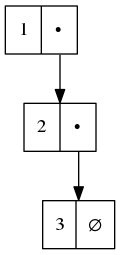
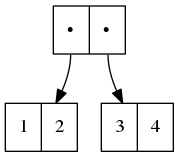
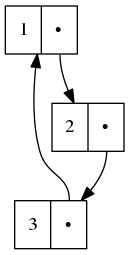
It’s often helpful to have a visual representation of what a particular list looks like, particularly once you start dealing with cycles.
The scheme script generates Graphviz diagrams which you can use to this end.
Here’s some example S-expressions with their corresponding diagram:
(define (list->graphviz lst)
"""Convert a list into a set of Graphviz instructions"""
(define number 0)
(define result "")
(define ordinals '())
(define (result-append! str)
(set! result (string-append result str)))
(define* (nodename n #:optional cell)
(format #f "cons~a~a" n (if cell (string-append ":" cell) "")))
(define* (build-connector from to #:optional from-cell)
(format #f "\t~a -> ~a;~%" (nodename from from-cell) (nodename to)))
(define (build-shape elt)
(define (build-label cell)
(cond ((null? cell) "∅") ; null character
((pair? cell) "•") ; bullet dot character
(else (format #f "~a" cell))))
(set! number (+ number 1))
(format #f "\t~a [shape=record,label=\"<car> ~a | <cdr> ~a\"];~%"
(nodename number)
(build-label (car elt))
(build-label (cdr elt))))
(define* (search xs #:optional from-id from-cell)
(let ((existing (assq xs ordinals)))
(if (pair? existing) ;; handle lists with cycles
;; we've already built a node for this entry, just make a connector
(result-append! (build-connector from-id (cdr existing) from-cell))
(begin
(result-append! (build-shape xs))
(set! ordinals (assq-set! ordinals xs number))
(let ((parent-id number))
;; make a X->Y connector
(if (number? from-id)
(result-append! (build-connector from-id parent-id from-cell)))
;; recurse
(if (pair? (car xs)) (search (car xs) parent-id "car"))
(if (pair? (cdr xs)) (search (cdr xs) parent-id "cdr")))))))
(search lst)
(string-append "digraph G {\n" result "}\n"))When list->graphviz is called, it returns a string representing the graphviz script, which you’ll
then need to feed to graphviz.
If you don’t have graphviz installed already, you can fetch it from here or with your favorite package manager:
- OSX
brew install graphviz- Redhat / Fedora
dnf install graphviz- Ubuntu
apt-get install graphviz
Once you have Graphviz installed, make a file that does (display
(list->grapviz *elt*)), where *elt* is the list you’d like to display and
feed that to dot, like so:
$ guile box_ptr.scm | dot -o /dev/stdout -Tpng > bot_pointer_diagram.png
3.34 focuses on a constraint solver. Following the books implementation is slower but does remove any function-to-function mapping confusion. On the other hand, writing your own saves you some time but requires a bit more non-SICP effort.
The book implements the primary classes of the constraint-solver as straitforward Lisp functions with closures. Classes let you solve exercises faster, write fewer lines and be more satisfied with your final result.
The following are example base-classes for the primary classes along with their
entire implementation, which allow method introduced later later in the chapter
such as process-new-value and process-forget-value to share implementation
details regardless of if they are operating on an adder or multiplier.
(define-class <constraint> ()
(lhs #:getter lhs
#:init-keyword #:lhs)
(rhs #:getter rhs
#:init-keyword #:rhs)
(total #:getter total
#:init-keyword #:total)
(operator #:getter constraint-operator)
(inverse-operator #:getter constraint-inv-operator))(define-class <connector> ()
(value #:init-value #f
#:accessor connector-value
#:setter set-connector-value)
(informant #:init-value #f
#:accessor informant
#:setter set-informant)
(constraints #:accessor constraints
#:setter set-constraints
#:init-form '()))
(define (make-connector)
(make <connector>))(define-class <probe> (<constraint>)
(name #:getter name
#:setter set-name
#:init-keyword #:name)
(connector #:getter connector
#:setter set-connector
#:init-keyword #:connector))
(define (probe name connector)
(let ((cs (make <probe> #:name name #:connector connector)))
(connect connector cs) cs))This chapter centers around the creation of a number of Scheme evaluators and is widely regarded as the most substantial chapter. The regularity with which it revises its own ideas make a testing framework and toolbelt a profitable use of your time.
If you’ve chosen a language that stresses immutability (like Racket or Clojure)
you’ll have a fair amount of extra work ahead of you - The default evaluator uses
a stack that is manipulated with the use of set!.
Don’t take my word on it though:
I’m close the finishing the last major chunk of the book. Working with two colleagues for around two hours a week, it’s taken us nearly a year to get this far. Of course, we did every exercise, and lost a lot of time trying to work around incompatibilities between standard Scheme and the interesting corners of DrScheme [now DrRacket -
mcons, I’m looking at you]. Now we use mit-scheme and I wish we had done so from the very beginning.I don’t think the book is perfect. I found the structure of Chapter 4, where a Scheme interpreter is built, confusing and irritating. The exercises are interspersed with the text in a way that doesn’t allow you to test any of your solutions unless you read ahead to get more infrastructure. This seems deeply unREPLy to me. Once I had typed in enough of the supporting code to actually run my proposed solutions, and pulled some hair out debugging my broken code, I had some marvellous moments of epiphany. That Ahah! is what maks [sic] the book’s reputation, and what makes the effort worthwhile. But it could have been better.
You’ll accomplish the following here:
- Simple Evaluator
- Implement a variable-only ’stack’ without stored function pointers.
- Implement Type-Dispatching Evaluator
- Implement all major features of scheme used thus far
- Various forms of
let letreccond- Predicates
- etc.
- Various forms of
- Simultaneous vs. Ordered
define - The Implementation of Closures
- Just-in-Time Interpreter/Compiler (the ‘analyzer’)
- Challenges of a JIT
- Lazy Evaluator
- Differences between lazy variables and a lazy interpreter
- Relationship to the promise functions
forceanddelay - Build a model of side-effects in lazy (or otherwise) evaluators
- Implementation and use of ’thunks’
- Permitting choice by adding lazy features to basic eval
- “Nondeterministic” & Logic Evaluator
- Apply our earlier DFS with backtracking knowledge to build logic solvers
- Implement a system of closures for tracking logic unification state
- Understanding rule-oriented (as opposed to procedure-oriented) computing
- Simplify problems to their essential logical form (and solve them)
- Implementation of ‘Pattern Matching’ ala Erlang
- A “true” parser
- Specify a grammar for natural language
- …and then writing something that emits all possible sentences
- Use a random evaluator to explore choices in a truly nondeterministic fashion
Some evaluator exercises occur prior to their implementation, most frequently taking the following form:
- Talk about the motivation and abstract concepts employed by an evaluator
- Discuss Implementation
- Exercises asking for implementation of various features
- Actual scheme code defining the implementation
Instead of following the book linearly, I think that having a working implementation is extremely important throughout the book, so I’d recommend you include the entire evaluator prior to completing exercises related to it. The Complete Code from SICP 2/e is available and can be used directly if you are using a mainline scheme distribution.
Starting with a testing strategy is essential to preserving sanity here; I recommend using the input → result REPL ‘dialogues’ listed in the text to ensure that you are conforming to the features that the authors expect you to use in the coming exercises.
The default Guile test runner will output a .log file to your current directory
instead of printing errors to stdout. This is an example test-runner that allows
for more immediate testing.
(use-modules (srfi srfi-64))
(define (sicp-evaluator-runner)
(let* ((runner (test-runner-null))
(num-passed 0)
(num-failed 0))
(test-runner-on-test-end! runner
(lambda (runner)
(case (test-result-kind runner)
((pass xpass) (set! num-passed (+ num-passed 1)))
((fail xfail)
(begin
(let
((rez (test-result-alist runner)))
(format #t
"~a::~a\n Expected Value: ~a | Actual Value: ~a\n Error: ~a\n Form: ~a\n"
(assoc-ref rez 'source-file)
(assoc-ref rez 'source-line)
(assoc-ref rez 'expected-value)
(assoc-ref rez 'actual-value)
(assoc-ref rez 'actual-error)
(assoc-ref rez 'source-form))
(set! num-failed (+ num-failed 1)))))
(else #t))))
(test-runner-on-final! runner
(lambda (runner)
(format #t "Passed: ~d || Failed: ~d.~%"
num-passed num-failed)))
runner))
(test-runner-factory
(lambda () (sicp-evaluator-runner)))This simple macro allows you to directly extract the expected/result pairs from the REPL excerpts.
;; Standard Evaluator Tests
(define-syntax test-eval
(syntax-rules (=> test-environment test-equal)
((test-eval expr =>)
(syntax-error "no expect statement"))
((test-eval expr => expect)
(test-eqv expect (test-evaluator 'expr test-environment)))
((test-eval expr expect)
(test-eqv expect (test-evaluator 'expr test-environment)))))Now just add tests! The next section of this guide will show you how to
automatically run tests at sensible points as part of the driver-loop.
(test-begin "Tests") ; Begin our tests
(test-begin "Evaluator") ; Begin evaluator tests
(test-begin "Basic") ; The basic (4.1) evaluator
(define test-environment (setup-environment)) ; Initialize the test environment
(define test-evaluator eval) ; Set the evaluator you wish to use
;; You can choose to use `=>' or not
(test-eval (and 1 2) => 2)
(test-eval
(let fib-iter ((a 1) (b 0) (count 4))
(if (= count 0) b
(fib-iter (+ a b) a (- count 1))))
=> 3)
;; cleanup
(set! test-environment '())
(test-end "Basic")
(test-end "Evaluator")
(test-end "Tests")Features common to
- An evaluator function driven by a switch statement
- An application function that extends the frame
- A driver loop that makes both accessible in the form of a REPL
Exercise 4.3 asks you to implement a type-dispatch scheme for the base
evaluator, allowing you to incrementally introduce functionality rather than
rewrite eval with each new feature. This turns out to be very useful
and I wrote all my evaluators in this style.
The concept is demonstrated here:
(define-class <dispatch-table> ()
(method-table #:init-value (make-hash-table)
#:getter method-table))
(define (table-ordinal op type)
(let ((opstr (symbol->string op))
(typestr (symbol->string type)))
(string-append opstr "/" typestr)))
(define-method (get (dt <dispatch-table>) op type)
(if (and (symbol? op) (symbol? type))
(hash-ref (method-table dt) (table-ordinal op type))
#f))
(define-method (put (dt <dispatch-table>) op type item)
(hash-set! (method-table dt) (table-ordinal op type) item))
(define dispatch-tt (make <dispatch-table>))
(define (install-procedure p)
"Install a procedure to the base evaluator"
(put dispatch-tt 'eval ; instead of 'eval
(car p)
(cadr p))
...
(install-procedure `(and ,eval-and))
(install-procedure `(let* ,(λ (exp env) (zeval (let*->nested-lets exp) env))))
(install-procedure `(undefine ,eval-undefinition))
(install-procedure `(while ,(λ (exp env) (zeval (make-while exp) env))))Just as you dispatched a procedure specific to an evaluator above, you can do
the same with the driver-loop implementation provided to each evaluator.
- You’ll want to be able to quickly switch the evaluator invoked by
driver-loopas you progress through the chapter and later chapters have a radically different loop. - Geiser is a very popular scheme integration module for Emacs Lisp that you will probably use. Like many IDE-integrated IDE’s it doesn’t deal well with a program that requests user input on
stdin. - You can share more code, even between radically different implementations.
My approach is simple - add an entry to a table of driver-loop implementations
which are chosen at runtime.
;; This function is what actually gets called to invoke your evaluator's REPL
(define (driver-loop evaluator)
((get dispatch-tt 'driver-loop evaluator)))
(define (install-driver-loop evaluator fn)
"Install a new `driver-loop' REPL"
(put dispatch-tt 'driver-loop evaluator fn))
; base evaluator implementation from 4.14
(define (base-driver-loop)
(prompt-for-input ";;; Base(zeval) input:")
(let ((input (read)))
(let ((output
(zeval input
the-global-environment)))
(announce-output output-prompt)
(user-print output)))
(base-driver-loop))
;; install the base driver loop
(install-driver-loop 'eval base-driver-loop)
(define inside-repl?
"A method to determine if we are inside a REPL or being executed directly"
(eq? #f (assq-ref (current-source-location) 'filename)))
...
;; at the end of the file, you can specify which loop you want to invoke when
;; you run.
(if inside-repl? 'ready ;; we want the repl available ASAP if were inside emacs
(begin
;; load our tests
(load "test/evaluator.scm")
;; start the REPL
(driver-loop 'amb)))
;;; EOFMany code excerpts from the text cannot be directly used in the evaluator
provided by the book itself. Before you initialize your evaluators environment,
be sure to add the following to your primitive-procedures
(append! primitive-procedures
`((+ ,+) (- ,-) (* ,*) (/ ,/) (abs ,abs)
(= ,=) (< ,<) (<= ,<=) (> ,>) (> ,>=)
(not ,not)
(list ,list)
(member ,member)
(display ,display)))Additionally, let is missing from the `amb` interpreter as well. Just add the
one used by the analyze evaluator.
The `amb` evaluator presented in 4.3 is far from simple and requires patience and an eye for detail to work out whats really going on.
The query evaluator may be the most difficult material yet, particularly if you aren’t previously familiar with a language like Prolog.
This material requires very careful reading to grasp its operation and the book frequently spends more time on its consequences over its content.
If you want to grasp its implementation, you will have to read and reread chapter 4.4.4.
The unification step, which the book itself describes as the most unintuitive aspect, should be read thoroughly: It’s the material that actually does the process of generating deductions from premises.
It’s also important to remember that much of the rest of the material is devoted to various ‘optimizations’ and implementation details that can easily derail you.
The query evaluator presented as is cannot compute rules of the form (?x rule
?y) as many questions ask to, simply translate them to the postfix form and you
will be fine.
(rule (?x next-to ?y in (?x ?y . ?u)))
⇩
(rule (next-to ?x ?y in (?x ?y . ?u)))
Chapter 5 begins with modeling a ‘register machine’, approximate to many contemporary architectures. Asking you to implement (or invent) a register machine language, complete with the control flow constructs and data structures needed.
This is where the chapter is known for ‘going off the deep end’: building a scheme compiler with tail call optimization, garbage collection, lexical addressing, tracing and so on.
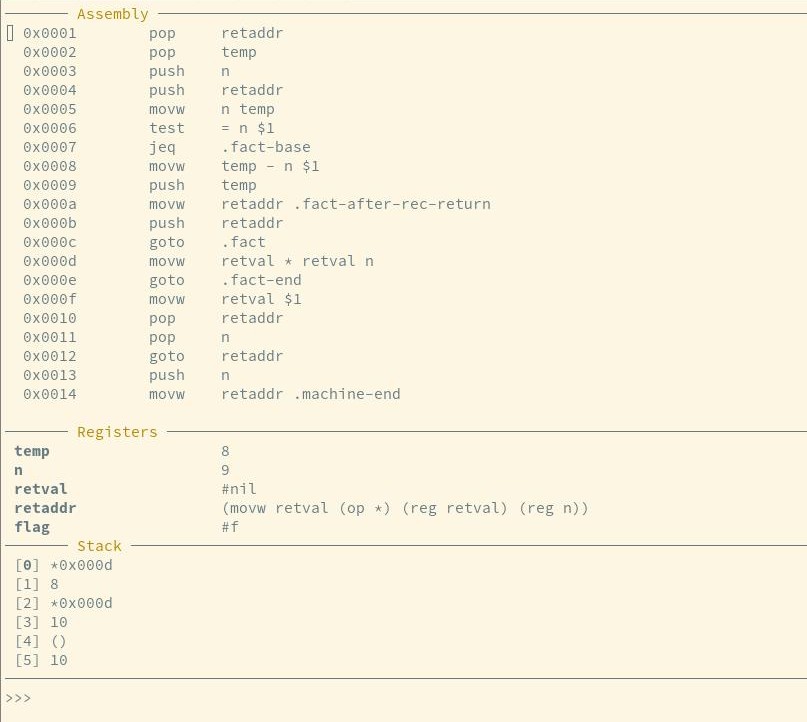
I’ve built a REPL debugger for the Ch5 machine language. This can be used with whichever assembly variant you decide to write your exercises in, but if are familiar with x86 assembly, I think it will seem like a little slice of home.
If you’d like to use it, you can find its source code in machine/gui.scm.
Here is a macro and runner function for generating a quick register machine definition as follows:
(define-register-machine newtons
#:registers (x guess)
#:ops ((good-enough ,newton/good-enough?)
(improve ,newton/improve))
#:assembly ((assign guess (const 1.0))
improve
(test (op good-enough) (reg guess) (reg x))
(branch (label end-newton))
(assign guess (op improve) (reg guess) (reg x))
(goto (label improve))
end-newton))(define (machine-run mach init)
"Run a machine with the registers initialized to the alist in `init' and
then dumps the values of all registers"
(map (λ (el) (set-register-contents! mach (car el) (cdr el))) init)
(start mach)
(map
(λ (reg) (cons (car reg)
(get-contents (get-register mach (car reg)))))
(mach 'dump-registers)))
(define-syntax define-register-machine
(syntax-rules ()
((define-register-machine var #:registers registers #:ops ops #:assembly assembly)
(define var (build-rmachine
#:registers 'registers
#:ops `ops
#:assembly 'assembly)))))Everyone has regrets, let’s hope you have fewer by reading mine.
So many books have irrelevant exercises, SICP doesnt. I sped through the end of SICP Chapter 3 - I won’t do it again.
Implementingor, and and other other connective logical statements in the
amb evaluator would really be neat – I just installed a primitive procedure.
Donald Knuth wrote a whole fasc. of TAOCP on permutation problems and I can see why. I’ve come up with no less than 2 dozen ways reformulations do them over the years: including counting in base-N (where N is the number of permuted items), the traditional map-n-slap, round-robin (what is called “bell method”)
I always feel guilty not giving an honest effort before looking up an algorithm online and I always feel somewhat stumped on permutation problems. Sure, I know the “classic” swap algorithm, I’ve (obviously) implemented the method for permuting a list in Chapter 2, but something essential feels like it’s getting left out.
Take Exercise 4.39, which (loosely) is to solve the floor puzzle without using
amb AND take advantage of knowledge about the puzzle to make it perform
better than ‘depth first’.
I ended up looking at someone elses solution here - This one is hard to solve without resorting “tricks”, such as applying eliminative logic beforehand to solve the problem. This mixes all sorts of different kinds of representations of data and many solutions are incorrect.
I completed the exercises but I started to get to a really uncomfortable point, especially in Exercise 4.49 that this was some deep metaphor for parsing fully-specified grammars.
This is a list of exercises I haven’t completed for some reason or another.
- 4.32
- 4.33
- 4.34
- 4.44
- 4.47 (started to get unbelievably bored of these exercises)
- 4.48 (started to get unbelievably bored of these exercises)
- 4.49 (started to get unbelievably bored of these exercises)
- 4.69 (This is both tricky and somewhat irrelevant)
- 4.71
- 4.74
[fn:1] Including all exercises asking you to draw with pen and paper as well as those specified above. [fn:2] Ever wonder how people make calculators and webservers using ONLY type-inference without ANY instructions specified? Turns out thats actually fairly simple and you are just going to have to read the whole thing to find ou.