https://leetcode.com/problems/path-sum-ii/description/
Given a binary tree and a sum, find all root-to-leaf paths where each path's sum equals the given sum.
Note: A leaf is a node with no children.
Example:
Given the below binary tree and sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ / \
7 2 5 1
Return:
[
[5,4,11,2],
[5,8,4,5]
]
这道题目是求集合,并不是求值,而是枚举所有可能,因此动态规划不是特别切合,因此我们需要考虑别的方法。
这种题目其实有一个通用的解法,就是回溯法。 网上也有大神给出了这种回溯法解题的 通用写法,这里的所有的解法使用通用方法解答。 除了这道题目还有很多其他题目可以用这种通用解法,具体的题目见后方相关题目部分。
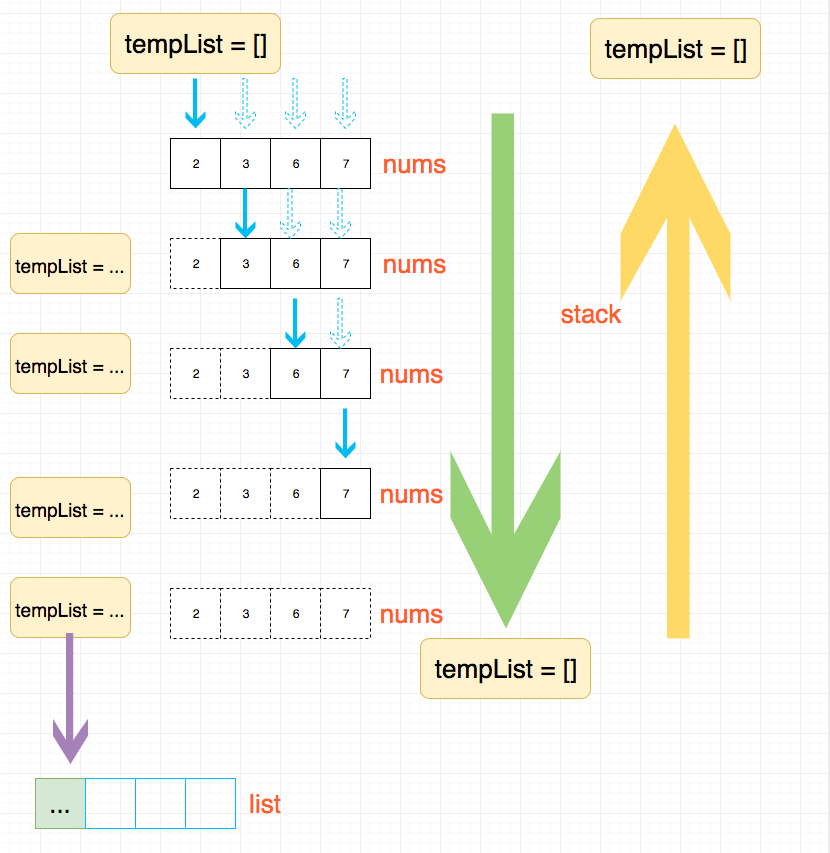
我们先来看下通用解法的解题思路,我画了一张图:
通用写法的具体代码见下方代码区。
- 回溯法
- backtrack 解题公式
- 语言支持:JS,C++
JavaScript Code:
/*
* @lc app=leetcode id=113 lang=javascript
*
* [113] Path Sum II
*/
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
function backtrack(root, sum, res, tempList) {
if (root === null) return;
if (root.left === null && root.right === null && sum === root.val)
return res.push([...tempList, root.val]);
tempList.push(root.val);
backtrack(root.left, sum - root.val, res, tempList);
backtrack(root.right, sum - root.val, res, tempList);
tempList.pop();
}
/**
* @param {TreeNode} root
* @param {number} sum
* @return {number[][]}
*/
var pathSum = function(root, sum) {
if (root === null) return [];
const res = [];
backtrack(root, sum, res, []);
return res;
};C++ Code:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<vector<int>> pathSum(TreeNode* root, int sum) {
auto ret = vector<vector<int>>();
auto temp = vector<int>();
backtrack(root, sum, ret, temp);
return ret;
}
private:
void backtrack(const TreeNode* root, int sum, vector<vector<int>>& ret, vector<int>& tempList) {
if (root == nullptr) return;
tempList.push_back(root->val);
if (root->val == sum && root->left == nullptr && root->right == nullptr) {
ret.push_back(tempList);
} else {
backtrack(root->left, sum - root->val, ret, tempList);
backtrack(root->right, sum - root->val, ret, tempList);
}
tempList.pop_back();
}
};