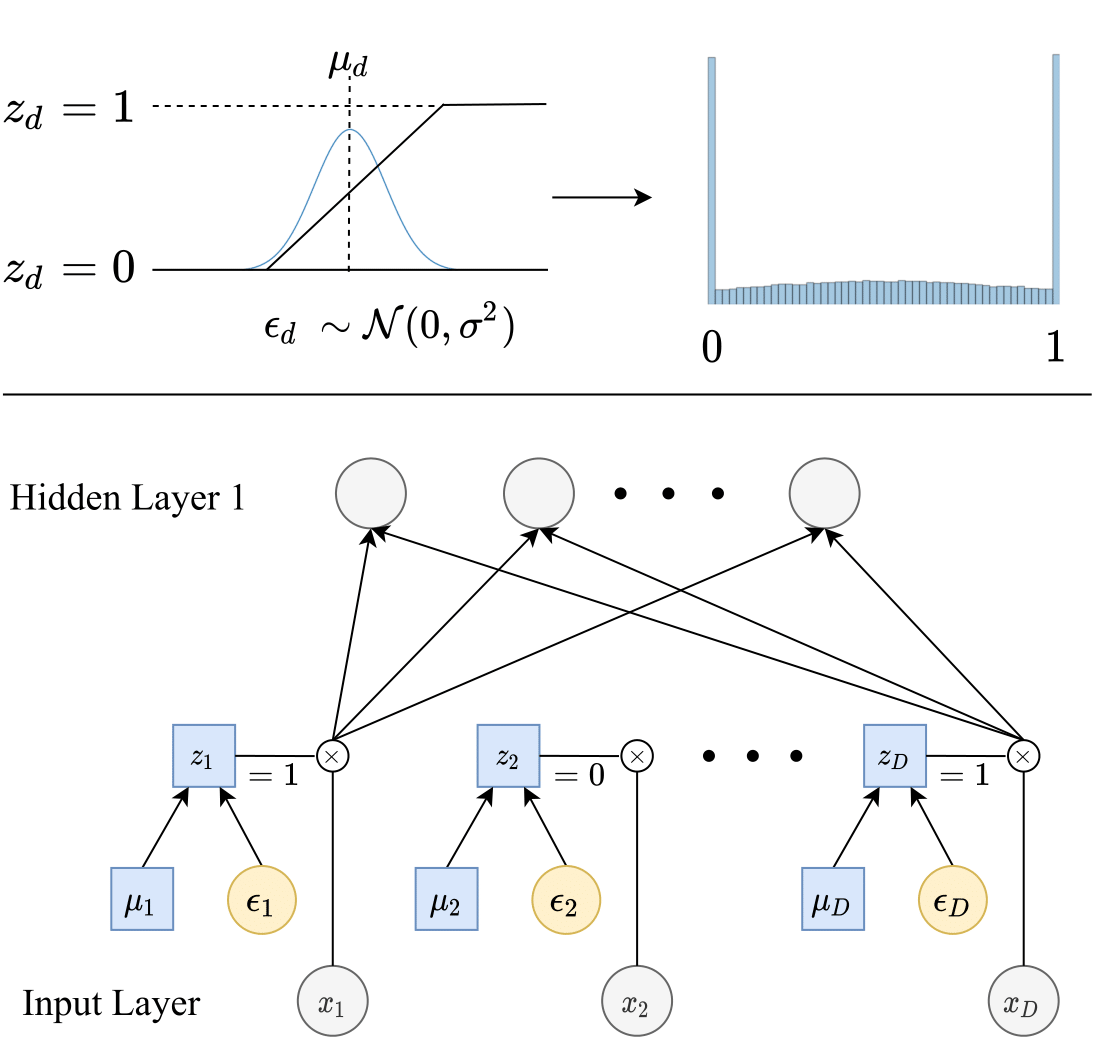
Feature Selection using Stochastic Gates (STG) is a method for feature selection in neural network estimation problems. The new procedure is based on probabilistic relaxation of the l0 norm of features, or the count of the number of selected features. The proposed framework simultaneously learns either a nonlinear regression or classification function while selecting a small subset of features.
To install with pip, run the following command:
pip install --user stg
You can also clone the repository and install manually:
git clone
cd stg/python
python setup.py install --user
Once you install the library, you can import STG to create a model instance:
from stg import STG
model = STG(task_type='regression',input_dim=X_train.shape[1], output_dim=1, hidden_dims=[500, 50, 10], activation='tanh', optimizer='SGD', learning_rate=0.1, batch_size=X_train.shape[0], feature_selection=True, sigma=0.5, lam=0.1, random_state=1, device="cpu")
model.fit(X_train, y_train, nr_epochs=3000, valid_X=X_valid, valid_y=y_valid, print_interval=1000)
# Start training...
For more details, please see our Colab notebooks:
You first need to install the python package.
Run the following command in your R console:
install.packages("Rstg")
git clone git://github.com/runopti/stg.git
cd stg/python
python setup.py install --user
cd ../Rstg
R CMD INSTALL .
Please set the python path for reticulate to the python environment that you install the python stg package via this command in your R console or at the beginning of your R script.
reticulate::use_python("path_to_your_python_env_with_stg")
Then you can instantiate a trainer:
stg_trainer <- stg(task_type='regression', input_dim=100L, output_dim=1L, hidden_dims = c(500,50, 10), activation='tanh', optimizer='SGD', learning_rate=0.1, batch_size=100L, feature_selection=TRUE, sigma=0.5, lam=0.1, random_state=0.1)
You can then fit the model to data as follows:
# After preparing `X_train`, `y_train`, `X_valid`, and `y_valid'
stg_trainer$fit(X_train, y_train, nr_epochs=5000L, valid_X=X_valid, valid_y=y_valid, print_interval=1000L)
You can save your trained model
stg_trainer$save_checkpoint('r_test_model.pth')
and load the model
stg_trainer$load_checkpoint('r_test_mode.pth')
We thank Junchen Yang for his help to develop the R wrapper. Some of our codebase and its structure is inspired by https://github.com/vacancy/Jacinle.
If you find our library useful in your research, please consider citing us:
@incollection{icml2020_5085,
author = {Yamada, Yutaro and Lindenbaum, Ofir and Negahban, Sahand and Kluger, Yuval},
booktitle = {Proceedings of Machine Learning and Systems 2020},
pages = {8952--8963},
title = {Feature Selection using Stochastic Gates},
year = {2020}
}