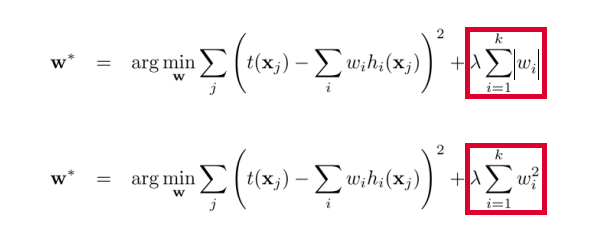A feature engineering kit for each issue, to give you a deeper and deeper understanding of the work of feature engineering!
专项突破,每一期都会分享一些很实用的特征工程技巧,从理论到实践,循序渐进,目前本项目已累计撰写了28期内容,为了方便统一阅读,📦打包成了一份PDF供朋友们下载。 欢迎关注微信公众号《SAMshare》,与作者阿Sam取得交流!
随着我们在机器学习、数据建模、数据挖掘分析这条发展路上越走越远,其实越会感觉到特征工程的重要性,平时我们在很多地方都会看到一些很好的特征工程技巧,本项目的目的就是把这些小技巧打包成一个又一个的小锦囊,供大家去阅读。
首先是当前更新到的目录,方便大家去查找内容!
数据集大家可以点击这里去进行下载哈😆
- Tip1:特征无量纲化的常见操作方法
- Tip2:怎么进行多项式or对数的数据变换
- Tip3:常用的统计图在Python里怎么画?
- Tip4:怎么去除DataFrame里的缺失值?
- Tip5:怎么把被错误填充的缺失值还原?
- Tip6:怎么定义一个方法去填充分类变量的空值?
- Tip7:怎么定义一个方法去填充数值变量的空值?
- Tip8:怎么把几个图表一起在同一张图上显示?
- Tip9:怎么把画出堆积图来看占比关系?
- Tip10:怎么对满足某种条件的变量修改其变量值?
- Tip11:怎么通过正则提取字符串里的指定内容?
- Tip12:如何利用字典批量修改变量值?
- Tip13:如何对类别变量进行独热编码?
- Tip14:如何把“年龄”字段按照我们的阈值分段?
- Tip15:如何使用sklearn的多项式来衍生更多的变量?
- Tip16:如何根据变量相关性画出热力图?
- Tip17:如何把分布修正为类正态分布?
- Tip18:怎么找出数据集中有数据倾斜的特征?
- Tip19:怎么尽可能地修正数据倾斜的特征?
- Tip20:怎么简单使用PCA来划分数据且可视化呢?
- Tip21:怎么简单使用LDA来划分数据且可视化呢?
- Tip22:怎么来管理我们的建模项目文件?
- Tip23:怎么批量把特征中的离群点给安排一下?
- Tip24:彻底了解一下WOE和IV
- Tip25:一文介绍特征工程里的卡方分箱,附代码实现
- Tip26:今天一起搞懂机器学习里的L1与L2正则化
- Tip27:金融风控里的WOE前的分箱一定要单调吗?
- Tip28:如何在Python中处理不平衡数据
第一招,从简单的特征量纲处理开始,这里介绍了3种无量纲化操作的方法,同时也附上相关的包以及调用方法,欢迎补充!
无量纲化:即nondimensionalize 或者dimensionless,是指通过一个合适的变量替代,将一个涉及物理量的方程的部分或全部的单位移除,以求简化实验或者计算的目的。——百度百科
进行进一步解释,比如有两个字段,一个是车行走的公里数,另一个是人跑步的距离,他们之间的单位其实差异还是挺大的,其实两者之间无法进行比较的,但是我们可以进行去量纲,把他们的变量值进行缩放,都统一到某一个区间内,比如0-1,便于不同单位或者量级之间的指标可以进行比较or加权!
下面的是sklearn里的一些无量纲化的常见操作方法。
from sklearn.datasets import load_iris
#导入IRIS数据集
iris = load_iris()
#标准化,返回值为标准化后的数据
from sklearn.preprocessing import StandardScaler
StandardScaler().fit_transform(iris.data)
#区间缩放,返回值为缩放到[0, 1]区间的数据
from sklearn.preprocessing import MinMaxScaler
MinMaxScaler().fit_transform(iris.data)
#归一化,返回值为归一化后的数据
from sklearn.preprocessing import Normalizer
Normalizer().fit_transform(iris.data)数据变换,这个操作在特征工程中用得还是蛮多的,一个特征在当前的分布下无法有明显的区分度,但一个小小的变换则可以带来意想不到的效果,而这个小小的变换,也就是今天给大家分享的小锦囊。
按照指定的degree,进行多项式操作从而衍生出新变量(当然这是针对每一列特征内的操作)。
举个栗子:
from sklearn.datasets import load_iris
#导入IRIS数据集
iris = load_iris()
iris.data[0]
# Output: array([ 5.1, 3.5, 1.4, 0.2])tt = PolynomialFeatures().fit_transform(iris.data)
tt[0]
# Output: array([ 1. , 5.1 , 3.5 , 1.4 , 0.2 , 26.01, 17.85, 7.14, 1.02, 12.25, 4.9 , 0.7 , 1.96, 0.28, 0.04])因为PolynomialFeatures()方法默认degree是2,所以只会进行二项式的衍生。
一般来说,多项式变换都是按照下面的方式来的:
f = kx + b 一次函数(degree为1)
f = ax^2 + b*x + w 二次函数(degree为2)
f = ax^3 + bx^2 + c*x + w 三次函数(degree为3)
这类的转换可以适当地提升模型的拟合能力,对于在线性回归模型上的应用较为广泛。
这个操作就是直接进行一个对数转换,改变原先的数据分布,而可以达到的作用主要有:
1)取完对数之后可以缩小数据的绝对数值,方便计算;
2)取完对数之后可以把乘法计算转换为加法计算;
3)还有就是分布改变带来的意想不到的效果。
numpy库里就有好几类对数转换的方法,可以通过from numpy import xxx 进行导入使用。
log:计算自然对数
log10:底为10的log
log2:底为2的log
log1p:底为e的log
from sklearn.datasets import load_iris
#导入IRIS数据集
iris = load_iris()
#多项式转换
#参数degree为度,默认值为2
from sklearn.preprocessing import PolynomialFeatures
PolynomialFeatures().fit_transform(iris.data)
#对数变换
from numpy import log1p
from sklearn.preprocessing import FunctionTransformer
#自定义转换函数为对数函数的数据变换
#第一个参数是单变元函数
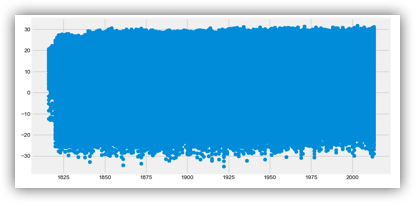
FunctionTransformer(log1p).fit_transform(iris.data) 这里的话我们介绍几种很简单但也很实用的统计图绘制方法,分别有条形图、饼图、箱体图、直方图以及散点图,关于这几种图形的含义这边就不多做解释了。
今天用到两个数据集,数据集大家可以在公众号回复"特征工程"来获取,分别是Salary_Ranges_by_Job_Classification和GlobalLandTemperaturesByCity。
# 导入一些常用包
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
plt.style.use('fivethirtyeight')
#解决中文显示问题,Mac
%matplotlib inline
from matplotlib.font_manager import FontProperties
# 引入第 1 个数据集 Salary_Ranges_by_Job_Classification
salary_ranges = pd.read_csv('./data/Salary_Ranges_by_Job_Classification.csv')
# 引入第 2 个数据集 GlobalLandTemperaturesByCity
climate = pd.read_csv('./data/GlobalLandTemperaturesByCity.csv')
# 移除缺失值
climate.dropna(axis=0, inplace=True)
# 只看中国
# 日期转换, 将dt 转换为日期,取年份, 注意map的用法
climate['dt'] = pd.to_datetime(climate['dt'])
climate['year'] = climate['dt'].map(lambda value: value.year)
climate_sub_china = climate.loc[climate['Country'] == 'China']
climate_sub_china['Century'] = climate_sub_china['year'].map(lambda x:int(x/100 +1))
# 设置显示的尺寸
plt.rcParams['figure.figsize'] = (4.0, 4.0) # 设置figure_size尺寸
plt.rcParams['image.interpolation'] = 'nearest' # 设置 interpolation style
plt.rcParams['image.cmap'] = 'gray' # 设置 颜色 style
plt.rcParams['savefig.dpi'] = 100 #图片像素
plt.rcParams['figure.dpi'] = 100 #分辨率
plt.rcParams['font.family'] = ['Arial Unicode MS'] #正常显示中文
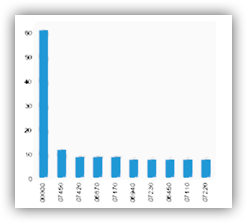
# 绘制条形图
salary_ranges['Grade'].value_counts().sort_values(ascending=False).head(10).plot(kind='bar')
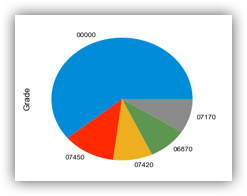
# 绘制饼图
salary_ranges['Grade'].value_counts().sort_values(ascending=False).head(5).plot(kind='pie')
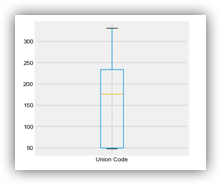
# 绘制箱体图
salary_ranges['Union Code'].value_counts().sort_values(ascending=False).head(5).plot(kind='box')
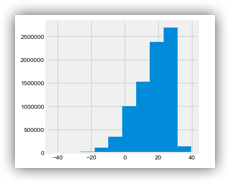
# 绘制直方图
climate['AverageTemperature'].hist()
# 绘制散点图
x = climate_sub_china['year']
y = climate_sub_china['AverageTemperature']
fig, ax = plt.subplots(figsize=(10,5))
ax.scatter(x, y)
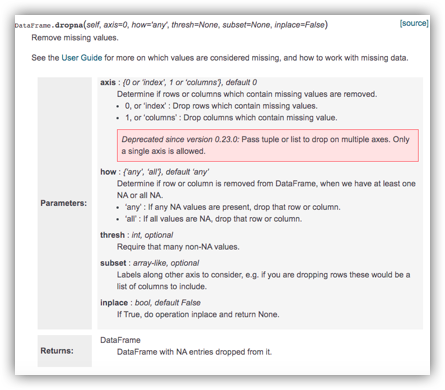
plt.show()这个我们经常会用,当我们发现某个变量的缺失率太高的时候,我们会直接对其进行删除操作,又或者说某一行我不想要了,想单独删除这一行数据,这个我们该怎么处理呢?这里介绍一个方法,DataFrame.dropna(),具体可以看下图:
从方法介绍可以看出,我们可以指定 axis 的值,如果是0,那就是按照行去进行空值删除,如果是1则是按照列去进行操作,默认是0。
同时,还有一个参数是how ,就是选择删除的条件,如果是 any则是如果存在一个空值,则这行(列)的数据都会被删除,如果是 all的话,只有当这行(列)全部的变量值为空才会被删除,默认的话都是any 。
好了,举几个栗子,我们还是用climate数据集:
# 引入数据集
import pandas as pd
climate = pd.read_csv('./data/GlobalLandTemperaturesByCity.csv')
# 保留一部分列
data = climate.loc[:,['dt','AverageTemperature','AverageTemperatureUncertainty','City']]
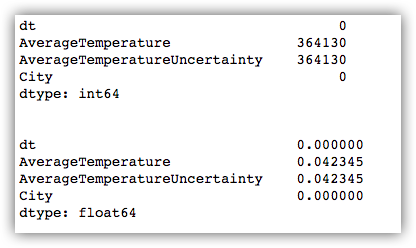
data.head()# 查看有多少缺失值
print(data.isnull().sum())
print('\n')
# 查看缺失值占比
print(data.isnull().sum()/len(data))# 原始模样
print(data.head())
print('\n')
# 默认参数axis=0,根据索引(index)删除指定的行,删除第0行数据
print(data.drop(0).head())
print('\n')
# axis=1,根据列名(columns)删除指定的列,删除'dt'列
print(data.drop('dt',axis=1).head())
print('\n')
# 移除含有缺失值的行,直接结果作为新df
data.dropna(axis=0, inplace=True)上个小锦囊讲到我们可以对缺失值进行丢弃处理,但是这种操作往往会丢失了很多信息的,很多时候我们都需要先看看缺失的原因,如果有些缺失是正常存在的,我们就不需要进行丢弃,保留着对我们的模型其实帮助会更大的。
此外,还有一种情况就是我们直接进行统计,它是没有缺失的,但是实际上是缺失的,什么意思?就是说缺失被人为(系统)地进行了填充,比如我们常见的用0、-9、-999、blank等来进行填充缺失,若真遇见这种情况,我们可以这么处理呢?
很简单,那就是还原缺失!
# 引入数据集(皮马印第安人糖尿病预测数据集)
pima_columns = ['times_pregment','plasma_glucose_concentration','diastolic_blood_pressure','triceps_thickness',
'serum_insulin','bmi','pedigree_function','age','onset_disbetes']
pima = pd.read_csv('./data/pima.data', names=pima_columns)
# 处理被错误填充的缺失值0,还原为 空(单独处理)
pima['serum_insulin'] = pima['serum_insulin'].map(lambda x:x if x !=0 else None)
# 检查变量缺失情况
pima['serum_insulin'].isnull().sum()
# Output:374# 批量操作 还原缺失值
columns = ['serum_insulin','bmi','plasma_glucose_concentration','diastolic_blood_pressure','triceps_thickness']
for col in columns:
pima[col].replace([0], [None], inplace=True)
# 检查变量缺失情况
pima.isnull().sum()之前我们说过如何删除掉缺失的行,但是如何我们需要的是填充呢?比如说用众数来填充缺失,或者用某个特定值来填充缺失值?这个也是我们需要掌握的特征工程的方法之一,对于用特定值填充缺失,其实比较简单了,我们可以直接用fillna() 方法就可以,下面我来讲一个通用的办法,除了用特定值填充,我们还可以自定义,比如说用”众数“来填充等等。
这里我们用到了TransformerMixin方法,然后自定义一个填充器来进行缺失值的填充。
这里我们造一个数据集来测试我们的代码:
# 本次案例使用的数据集
import pandas as pd
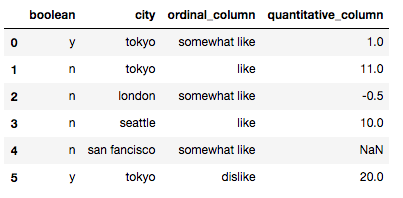
X = pd.DataFrame({'city':['tokyo',None,'london','seattle','san fancisco','tokyo'],
'boolean':['y','n',None,'n','n','y'],
'ordinal_column':['somewhat like','like','somewhat like','like','somewhat like','dislike'],
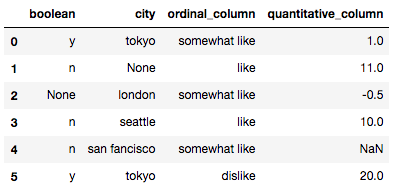
'quantitative_column':[1,11,-.5,10,None,20]})
X可以看出,这个数据集有三个分类变量,分别是boolean、city和ordinal_column,而这里面有两个字段存在空值。
# 填充分类变量(基于TransformerMixin的自定义填充器,用众数填充)
from sklearn.base import TransformerMixin
class CustomCategoryzImputer(TransformerMixin):
def __init__(self, cols=None):
self.cols = cols
def transform(self, df):
X = df.copy()
for col in self.cols:
X[col].fillna(X[col].value_counts().index[0], inplace=True)
return X
def fit(self, *_):
return self
# 调用自定义的填充器
cci = CustomCategoryzImputer(cols=['city','boolean'])
cci.fit_transform(X)这个锦囊和上一个差不多了,不过这个换一个方法 Imputer 。
同样的,我们还是造一个数据集:
# 本次案例使用的数据集
import pandas as pd
X = pd.DataFrame({'city':['tokyo',None,'london','seattle','san fancisco','tokyo'],
'boolean':['y','n',None,'n','n','y'],
'ordinal_column':['somewhat like','like','somewhat like','like','somewhat like','dislike'],
'quantitative_column':[1,11,-.5,10,None,20]})
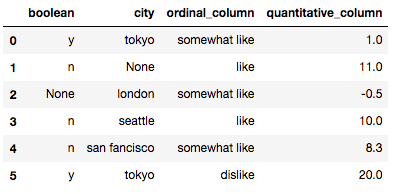
X可以看出,这个数据集有一个数值变量quantitative_columns,存在一行缺失值,我们直接调用sklearn的preprocessing方法里的Imputer。
# 填充数值变量(基于Imputer的自定义填充器,用众数填充)
from sklearn.preprocessing import Imputer
class CustomQuantitativeImputer(TransformerMixin):
def __init__(self, cols=None, strategy='mean'):
self.cols = cols
self.strategy = strategy
def transform(self, df):
X = df.copy()
impute = Imputer(strategy=self.strategy)
for col in self.cols:
X[col] = impute.fit_transform(X[[col]])
return X
def fit(self, *_):
return self
# 调用自定义的填充器
cqi = CustomQuantitativeImputer(cols = ['quantitative_column'], strategy='mean')
cqi.fit_transform(X)未来几个特征锦囊的内容会使用泰坦尼克号的数据集,大家可以在下面的链接去下载数据哈。
Titanic数据集下载:https://www.kaggle.com/c/titanic/data
首先我们要知道,做特征工程之前知道数据的分布和关联情况是极为重要的,因此把这些信息做一些可视化的操作是很重要的操作和技能,今天我们就来学习下怎么画很多张图,然后可以一并显示在同一张上吧,专业来说就是画子图。
# 导入相关库
import pandas as pd
import numpy as np
from pandas import Series,DataFrame
# 导入泰坦尼的数据集
data_train = pd.read_csv("./data/titanic/Train.csv")
data_train.head()import matplotlib.pyplot as plt
# 设置figure_size尺寸
plt.rcParams['figure.figsize'] = (8.0, 6.0)
fig = plt.figure()
# 设定图表颜色
fig.set(alpha=0.2)
# 第一张小图
plt.subplot2grid((2,3),(0,0))
data_train['Survived'].value_counts().plot(kind='bar')
plt.ylabel(u"人数")
plt.title(u"船员获救情况 (1为获救)")
# 第二张小图
plt.subplot2grid((2,3),(0,1))
data_train['Pclass'].value_counts().plot(kind="bar")
plt.ylabel(u"人数")
plt.title(u"乘客等级分布")
# 第三张小图
plt.subplot2grid((2,3),(0,2))
plt.scatter(data_train['Survived'], data_train['Age'])
plt.ylabel(u"年龄")
plt.grid(b=True, which='major', axis='y')
plt.title(u"按年龄看获救分布 (1为获救)")
# 第四张小图,分布图
plt.subplot2grid((2,3),(1,0), colspan=2)
data_train.Age[data_train.Pclass == 1].plot(kind='kde')
data_train.Age[data_train.Pclass == 2].plot(kind='kde')
data_train.Age[data_train.Pclass == 3].plot(kind='kde')
plt.xlabel(u"年龄")
plt.ylabel(u"密度")
plt.title(u"各等级的乘客年龄分布")
plt.legend((u'头等舱', u'2等舱',u'3等舱'),loc='best')
# 第五张小图
plt.subplot2grid((2,3),(1,2))
data_train.Embarked.value_counts().plot(kind='bar')
plt.title(u"各登船口岸上船人数")
plt.ylabel(u"人数")
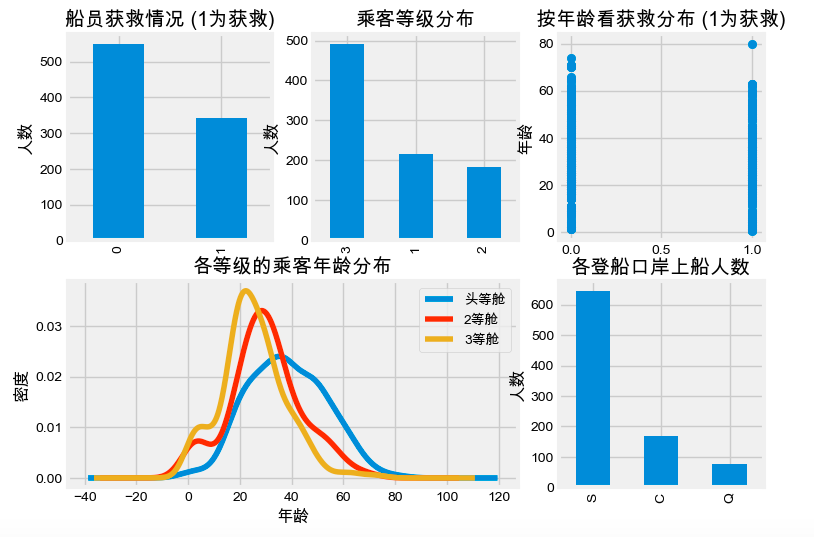
plt.show()我们从上面的可视化操作结果可以看出,其实可以看出一些规律,比如说生还的几率比死亡的要大,然后获救的人在年龄上区别不大,然后就是有钱人(坐头等舱的)的年龄会偏大等。
未来几个特征锦囊的内容会使用泰坦尼克号的数据集,大家可以在下面的链接去下载数据哈。
Titanic数据集下载:https://www.kaggle.com/c/titanic/data
上次的锦囊我知道了怎么把几张图放在一张图上去显示,但是这个只是一种排版方式的操作,今天分享一个画堆积图的方法,可以用来看类别占比关系,有助于我们去了解数据,发现数据里的规律。
# 导入相关库
import pandas as pd
import numpy as np
from pandas import Series,DataFrame
# 导入泰坦尼的数据集
data_train = pd.read_csv("./data/titanic/Train.csv")
data_train.head()# 设置figure_size尺寸
plt.rcParams['figure.figsize'] = (5.0, 4.0)
#看看各乘客等级的获救情况
fig = plt.figure()
fig.set(alpha=0.8)
Survived_0 = data_train.Pclass[data_train.Survived == 0].value_counts()
Survived_1 = data_train.Pclass[data_train.Survived == 1].value_counts()
df=pd.DataFrame({u'获救':Survived_1, u'未获救':Survived_0})
df.plot(kind='bar', stacked=True)
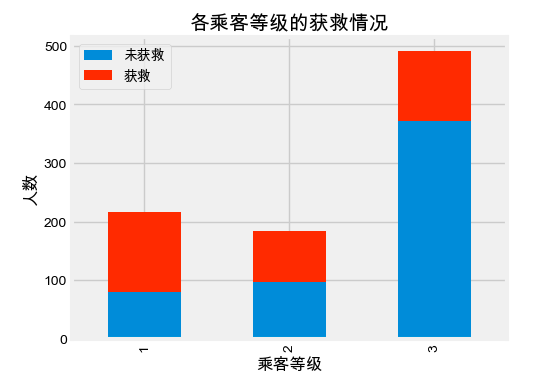
plt.title(u"各乘客等级的获救情况")
plt.xlabel(u"乘客等级")
plt.ylabel(u"人数")
plt.show()未来几个特征锦囊的内容会使用泰坦尼克号的数据集,大家可以在下面的链接去下载数据哈。
Titanic数据集下载:
https://www.kaggle.com/c/titanic/data
这里我们使用loc函数,这个方式实在是太好用了!
首先我们先理解一下这个loc应该怎么用吧,然后再举几个实战例子来理解一下。
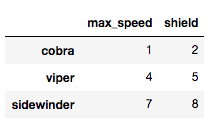
我们要知道loc函数的意思就是通过行标签索引行数据,最直接的就是看看文档,引用文档里的数据集:
df = pd.DataFrame([[1, 2], [4, 5], [7, 8]],index=['cobra', 'viper', 'sidewinder'],columns=['max_speed', 'shield'])
df下面的小例子就是从文档里拿过来的,很全面的示例了一些应用操作。
那么通过上面的学习,你大概也知道了loc的简单用法了,下面就介绍下在特征工程里我们清洗某些数据时候,可以通过这函数来修改变量值,从而达到我们的某些目的。
下面我们还是用泰坦尼号的数据集:
# 导入相关库
import pandas as pd
import numpy as np
from pandas import Series,DataFrame
# 导入泰坦尼的数据集
data_train = pd.read_csv("./data/titanic/Train.csv")
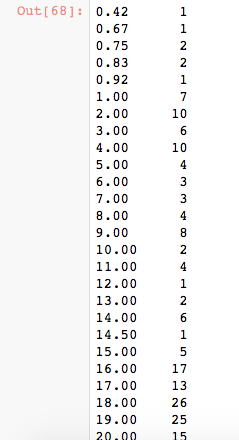
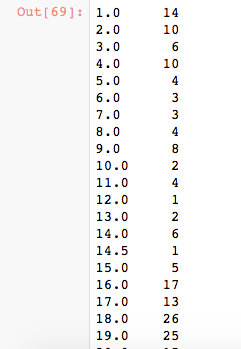
data_train['Age'].value_counts().sort_index()我们可以看出有些年龄有小于1岁的,比如0.42、0.67之类的,我们这里就使用一下loc来把这些小于1岁的修改为1岁吧,如果没有意外,应该岁数为1的统计数会变为14个。
data_train.loc[(data_train.Age<=1),'Age'] = 1
data_train['Age'].value_counts().sort_index()这个正则表达式在我们做字符提取中是十分常用的,先前有一篇文章有介绍到怎么去使用正则表达式来实现我们的目的,大家可以先回顾下这篇文章。
我们还是用一下泰坦尼克号的数据集,大家可以在下面的链接去下载数据哈。
Titanic数据集下载:
https://www.kaggle.com/c/titanic/data
# 导入相关库
import pandas as pd
import numpy as np
from pandas import Series,DataFrame
import re
# 导入泰坦尼的数据集
data_train = pd.read_csv("./data/titanic/Train.csv")
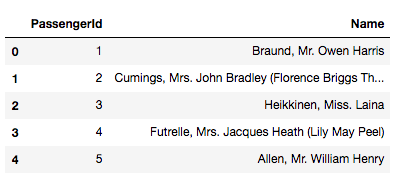
data_train.head()我们现在可以提取下这name里的称谓,比如Mr、Miss之类的,作为一个新列,代码如下:
data['Title'] = data['Name'].map(lambda x: re.compile(", (.*?)\.").findall(x)[0])
data.head()我们之前看这代码其实有点懵的,不过这是因为大家可能对正则表达式的规则不太熟悉,所以下面有几个相关的可以参考下。
import re
str = 'xxdaxxabxxacabxxcdabddbxxssbdffbggxx'
# 一个'.'就是匹配\n(换行符)以外的任何字符
print(re.findall(r'a.b',str))
# 一个'*'前面的字符出现0次或以上
print(re.findall(r'a*b',str))
# 匹配从.*前面的字符为起点,到后面字符为终点的所有内容,直到返回所有
print(re.findall(r'xx.*xx',str))
# 非贪婪,和上面的一样,不过是用过一次就不会再用,,以列表的形式返回
print(re.findall(r'xx.*?xx',str))
# 非贪婪,与上面是一样的,只是与上面相比,多了一个括号,只保留括号中的内容
print(re.findall(r'xx(.*?)xx',str))
# 保留a,b中间的内容
print(re.findall(r'xx(.+?)xx',str))
print(re.findall(r'xx(.+?)xx',str)[0])所以,看了这些后,应该就可以理解上面的pattern的含义了!
这里我们假设有这么一种情况,一个字段里的变量值,需要把某几个变量值修改为同一个值,然后其他几个变量值修改为另外一个,那么我们有什么简单的办法可以完成呢?这边,我推荐一个字典映射的办法!
我们还是用一下泰坦尼克号的数据集,大家可以在下面的链接去下载数据哈。
Titanic数据集下载:
https://www.kaggle.com/c/titanic/data
# 导入相关库
import pandas as pd
import numpy as np
from pandas import Series,DataFrame
import re
# 导入泰坦尼的数据集
data_train = pd.read_csv("./data/titanic/Train.csv")
# 提取其中几列
data = data_train.loc[:,['PassengerId','Name']]
# 提取称谓
data['Title'] = data['Name'].map(lambda x: re.compile(", (.*?)\.").findall(x)[0])
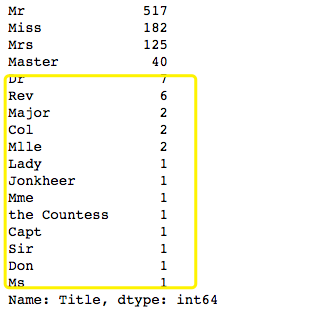
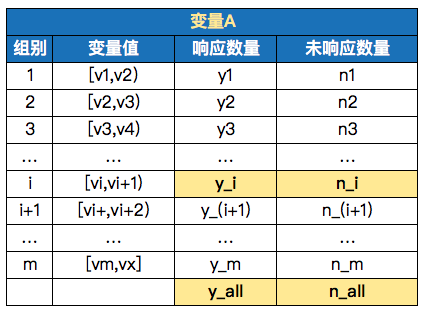
data.Title.value_counts()就好像我刚刚所说的,需要把黄色框框里的变量值修改掉,而且是按照我们的想法,比如capt和Dr合为一体,统一叫officer。
# 定义一个空字典来收集映射关系
title_Dict = {}
title_Dict.update(dict.fromkeys(['Capt', 'Col', 'Major', 'Dr', 'Rev'], 'Officer'))
title_Dict.update(dict.fromkeys(['Don', 'Sir', 'the Countess', 'Dona', 'Lady'], 'Royalty'))
title_Dict.update(dict.fromkeys(['Mme', 'Ms', 'Mrs'], 'Mrs'))
title_Dict.update(dict.fromkeys(['Mlle', 'Miss'], 'Miss'))
title_Dict.update(dict.fromkeys(['Mr'], 'Mr'))
title_Dict.update(dict.fromkeys(['Master','Jonkheer'], 'Master'))
title_Dict我们把映射关系用字典来存储,到时候直接可以拿来用。
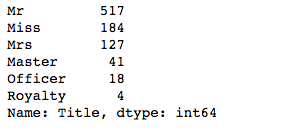
data['Title'] = data['Title'].map(title_Dict)
data.Title.value_counts()很多时候我们需要对类别变量进行独热编码,然后才可以作为入参给模型使用,独热的方式有很多种,这里介绍一个常用的方法 get_dummies吧,这个方法可以让类别变量按照枚举值生成N个(N为枚举值数量)新字段,都是0-1的变量值。
我们还是用到我们的泰坦尼克号的数据集,同时使用我们上次锦囊分享的知识,对数据进行预处理操作,见下:
# 导入相关库
import pandas as pd
import numpy as np
from pandas import Series,DataFrame
import re
# 导入泰坦尼的数据集
data_train = pd.read_csv("./data/titanic/Train.csv")
# 提取其中几列
data = data_train.loc[:,['PassengerId','Name']]
# 提取称谓
data['Title'] = data['Name'].map(lambda x: re.compile(", (.*?)\.").findall(x)[0])
# 定义一个空字典来收集映射关系
title_Dict = {}
title_Dict.update(dict.fromkeys(['Capt', 'Col', 'Major', 'Dr', 'Rev'], 'Officer'))
title_Dict.update(dict.fromkeys(['Don', 'Sir', 'the Countess', 'Dona', 'Lady'], 'Royalty'))
title_Dict.update(dict.fromkeys(['Mme', 'Ms', 'Mrs'], 'Mrs'))
title_Dict.update(dict.fromkeys(['Mlle', 'Miss'], 'Miss'))
title_Dict.update(dict.fromkeys(['Mr'], 'Mr'))
title_Dict.update(dict.fromkeys(['Master','Jonkheer'], 'Master'))
data['Title'] = data['Title'].map(title_Dict)
data.Title.value_counts()那么接下来我们对字段Title进行独热编码,这里使用get_dummies,生成N个0-1新字段:
# 我们对字段Title进行独热编码,这里使用get_dummies,生成N个0-1新字段
dummies_title = pd.get_dummies(data['Title'], prefix="Title")
data = pd.concat([data,dummies_title], axis=1)
data.head()对了,这里有些同学可能会问,还有一种独热编码出来的是N-1个字段的又是什么?另外这种的话,我们是称为dummy encoding的,也就是哑变量编码,它把任意一个状态位去除,也就是说其中有一类变量值的哑变量表示为全0。更多的内容建议可以百度深入了解哈。
我们在进行特征处理的时候,也有的时候会遇到一些变量,比如说年龄,然后我们想要按照我们想要的阈值进行分类,比如说低于18岁的作为一类,18-30岁的作为一类,那么怎么用Python实现的呢?
是的,我们还是用到我们的泰坦尼克号的数据集,对数据进行预处理操作,见下:
# 导入相关库
import pandas as pd
import numpy as np
from pandas import Series,DataFrame
# 导入泰坦尼的数据集
data_train = pd.read_csv("./data/titanic/Train.csv")
# 修复部分age的值
data_train.loc[(data_train.Age<=1),'Age'] = 1
# 只保留部分值
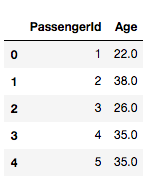
data = data_train.loc[:,['PassengerId','Age']]
data.head()然后,我们编辑代码,按照我们的预期进行分组:
# 确定阈值,写入列表
bins = [0, 12, 18, 30, 50, 70, 100]
data['Age_group'] = pd.cut(data['Age'], bins)
dummies_Age = pd.get_dummies(data['Age_group'], prefix= 'Age')
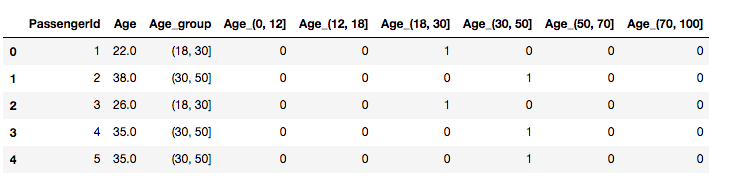
data = pd.concat([data, dummies_Age], axis=1)
data.head()这样子就很神奇了吧,把年龄按照我们的需求进行分组,顺便使用独热编码生成了新的字段。
关于这种衍生变量的方式,理论其实大家应该很早也都听说过了,但是如何在Python里实现,也就是今天在这里分享给大家,其实也很简单,就是调用sklearn的PolynomialFeatures方法,具体大家可以看看下面的demo。
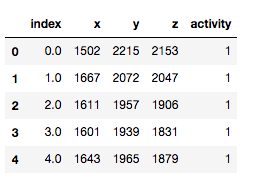
这里使用一个人体加速度数据集,也就是记录一个人在做不同动作时候,在不同方向上的加速度,分别有3个方向,命名为x、y、z。
# 人体胸部加速度数据集,标签activity的数值为1-7
'''
1-在电脑前工作
2-站立、走路和上下楼梯
3-站立
4-走路
5-上下楼梯
6-与人边走边聊
7-站立着说话
'''
import pandas as pd
df = pd.read_csv('./data/activity_recognizer/1.csv', header=None)
df.columns = ['index','x','y','z','activity']
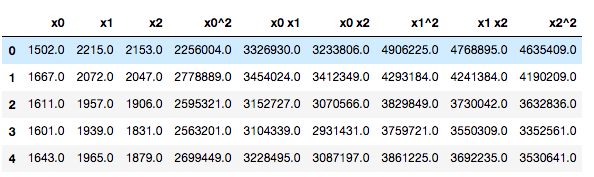
df.head()那么我们可以直接调用刚刚说的办法,然后对于数值型变量多项式的变量扩展,代码如下:
# 扩展数值特征
from sklearn.preprocessing import PolynomialFeatures
x = df[['x','y','z']]
y = df['activity']
poly = PolynomialFeatures(degree=2, include_bias=False, interaction_only=False)
x_poly = poly.fit_transform(x)
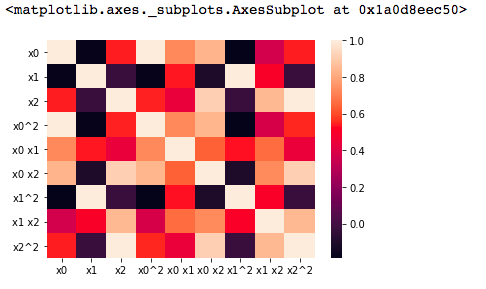
pd.DataFrame(x_poly, columns=poly.get_feature_names()).head()上次的锦囊有提及到如何使用sklearn来实现多项式的扩展来衍生更多的变量,但是我们也知道其实这样子出来的变量之间的相关性是很强的,我们怎么可以可视化一下呢?这里介绍一个热力图的方式,调用corr来实现变量相关性的计算,同时热力图,颜色越深的话,代表相关性越强!
# 人体胸部加速度数据集,标签activity的数值为1-7
'''
1-在电脑前工作
2-站立、走路和上下楼梯
3-站立
4-走路
5-上下楼梯
6-与人边走边聊
7-站立着说话
'''
import pandas as pd
from sklearn.preprocessing import PolynomialFeatures
df = pd.read_csv('./data/activity_recognizer/1.csv', header=None)
df.columns = ['index','x','y','z','activity']
x = df[['x','y','z']]
y = df['activity']
# 多项式扩充数值变量
poly = PolynomialFeatures(degree=2, include_bias=False, interaction_only=False)
x_poly = poly.fit_transform(x)
pd.DataFrame(x_poly, columns=poly.get_feature_names()).head()
# 查看热力图(颜色越深代表相关性越强)
%matplotlib inline
import seaborn as sns
sns.heatmap(pd.DataFrame(x_poly, columns=poly.get_feature_names()).corr())今天我们用的是一个新的数据集,也是在kaggle上的一个比赛,大家可以先去下载一下:
下载地址:https://www.kaggle.com/c/house-prices-advanced-regression-techniques/data
import pandas as pd
import numpy as np
# Plots
import seaborn as sns
import matplotlib.pyplot as plt
# 读取数据集
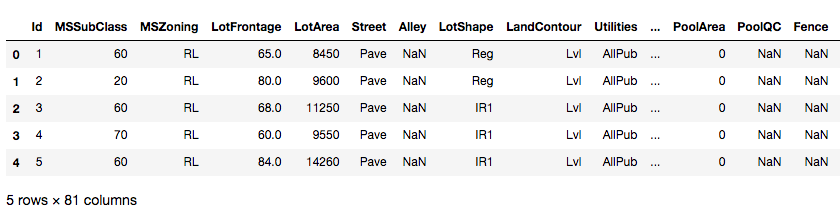
train = pd.read_csv('./data/house-prices-advanced-regression-techniques/train.csv')
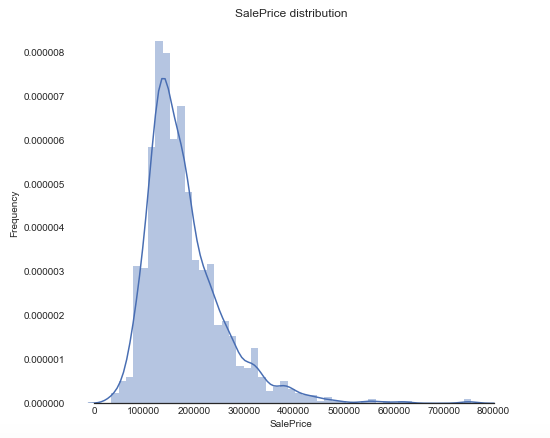
train.head()首先这个是一个价格预测的题目,在开始前我们需要看看分布情况,可以调用以下的方法来进行绘制:
sns.set_style("white")
sns.set_color_codes(palette='deep')
f, ax = plt.subplots(figsize=(8, 7))
#Check the new distribution
sns.distplot(train['SalePrice'], color="b");
ax.xaxis.grid(False)
ax.set(ylabel="Frequency")
ax.set(xlabel="SalePrice")
ax.set(title="SalePrice distribution")
sns.despine(trim=True, left=True)
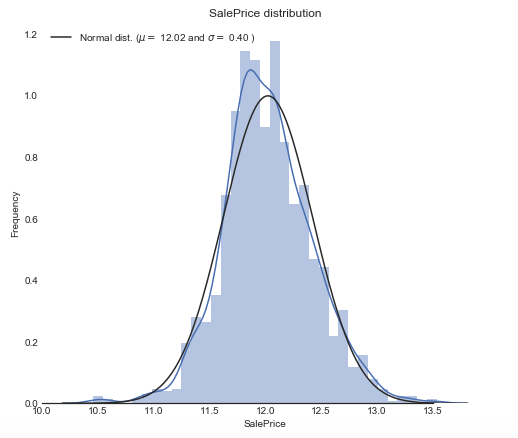
plt.show()我们从结果可以看出,销售价格是右偏,而大多数机器学习模型都不能很好地处理非正态分布数据,所以我们可以应用log(1+x)转换来进行修正。那么具体我们可以怎么用Python代码实现呢?
# log(1+x) 转换
train["SalePrice_log"] = np.log1p(train["SalePrice"])
sns.set_style("white")
sns.set_color_codes(palette='deep')
f, ax = plt.subplots(figsize=(8, 7))
sns.distplot(train['SalePrice_log'] , fit=norm, color="b");
# 得到正态分布的参数
(mu, sigma) = norm.fit(train['SalePrice_log'])
plt.legend(['Normal dist. ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)],
loc='best')
ax.xaxis.grid(False)
ax.set(ylabel="Frequency")
ax.set(xlabel="SalePrice")
ax.set(title="SalePrice distribution")
sns.despine(trim=True, left=True)
plt.show()今天我们用的是一个新的数据集,也是在kaggle上的一个比赛,大家可以先去下载一下:
下载地址:https://www.kaggle.com/c/house-prices-advanced-regression-techniques/data
import pandas as pd
import numpy as np
# Plots
import seaborn as sns
import matplotlib.pyplot as plt
# 读取数据集
train = pd.read_csv('./data/house-prices-advanced-regression-techniques/train.csv')
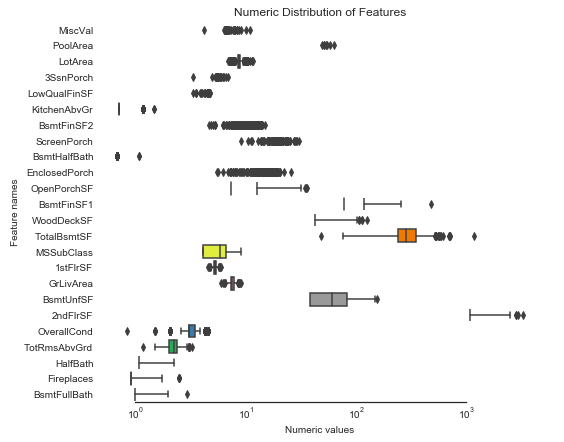
train.head()我们对数据集进行分析,首先我们可以先看看特征的分布情况,看下哪些特征明显就是有数据倾斜的,然后可以找办法解决,因此,第一步就是要有办法找到这些特征。
首先可以通过可视化的方式,画箱体图,然后观察箱体情况,理论知识是:
在箱线图中,箱子的中间有一条线,代表了数据的中位数。箱子的上下底,分别是数据的上四分位数(Q3)和下四分位数(Q1),这意味着箱体包含了50%的数据。因此,箱子的高度在一定程度上反映了数据的波动程度。上下边缘则代表了该组数据的最大值和最小值。有时候箱子外部会有一些点,可以理解为数据中的“异常值”。而对于数据倾斜的,我们叫做“偏态”,与正态分布相对,指的是非对称分布的偏斜状态。在统计学上,众数和平均数之差可作为分配偏态的指标之一:如平均数大于众数,称为正偏态(或右偏态);相反,则称为负偏态(或左偏态)。
# 丢弃y值
all_features = train.drop(['SalePrice'], axis=1)
# 找出所有的数值型变量
numeric_dtypes = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64']
numeric = []
for i in all_features.columns:
if all_features[i].dtype in numeric_dtypes:
numeric.append(i)
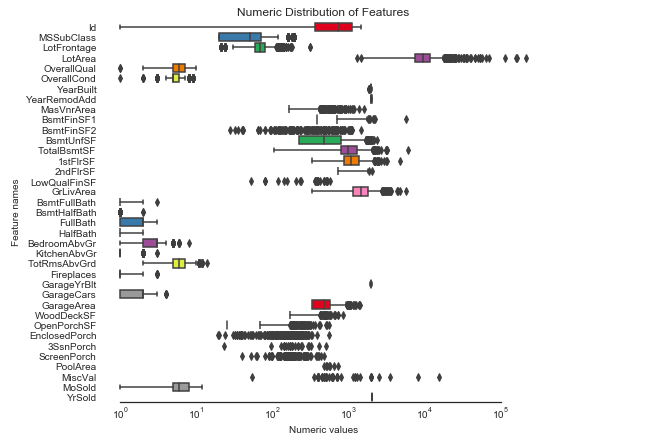
# 对所有的数值型变量绘制箱体图
sns.set_style("white")
f, ax = plt.subplots(figsize=(8, 7))
ax.set_xscale("log")
ax = sns.boxplot(data=all_features[numeric] , orient="h", palette="Set1")
ax.xaxis.grid(False)
ax.set(ylabel="Feature names")
ax.set(xlabel="Numeric values")
ax.set(title="Numeric Distribution of Features")
sns.despine(trim=True, left=True)可以看出有一些特征,有一些数据会偏离箱体外,因此属于数据倾斜。但是,我们从上面的可视化中虽然看出来了,但是想要选出来还是比较麻烦,所以这里引入一个偏态的概念,相对应的有一个指标skew,这个就是代表偏态的系数。
Skewness:描述数据分布形态的统计量,其描述的是某总体取值分布的对称性,简单来说就是数据的不对称程度。
偏度是三阶中心距计算出来的。
(1)Skewness = 0 ,分布形态与正态分布偏度相同。
(2)Skewness > 0 ,正偏差数值较大,为正偏或右偏。长尾巴拖在右边,数据右端有较多的极端值。
(3)Skewness < 0 ,负偏差数值较大,为负偏或左偏。长尾巴拖在左边,数据左端有较多的极端值。
(4)数值的绝对值越大,表明数据分布越不对称,偏斜程度大。
那么在Python里可以怎么实现呢?
# 找出明显偏态的数值型变量
skew_features = all_features[numeric].apply(lambda x: skew(x)).sort_values(ascending=False)
high_skew = skew_features[skew_features > 0.5]
skew_index = high_skew.index
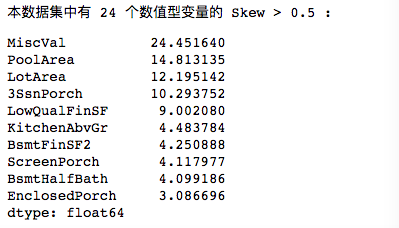
print("本数据集中有 {} 个数值型变量的 Skew > 0.5 :".format(high_skew.shape[0]))
skewness = pd.DataFrame({'Skew' :high_skew})
skew_features.head(10)上一个锦囊,分享了给大家通过skew的方法来找到数据集中有数据倾斜的特征(特征锦囊:怎么找出数据集中有数据倾斜的特征?),那么怎么去修正它呢?正是今天要分享给大家的锦囊!
还是用到房价预测的数据集:
下载地址:https://www.kaggle.com/c/house-prices-advanced-regression-techniques/data
import pandas as pd
import numpy as np
# Plots
import seaborn as sns
import matplotlib.pyplot as plt
# 读取数据集
train = pd.read_csv('./data/house-prices-advanced-regression-techniques/train.csv')
train.head()我们通过上次的知识,知道了可以通过skewness来进行倾斜特征的辨别,那么对于修正它的办法,这里也先分享一个理论知识 —— box-cox转换。
线性回归模型满足线性性、独立性、方差齐性以及正态性的同时,又不丢失信息,此种变换称之为Box—Cox变换。
Box-Cox变换是Box和Cox在1964年提出的一种广义幂变换方法,是统计建模中常用的一种数据变换,用于连续的响应变量不满足正态分布的情况。Box-Cox变换之后,可以一定程度上减小不可观测的误差和预测变量的相关性。Box-Cox变换的主要特点是引入一个参数,通过数据本身估计该参数进而确定应采取的数据变换形式,Box-Cox变换可以明显地改善数据的正态性、对称性和方差相等性,对许多实际数据都是行之有效的。—— 百度百科
在使用前,我们先看看原先倾斜的特征有多少个。
# 丢弃y值
all_features = train.drop(['SalePrice'], axis=1)
# 找出所有的数值型变量
numeric_dtypes = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64']
numeric = []
for i in all_features.columns:
if all_features[i].dtype in numeric_dtypes:
numeric.append(i)
# 找出明显偏态的数值型变量
skew_features = all_features[numeric].apply(lambda x: skew(x)).sort_values(ascending=False)
high_skew = skew_features[skew_features > 0.5]
skew_index = high_skew.index
print("本数据集中有 {} 个数值型变量的 Skew > 0.5 :".format(high_skew.shape[0]))
skewness = pd.DataFrame({'Skew' :high_skew})
skew_features本数据集中有 24 个数值型变量的 Skew > 0.5 :
在Python中怎么使用Box-Cox 转换呢?很简单。
# 通过 Box-Cox 转换,从而把倾斜的数据进行修正
for i in skew_index:
all_features[i] = boxcox1p(all_features[i], boxcox_normmax(all_features[i] + 1))然后我们再看看还有多少个数据倾斜的特征吧!
# 找出明显偏态的数值型变量
skew_features = all_features[numeric].apply(lambda x: skew(x)).sort_values(ascending=False)
high_skew = skew_features[skew_features > 0.5]
skew_index = high_skew.index
print("本数据集中有 {} 个数值型变量的 Skew > 0.5 :".format(high_skew.shape[0]))
skewness = pd.DataFrame({'Skew' :high_skew})本数据集中有 15 个数值型变量的 Skew > 0.5 :
变少了很多,而且如果看他们的skew值,也会发现变小了很多。我们也可以看看转换后的箱体图情况。
# Let's make sure we handled all the skewed values
sns.set_style("white")
f, ax = plt.subplots(figsize=(8, 7))
ax.set_xscale("log")
ax = sns.boxplot(data=all_features[skew_index] , orient="h", palette="Set1")
ax.xaxis.grid(False)
ax.set(ylabel="Feature names")
ax.set(xlabel="Numeric values")
ax.set(title="Numeric Distribution of Features")
sns.despine(trim=True, left=True)PCA算法在数据挖掘中是很基础的降维算法,简单回顾一下定义:
PCA,全称为Principal Component Analysis,也就是主成分分析方法,是一种降维算法,其功能就是把N维的特征,通过转换映射到K维上(K<N),这些由原先N维的投射后的K个正交特征,就被称为主成分。
我们在这里使用的数据集iris,来弄一个demo:
# 导入相关库
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
%matplotlib inline
#解决中文显示问题,Mac
%matplotlib inline
from matplotlib.font_manager import FontProperties
# 设置显示的尺寸
plt.rcParams['font.family'] = ['Arial Unicode MS'] #正常显示中文
# 导入数据集
iris = load_iris()
iris_x, iris_y = iris.data, iris.target
# 实例化
pca = PCA(n_components=2)
# 训练数据
pca.fit(iris_x)
pca.transform(iris_x)[:5,]
# 自定义一个可视化的方法
label_dict = {i:k for i,k in enumerate(iris.target_names)}
def plot(x,y,title,x_label,y_label):
ax = plt.subplot(111)
for label,marker,color in zip(
range(3),('^','s','o'),('blue','red','green')):
plt.scatter(x=x[:,0].real[y == label],
y = x[:,1].real[y == label],
color = color,
alpha = 0.5,
label = label_dict[label]
)
plt.xlabel(x_label)
plt.ylabel(y_label)
leg = plt.legend(loc='upper right', fancybox=True)
leg.get_frame().set_alpha(0.5)
plt.title(title)
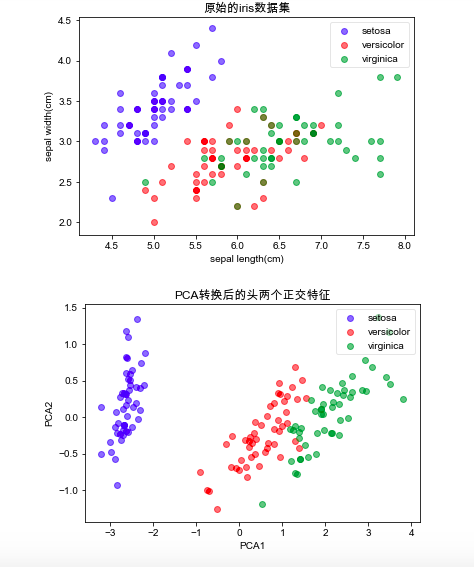
# 可视化
plot(iris_x, iris_y,"原始的iris数据集","sepal length(cm)","sepal width(cm)")
plt.show()
plot(pca.transform(iris_x), iris_y,"PCA转换后的头两个正交特征","PCA1","PCA2")我们通过自定义的绘图函数plot,把不同类别的y值进行不同颜色的显示,从而看出在值域上分布的差异。从原始的特征来看,不同类别之间其实界限并不是十分明显,如上图所示。而进行PCA转换后,可以看出不同类别之间的界限有了比较明显的差异。
LDA算法在数据挖掘中是很基础的算法,简单回顾一下定义:
LDA的全称为Linear Discriminant Analysis, 中文为线性判别分析,LDA是一种有监督学习的算法,和PCA不同。PCA是无监督算法,。LDA是“投影后类内方差最小,类间方差最大”,也就是将数据投影到低维度上,投影后希望每一种类别数据的投影点尽可能的接近,而不同类别的数据的类别中心之间的距离尽可能的大。
我们在这里使用的数据集iris,来弄一个demo:
# 导入相关库
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
%matplotlib inline
#解决中文显示问题,Mac
%matplotlib inline
from matplotlib.font_manager import FontProperties
# 设置显示的尺寸
plt.rcParams['font.family'] = ['Arial Unicode MS'] #正常显示中文
# 导入数据集
iris = load_iris()
iris_x, iris_y = iris.data, iris.target
# 实例化
lda = LinearDiscriminantAnalysis(n_components=2)
# 训练数据
x_lda_iris = lda.fit_transform(iris_x, iris_y)
# 自定义一个可视化的方法
label_dict = {i:k for i,k in enumerate(iris.target_names)}
def plot(x,y,title,x_label,y_label):
ax = plt.subplot(111)
for label,marker,color in zip(
range(3),('^','s','o'),('blue','red','green')):
plt.scatter(x=x[:,0].real[y == label],
y = x[:,1].real[y == label],
color = color,
alpha = 0.5,
label = label_dict[label]
)
plt.xlabel(x_label)
plt.ylabel(y_label)
leg = plt.legend(loc='upper right', fancybox=True)
leg.get_frame().set_alpha(0.5)
plt.title(title)
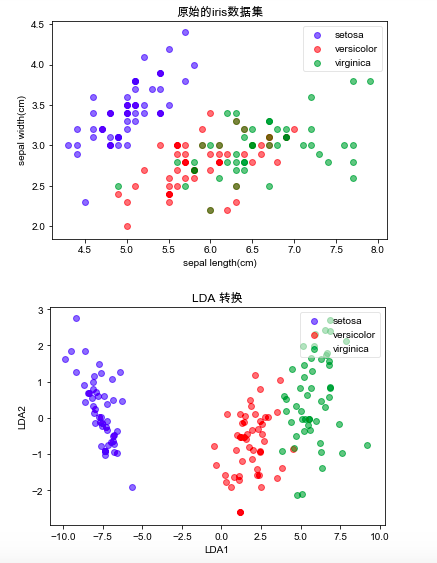
# 可视化
plot(iris_x, iris_y,"原始的iris数据集","sepal length(cm)","sepal width(cm)")
plt.show()
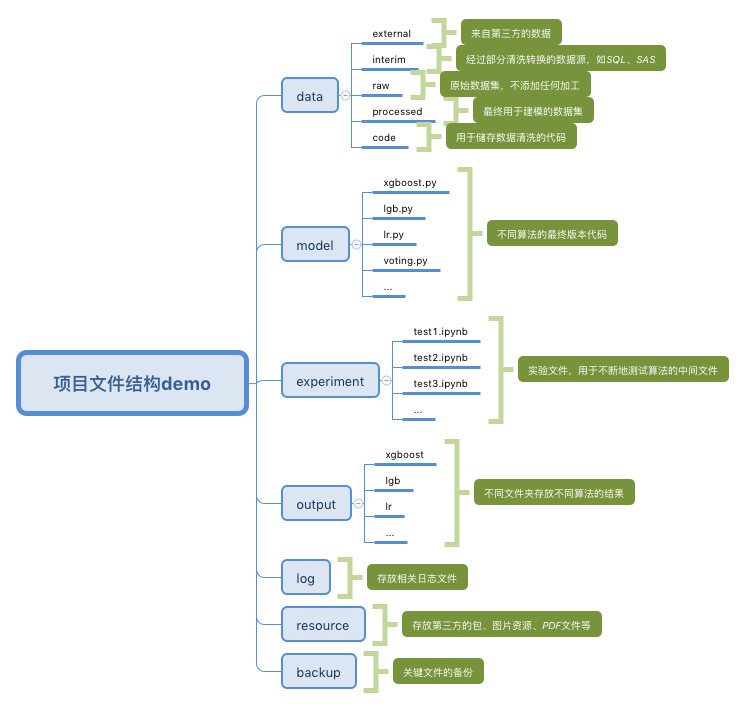
plot(x_lda_iris, iris_y, "LDA Projection", "LDA1", "LDA2")这个专题其实很久之前在我的一篇文章里有比较详细的介绍,可以戳《分享8点超级有用的Python编程建议》,但是今天我还是想把其中的一个内容重点来说一下,大家可以先看看这张图,这个我们在做建模项目时,个人比较推荐的一个建项目文件的demo。
这个项目文件结构是我平时经常用的,会根据项目复杂度自行删减一些内容,不过总体的框架还是差不多的,所以分享给大家参考下呗,因为个人用起来还是蛮不错的,图片里讲了还是比较详细的了,不过我还是挑一些重点来简单解释一下:
- experiment:专门用来存放我们的实验文件,也就是那些不断地测试算法的中间文件。
- model:存放不同算法的最终版本代码的文件夹
- data:存放数据的文件夹,里面还会分不同类别去存放数据,比如external(来自第三方的数据)、interim(经过部分清洗转换的数据源,如SQL、SAS)、raw(原始数据集,不添加任何加工)、processed(最终用于建模的数据集)、code(用于储存数据清洗的代码)
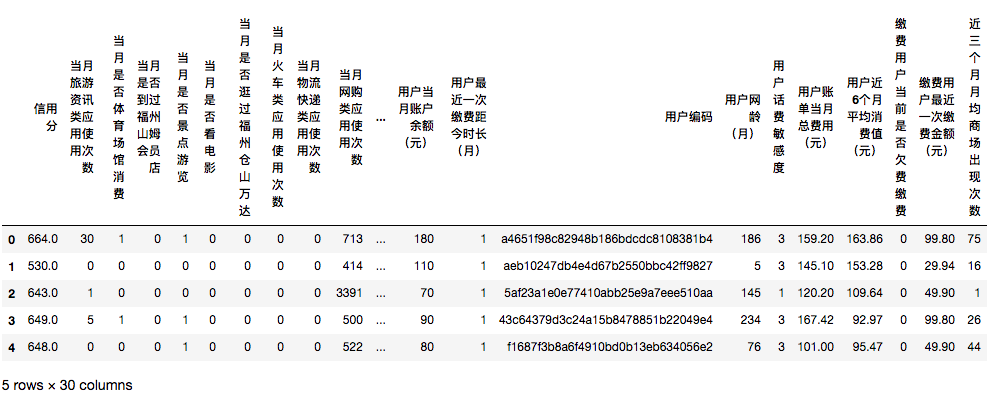
这个专栏停了也有一段时间了,自从上次对之前的内容进行了一次梳理之后,似乎是给自己一个“借口”休息了一阵子,现在感觉还是得重新拿出来继续更新了。
# 导入数据集
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
train = pd.read_csv('./data/Group-Image-of-Consumers/train_dataset.csv')
test = pd.read_csv('./data/Group-Image-of-Consumers/test_dataset.csv')
data = pd.concat([train, test], ignore_index=True)
data.head()我们简单从里面挑选几个数值型变量来看看分布情况吧,画图的技巧这里就不说了,可以参考之前画箱体图的那篇镜囊文章。
# 挑选其中几个变量
feature_list=['当月网购类应用使用次数','当月金融理财类应用使用总次数','当月视频播放类应用使用次数']
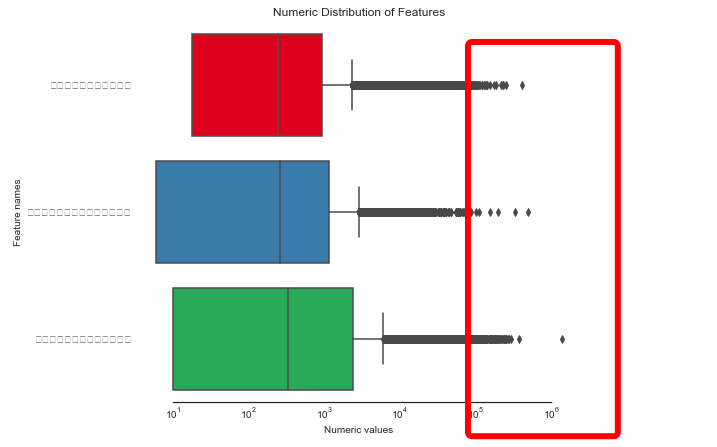
# 绘制箱体图
sns.set_style("white")
f, ax = plt.subplots(figsize=(8, 7))
ax.set_xscale("log")
ax = sns.boxplot(data=data[feature_list] , orient="h", palette="Set1")
ax.xaxis.grid(False)
ax.set(ylabel="Feature names")
ax.set(xlabel="Numeric values")
ax.set(title="Numeric Distribution of Features")
sns.despine(trim=True, left=True)可以看到红色框框圈起来的就是我们的离群点,那么我们可以怎么处理一下呢?这里给大家介绍一个方法,代码如下:
def process(all_data,feature_list):
#处理离群点
for col in feature_list:
ulimit=np.percentile(all_data[col].values, 99.9) #计算一个多维数组的任意百分比分位数
llimit=np.percentile(all_data[col].values, 0.1)
all_data.loc[all_data[col]>ulimit,col]=ulimit # 大于99.9%的直接赋值
all_data.loc[all_data[col]<llimit,col]=llimit
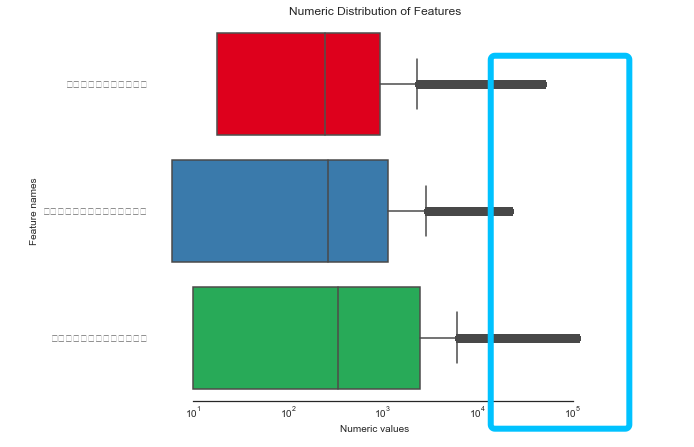
return all_data使用刚刚我们编写的那个方法:
# 使用函数进行极端值的转换
data_new = process(data,feature_list)
# 绘制箱体图
sns.set_style("white")
f, ax = plt.subplots(figsize=(8, 7))
ax.set_xscale("log")
ax = sns.boxplot(data=data_new[feature_list] , orient="h", palette="Set1")
ax.xaxis.grid(False)
ax.set(ylabel="Feature names")
ax.set(xlabel="Numeric values")
ax.set(title="Numeric Distribution of Features")
sns.despine(trim=True, left=True)see!我们的异常值就会被直接“安排”了,是不是很简单呢?其实异常值的处理还是有很大方法的,今天就抛砖引玉一下,更多的方法等待大家去挖掘哦!
第一次接触这两个名词是在做风控模型的时候,老师教我们可以用IV去做变量筛选,IV(Information Value),中文名是信息值,简单来说这个指标的作用就是来衡量变量的预测能力强弱的,然后IV又是WOE算出来的。姑且先不管原理哈,我们先给出来一下结论。
| IV范围 | 变量预测力 |
|---|---|
| <0.02 | 无预测力😯 |
| 0.02~0.10 | 弱👎 |
| 0.10~0.30 | 中等😊 |
| `> 0.30 | 强👍 |
虽然可能这个指标还是很容易就可以使用,但是了解它的原理是十分重要的,这对于我们深入理解变量有很大的帮助。
在开始讲原理前,先约定一下今天会用到的一些代号。
响应/未响应:指的是自变量每个记录对应的目标变量的值,目标变量的值为0或1,一般如果1为响应的话,0就是未响应。
可以看看下面的表格理解一波,变量A是一个连续型变量,值域是v1-vx,当前根据某些分箱方式分成了m组,具体的分组情况如下所示:
WOE是weight of evidence的缩写,是一种编码形式,首先我们要知道WOE是针对类别变量而言的,所以连续性变量需要提前做好分组(这里也是一个很好的考点,也有会说分箱、离散化的,变量优化也可以从这个角度出发)。
先给出数学计算公式,对于第i组的WOE可以这么计算:
从公式上可以看出,第i组的WOE值等于这个组的响应客户占所有响应客户的比例与未响应客户占所有未响应客户的比例的比值取对数。对于上面的公式我们还可以 简单做一下转化:
所以,WOE主要就是体现组内的好坏占比与整体的差异化程度大小,WOE越大,差异越大。
上面我们介绍了如何计算一个分组的WOE值,那么我们就可以把变量所有分组的WOE值给算出来了,对应地,每个分组也有一个IV值,我们叫
计算这个变量的IV值就是这样子就可以了,把每个分组的IV值给加起来。
好了,上面的理论也讲了一些了,还是拿一个实际的变量来计算一下。
我们来假设一个场景,我们需要卖茶叶,然后我们不知道从哪里拿来了一份1000人的营销名单(手机号码),然后就批量添加微信好友,最后有500个手机号码可以成功搜索到微信号的,进而进行了好友添加,最终有100人成功添加到好友了。
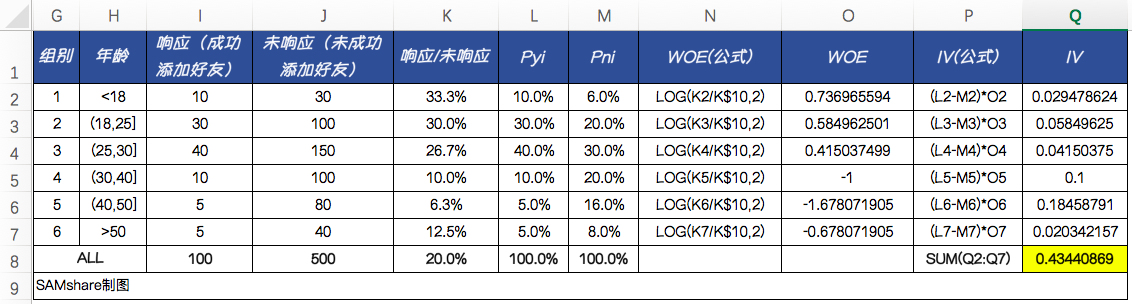
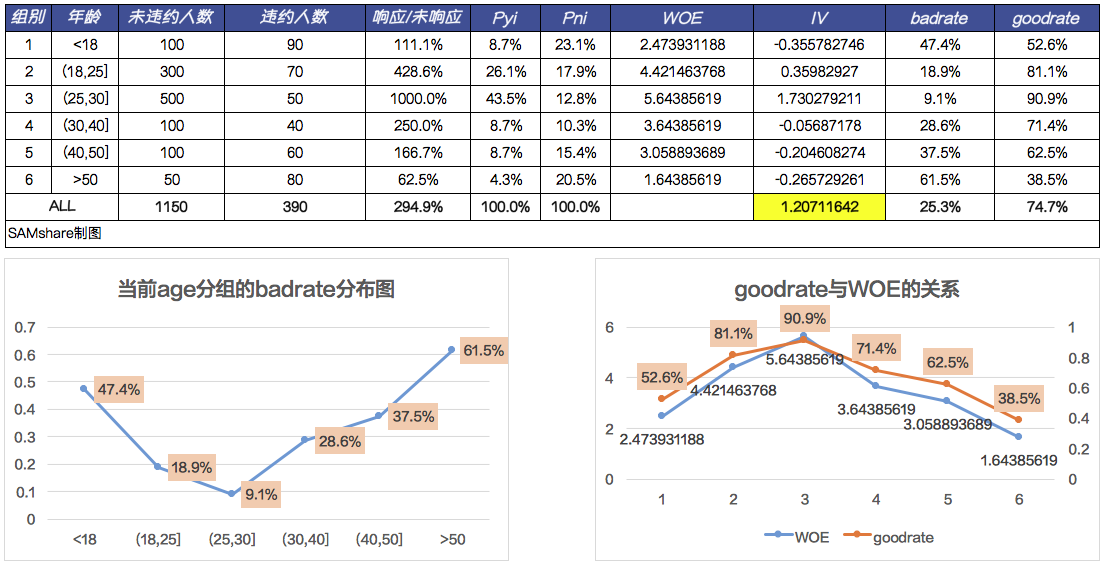
我们这份名单上,有客户的年龄字段,那么我们可以拿来计算一下这个字段对于是否成功添加好友(响应)有多大的预测能力,我们在Excel中进行实现:
可以看出来,这个变量对于我们是否可以成功加到客户微信好友有着很强的预测能力。
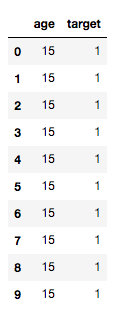
我们知道,针对连续型变量,是需要先转换为类别变量才可以进行IV值的计算的,现在我们把数据导入到Python中,原始变量是连续型变量,那么我们如何在Python里实现IV值的计算呢?如下图:(其中target=1代表响应,target=0代表未响应)
核心代码就是下面的:
def iv_count(data_bad, data_good):
'''计算iv值'''
value_list = set(data_bad.unique()) | set(data_good.unique())
iv = 0
len_bad = len(data_bad)
len_good = len(data_good)
for value in value_list:
# 判断是否某类是否为0,避免出现无穷小值和无穷大值
if sum(data_bad == value) == 0:
bad_rate = 1 / len_bad
else:
bad_rate = sum(data_bad == value) / len_bad
if sum(data_good == value) == 0:
good_rate = 1 / len_good
else:
good_rate = sum(data_good == value) / len_good
iv += (good_rate - bad_rate) * math.log(good_rate / bad_rate,2)
print(value,iv)
return iv那么我们如何使用呢,一步一步来:
测试数据集可以后台回复 'age' 进行获取。
data = pd.read_csv('./data/age.csv')
# 定义必要的参数
feature = data.loc[:,['age']]
labels = data['target']
keep_cols = ['age']
cut_bin_dict = {'age':[0,18,25,30,40,50,100]}按照我们之前Excel相同的分箱逻辑进行分箱:
cut_bin = cut_bin_dict['age']
# 按照分箱阈值分箱,并将缺失值替换成Blank,区分好坏样本
data_bad = pd.cut(feature['age'], cut_bin, right=False).cat.add_categories(['Blank']).fillna('Blank')[labels == 1]
data_good = pd.cut(feature['age'], cut_bin, right=False
).cat.add_categories(['Blank']).fillna('Blank')[labels == 0]
value_list = set(data_bad.unique()) | set(data_good.unique())
value_listiv_series['age'] = iv_count(data_bad, data_good)
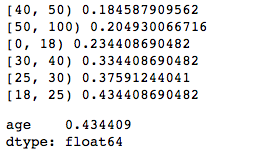
iv_series可以看得出,和我们Excel计算的结果完全一致!
嗯,上面针对单个的变量IV计算是会了,那么如果有一堆需要你计算IV的变量,可以如何处理呢?其实,原理很简单,就是写个循环,这里呢已经写好了一个,大家可以参考一下的。这边有一些细节的东西需要说明一下的。
1)注意区分变量类型,数值型变量和类别型变量要区分对待。
2)注意分组后是否出现某组内的响应(未响应)数量为零的情况,如果为零需要处理一下。
代码放上,大家可以试着运行一下:
def get_iv_series(feature, labels, keep_cols=None, cut_bin_dict=None):
'''
计算各变量最大的iv值,get_iv_series方法出入参如下:
------------------------------------------------------------
入参结果如下:
feature: 数据集的特征空间
labels: 数据集的输出空间
keep_cols: 需计算iv值的变量列表
cut_bin_dict: 数值型变量要进行分箱的阈值字典,格式为{'col1':[value1,value2,...], 'col2':[value1,value2,...], ...}
------------------------------------------------------------
入参结果如下:
iv_series: 各变量最大的IV值
'''
def iv_count(data_bad, data_good):
'''计算iv值'''
value_list = set(data_bad.unique()) | set(data_good.unique())
iv = 0
len_bad = len(data_bad)
len_good = len(data_good)
for value in value_list:
# 判断是否某类是否为0,避免出现无穷小值和无穷大值
if sum(data_bad == value) == 0:
bad_rate = 1 / len_bad
else:
bad_rate = sum(data_bad == value) / len_bad
if sum(data_good == value) == 0:
good_rate = 1 / len_good
else:
good_rate = sum(data_good == value) / len_good
iv += (good_rate - bad_rate) * math.log(good_rate / bad_rate,2)
return iv
if keep_cols is None:
keep_cols = sorted(list(feature.columns))
col_types = feature[keep_cols].dtypes
categorical_feature = list(col_types[col_types == 'object'].index)
numerical_feature = list(col_types[col_types != 'object'].index)
iv_series = pd.Series()
# 遍历数值变量计算iv值
for col in numerical_feature:
cut_bin = cut_bin_dict[col]
# 按照分箱阈值分箱,并将缺失值替换成Blank,区分好坏样本
data_bad = pd.cut(feature[col], cut_bin, right=False).cat.add_categories(['Blank']).fillna('Blank')[labels == 1]
data_good = pd.cut(feature[col], cut_bin, right=False
).cat.add_categories(['Blank']).fillna('Blank')[labels == 0]
iv_series[col] = iv_count(data_bad, data_good)
# 遍历类别变量计算iv值
for col in categorical_feature:
# 将缺失值替换成Blank,区分好坏样本
data_bad = feature[col].fillna('Blank')[labels == 1]
data_good = feature[col].fillna('Blank')[labels == 0]
iv_series[col] = iv_count(data_bad, data_good)
return iv_seriesiv_series = get_iv_series(feature, labels, keep_cols, cut_bin_dict=cut_bin_dict)
iv_series
# age 0.434409记住IV值的预测能力映射:
| IV范围 | 变量预测力 |
|---|---|
| <0.02 | 无预测力😯 |
| 0.02~0.10 | 弱👎 |
| 0.10~0.30 | 中等😊 |
| `> 0.30 | 强👍 |
如果想复现代码,可以从我的公号后台输出 'age' 去获取测试集吧,或者拿自己目前的数据集来玩玩也可以,不过得注意一些细节,转换数据格式。
今天还是讲一下金融风控的相关知识,上一次我们有讲到,如果我们需要计算变量的IV值,从而判断变量的预测能力强弱,是需要对变量进行离散化的,也就是分箱处理。那么,今天就来给大家解释一下其中一种分箱方式 —— 卡方分箱处理。
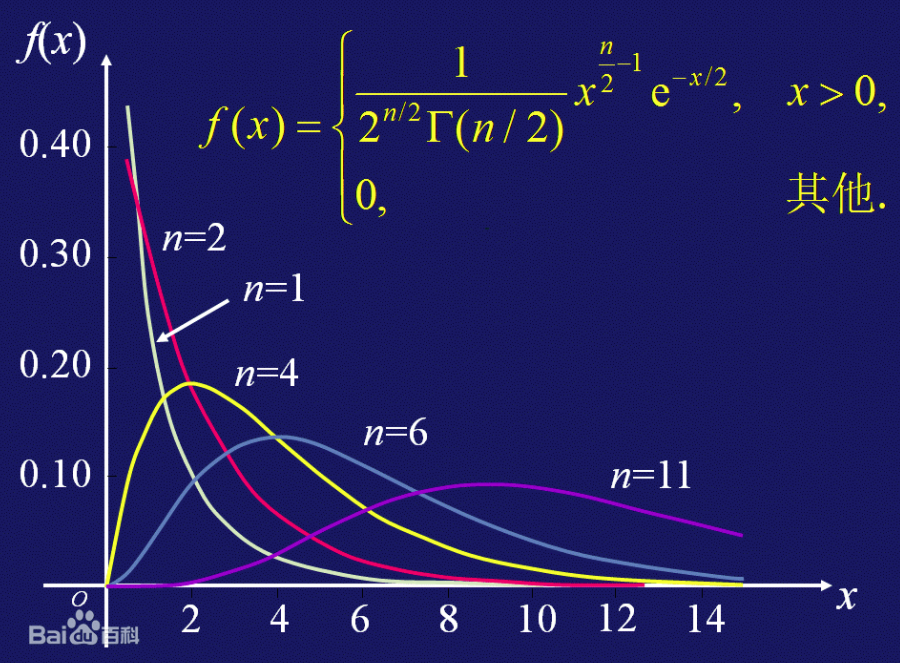
了解卡方分箱,首先需要了解下卡方分布。卡方分布(chi-square distribution, χ2-distribution)是概率统计里常用的一种概率分布,也是统计推断里应用最广泛的概率分布之一,在假设检验与置信区间的计算中经常能见到卡方分布的身影,其定义如下:
若k个相互独立的随机变量$Z_1$,
$Z_2$ ,$Z_3$ , ...,$Z_k$ 满足标准正态分布 N(0,1),那么这k个随机变量的平方和$X=\displaystyle\sum^{k}_{i=1}{Z_i^2}$ 就是服从自由度为k的卡方分布了,一般记作:$X ~ X^2(k)$
其概率密度函数如下所示(图片来自百度百科):
卡方检测是以卡方分布为基础的一种假设检验方法,主要是用于检验分类变量之间的独立性情况。它的基本思想就是根据样本数据推断总体分布与期望分布之间是否存在显著性差异,或者说两个分类变量之间是否相互独立(or是否相关)。
一般的情况下我们会把原假设设置为:观察频数与期望频数之间没有差异,也就是说两个分类变量之间是相互独立不相关的。
实际的应用中我们假设原假设成立,然后计算出卡方值,从而来决策是否需要拒绝原假设,卡方值的计算公式如下:
其中,A为实际频数,E为期望频数,卡方值就是计算实际与期望之间的差异程度大小的量化指标。上面公式结果服从卡方分布,然后我们根据卡方分布、卡方统计量以及自由度,就可以查出p值,如果p值很小,代表观察值与期望值偏离程度很大,那么就需要拒绝原假设,也就是说两个分类变量之间有相关性。
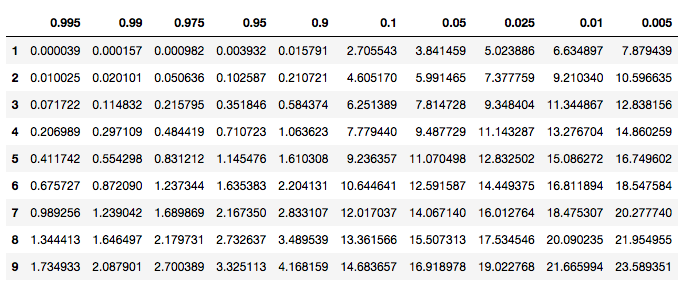
这个概念貌似在大一的时候就有接触过了,可以知道横轴是分位数,纵轴是自由度,然后类似于Python的loc方法,定位到的值就是卡方值了。(比如,要找分位数位0.9,自由度为8的值,查表可知为3.489539
如果想要在Python里生成卡方分布表,可以尝试下面的代码:
# 用Python生成卡方分布临界值表
import numpy as np
import pandas as pd
from scipy.stats import chi2
# chi square distribution
percents = [0.995, 0.990, 0.975, 0.950, 0.900, 0.100, 0.050, 0.025, 0.010, 0.005]
df = pd.DataFrame(np.array([chi2.isf(percents, df=i) for i in range(1, 10)]), columns=percents, index=list(range(1,10)))
df我们有一组数据,是某种病的患者使用了A和B两种不同方案的治疗,所得到的治疗结果,如下表所示,问A、B两种疗法是否有明显差异?
| 组别 | 有效 | 无效 | 合计 | 有效率% |
|---|---|---|---|---|
| A组 | 19 | 24 | 43 | 44.2% |
| B组 | 34 | 10 | 44 | 77.3% |
| 合计 | 53 | 34 | 87 | 60.9% |
这道题其实就是套公式,从上面我了解到要计算卡方值可以有这个公式:
所以,我们先算出每个格子的期望频数:
示例1:A组有效的期望频数:43*53/87=26.20
| 期望频数 | 有效 | 无效 | 合计 | 有效率% |
|---|---|---|---|---|
| A组 | 26.20 | 16.80 | 43 | 60.9% |
| B组 | 26.80 | 17.20 | 44 | 60.9% |
| 合计 | 53 | 34 | 87 | 60.9% |
先建立原假设:A、B两种疗法没有区别。
然后就套入上面的公式:(A为实际频数,E为期望频数)
因为我们选择了其中一个方案,另外一个方案就明确了,所以自由度是1,因此可以查表,自由度为1的,而且卡方值为10.01的分位数是多少了~
查表自由度为1,p=0.05的卡方值为3.841,而此例卡方值10.01>3.841,因此 p < 0.05,说明原假设在0.05的显著性水平下是可以拒绝的,也就是说原假设不成立,也就是两种治疗方案有区别。
上面讲了这么多基础的知识,就是为了引出这一节的内容—— ChiMerge分箱算法。
ChiMerge卡方分箱算法由Kerber于1992提出。它主要包括两个阶段:初始化阶段和自底向上的合并阶段。
首先按照属性值的大小进行排序(对于非连续特征,需要先做数值转换,比如转为坏人率,然后排序),然后每个属性值单独作为一组。
(1)对每一对相邻的组,计算卡方值。
(2)根据计算的卡方值,对其中最小的一对邻组合并为一组。
(3)不断重复(1)和(2)直到计算出的卡方值都不低于事先设定的阈值,或者分组数达到一定的条件(如最小分组数5,最大分组数8)。
值得注意的是,阿Sam之前发现有的实现方法在合并阶段,计算的并非相邻组的卡方值(只考虑在此两组内的样本,并计算期望频数),因为他们用整体样本来计算此相邻两组的期望频数。
了解了原理之后,那么Python如何实现呢?请看下面的代码:
import numpy as np
from scipy.stats import chi
import pandas as pd
from pandas import DataFrame,Series
import scipydef chi3(arr):
'''
计算卡方值
arr:频数统计表,二维numpy数组。
'''
assert(arr.ndim==2)
#计算每行总频数
R_N = arr.sum(axis=1)
#每列总频数
C_N = arr.sum(axis=0)
#总频数
N = arr.sum()
# 计算期望频数 C_i * R_j / N。
E = np.ones(arr.shape)* C_N / N
E = (E.T * R_N).T
square = (arr-E)**2 / E
#期望频数为0时,做除数没有意义,不计入卡方值
square[E==0] = 0
#卡方值
v = square.sum()
return vdef chiMerge(df,col,target,max_groups=None,threshold=None):
'''
卡方分箱
df: pandas dataframe数据集
col: 需要分箱的变量名(数值型)
target: 类标签
max_groups: 最大分组数。
threshold: 卡方阈值,如果未指定max_groups,默认使用置信度95%设置threshold。
return: 包括各组的起始值的列表.
'''
freq_tab = pd.crosstab(df[col],df[target])
#转成numpy数组用于计算。
freq = freq_tab.values
#初始分组切分点,每个变量值都是切分点。每组中只包含一个变量值.
#分组区间是左闭右开的,如cutoffs = [1,2,3],则表示区间 [1,2) , [2,3) ,[3,3+)。
cutoffs = freq_tab.index.values
#如果没有指定最大分组
if max_groups is None:
#如果没有指定卡方阈值,就以95%的置信度(自由度为类数目-1)设定阈值。
if threshold is None:
#类数目
cls_num = freq.shape[-1]
threshold = chi2.isf(0.05,df= cls_num - 1)
while True:
minvalue = None
minidx = None
#从第1组开始,依次取两组计算卡方值,并判断是否小于当前最小的卡方
for i in range(len(freq) - 1):
v = chi3(freq[i:i+2])
if minvalue is None or (minvalue > v): #小于当前最小卡方,更新最小值
minvalue = v
minidx = i
#如果最小卡方值小于阈值,则合并最小卡方值的相邻两组,并继续循环
if (max_groups is not None and max_groups< len(freq) ) or (threshold is not None and minvalue < threshold):
#minidx后一行合并到minidx
tmp = freq[minidx] + freq[minidx+1]
freq[minidx] = tmp
#删除minidx后一行
freq = np.delete(freq,minidx+1,0)
#删除对应的切分点
cutoffs = np.delete(cutoffs,minidx+1,0)
else: #最小卡方值不小于阈值,停止合并。
break
return cutoffsdef value2group(x,cutoffs):
'''
将变量的值转换成相应的组。
x: 需要转换到分组的值
cutoffs: 各组的起始值。
return: x对应的组,如group1。从group1开始。
'''
#切分点从小到大排序。
cutoffs = sorted(cutoffs)
num_groups = len(cutoffs)
#异常情况:小于第一组的起始值。这里直接放到第一组。
#异常值建议在分组之前先处理妥善。
if x < cutoffs[0]:
return 'group1'
for i in range(1,num_groups):
if cutoffs[i-1] <= x < cutoffs[i]:
return 'group{}'.format(i)
#最后一组,也可能会包括一些非常大的异常值。
return 'group{}'.format(num_groups)def calWOE(df ,var ,target):
'''
计算WOE编码
param df:数据集pandas.dataframe
param var:已分组的列名,无缺失值
param target:响应变量(0,1)
return:编码字典
'''
eps = 0.000001 #避免除以0
gbi = pd.crosstab(df[var],df[target]) + eps
gb = df[target].value_counts() + eps
gbri = gbi/gb
gbri['woe'] = np.log(gbri[1]/gbri[0])
return gbri['woe'].to_dict()def calIV(df,var,target):
'''
计算IV值
param df:数据集pandas.dataframe
param var:已分组的列名,无缺失值
param target:响应变量(0,1)
return:IV值
'''
eps = 0.000001 #避免除以0
gbi = pd.crosstab(df[var],df[target]) + eps
gb = df[target].value_counts() + eps
gbri = gbi/gb
gbri['woe'] = np.log(gbri[1]/gbri[0])
gbri['iv'] = (gbri[1] - gbri[0])*gbri['woe']
return gbri['iv'].sum()cutoffs = chiMerge(data,'MAX_AMOUNT','target',max_groups=8)
'''
PS:绝大数情况下,会将缺失值NaN归类到最后一组,如果不想这么简单粗暴的,需要在最开始的时候对缺失值进行填充。
'''
data['MAX_AMOUNT_chigroup'] = data['MAX_AMOUNT'].apply(value2group,args=(cutoffs,))
r = data.loc[:,['MAX_、AMOUNT','MAX_AMOUNT_chigroup','target']]
woe_map = calWOE(data,'MAX_AMOUNT_chigroup','target')
iv = calIV(data,'MAX_AMOUNT_chigroup','target')
iv[1] Python评分卡建模—卡方分箱(1)
[2] Python评分卡建模—卡方分箱(2)之代码实现
[3] python评分卡建模—实现WOE编码及IV值计算
今天我们来讲讲一个理论知识,也是老生常谈的内容,在模型开发相关岗位中出场率较高的,那就是L1与L2正则化了,这个看似简单却十分重要的概念,还是需要深入了解的。网上有蛮多的学习资料,今天我就着自己的理解也写一下笔记。📒
从西瓜书📖里我们可以了解到正则项的作用,那就是降低模型过拟合的风险,通常常用的有L1范数正则化与L2范数正则化,作为单独一项(正则项)加入到损失函数中,也可以自己作为损失函数。🐝
在了解L1和L2范数之前,我们可以先来了解一下范数(norm)的定义,根据参考文献[2]的说明:
A norm is a mathematical thing that is applied to a vector (like the vector
βabove). The norm of a vector maps vector values to values in[0,∞). In machine learning, norms are useful because they are used to express distances: this vector and this vector are so-and-so far apart, according to this-or-that norm.
简单来说也就是范数其实在 [0,∞)范围内的值,是向量的投影大小,在机器学习中一般会勇于衡量向量的距离。范数有很多种,我们常见的有L1-norm和L2-norm,其实还有L3-norm、L4-norm等等,所以抽象来表示,我们会写作Lp-norm,一般表示为
$||x||p = \displaystyle (\sum^{}{i}{|x_i|^p})^{1/p}$
对于上面这个抽象的公式,如果我们代入p值,
若p为1,则就是我们常说的L1-norm:
$||x||1 = \displaystyle \sum^{}{i}{|x_i|} = |x_1|+|x_2|+...+|x_i|$
若p为2,则是我们常说的L2-norm:
$||x||2 = \displaystyle \sqrt{(\sum^{}{i}{|x_i|^2})} = \displaystyle \sqrt{x1^2+x2^2+...+x_i^2}$
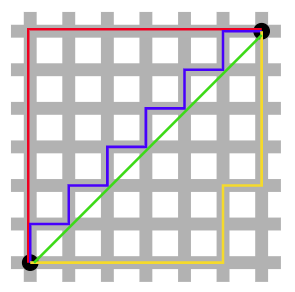
我们引用文章里的图片,L2-norm的距离就是两个黑点之间的绿线,而另外的3条线,都是L1-norm的大小。
在上面我们有提及到,L1、L2范数可以用于损失函数里的一个正则化项,作用就是降低模型复杂度,减小过拟合的风险。这里的正则化项,存在的目的就是作为一个“惩罚项”,对损失函数中的某一些参数做一些限制,是结构风险最小化策略的体现,就是选择经验风险(平均损失函数)和模型复杂度同时较小的模型。
针对线性回归模型,假设对其代价函数里加入正则化项,其中L1和L2正则化项的表示分别如下所示,其中λ >= 0,是用来平衡正则化项和经验风险的系数。
(1)使用L1范数正则化,其模型也被叫作Lasso回归(Least Absolute Shrinkage and Selection Operator,最小绝对收缩选择算子)。
(2)使用L2范数正则化,其模型被叫做Ridge回归,中文为岭回归。
上面介绍的L1和L2范数正则化都有着降低过拟合风险的功能,但它们有什么不同?我们到底应该选择哪一个呢,两者之间各有什么优势和适用场景?别急,我们一一来展开讲讲。
首先,我们从上面那张二维的图可以看出,对于L2-norm,其解是唯一的,也就是绿色的那条;而对于L1-norm,其解不唯一,因此L1正则化项,其计算难度通常会高于L2的。
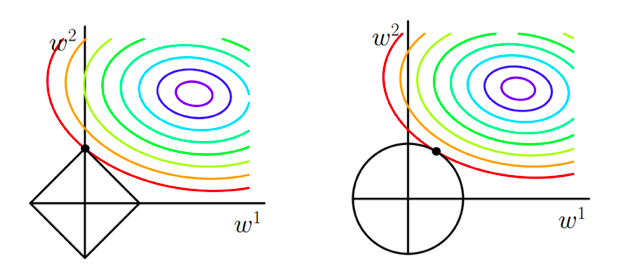
其次,L1通常是比L2更容易得到稀疏输出的,会把一些不重要的特征直接置零,至于为什么L1正则化为什么更容易得到稀疏解,可以看下图:
上图代表的意思就是目标函数-平方误差项的等值线和L1、L2范数等值线(左边是L1),我们正则化后的代价函数需要求解的目标就是在经验风险和模型复杂度之间的平衡取舍,在图中形象地表示就是黑色线与彩色线的交叉点。
对于L1范数,其图形为菱形,二维属性的等值线有4个角(高维的会有更多),“突出来的角”更容易与平方误差项进行交叉,而这些“突出来的角”都是在坐标轴上,即W1或则W2为0;
而对于L2范数,交叉点一般都是在某个象限中,很少有直接在坐标轴上交叉的。
因此L1范数正则化项比L2的更容易得到稀疏解。
直接上结论:
1)因为L1范数正则化项的“稀疏解”特性,L1更适合用于特征选择,找出较为“关键”的特征,而把一些不那么重要的特征置为零。
2)L2范数正则化项可以产生很多参数值很小的模型,也就是说这类的模型抗干扰的能力很强,可以适应不同的数据集,适应不同的“极端条件”。
讲完了作为正则化项的内容了,那么讲讲L1、L2范数作为损失函数的情况。假设我们有一个线性回归模型,我们需要评估模型的效果,很常规的,我们会用“距离”来衡量误差!
若使用L1-norm来衡量距离,那就是我们的LAD(Least Absolute Deviation,最小绝对偏差),其优化的目标函数如下:
实际意义上的解释就是预测值与真实值之间的绝对值。
若使用L2-norm,那就是我们的LSE(Least Squares Error,最小二乘误差),其优化的目标函数如下:
针对两者的差异,可以看下表:
L1损失函数的结果更具鲁棒性,也就是说对于异常值更加不敏感。而根据其范数“天性”,L2的求解更为简单与“唯一”。
[1] Differences between L1 and L2 as Loss Function and Regularization
http://www.chioka.in/differences-between-l1-and-l2-as-loss-function-and-regularization/
[2] L1 Norms versus L2 Norms
https://www.kaggle.com/residentmario/l1-norms-versus-l2-norms
-
✍️ 背景交代
-
🎥 WOE回顾
-
🤔 LR模型的入参一定要WOE吗?
-
🤔 WOE不单调可以进LR模型吗?
-
针对不同类型的变量
-
为什么需要WOE具备单调性
-
-
🏆 结论复盘
今天我们来讲讲一个金融风控里的“常识点”,就是那种我们习以为常但若要讲出个所以然来比较困难的点,正如标题所言:**WOE前的分箱一定要单调吗?**🤔
相信每一个在金融风控领域做过模型的人,应该对分箱满足badrate单调性有一定的认知,特别是在用逻辑回归做A卡的时候,老司机们会经常对我们说变量要满足单调性,当变量单调了,再进行WOE转换,然后作为LR的入参喂给模型,简单训练一下就收工。但作为一个合格的风控建模大师,仅仅知道这些套路还是不够的,我们需要进一步去思考一下当中的原理,或者说是更进一步去追问一下自己:
LR模型的入参一定要WOE吗?
WOE转化前的变量分箱结果的badrate一定需要满足单调性吗?
连续变量难道就不可以直接进LR模型吗?
希望大家在阅读完本篇文章后,多多少少可以对上面的问题有一定的了解~
在我们开始拆解问题前,有一个知识点需要回顾一下,那就是WOE。
WOE是weight of evidence的缩写,是一种编码形式,首先我们要知道WOE是针对类别变量而言的,所以连续性变量需要提前做好分组(这里也是一个很好的考点,也有会说分箱、离散化的,变量优化也可以从这个角度出发)。
先给出数学计算公式,对于第i组的WOE可以这么计算:
从公式上可以看出,第i组的WOE值等于这个组的响应客户占所有响应客户的比例与未响应客户占所有未响应客户的比例的比值取对数。对于上面的公式我们还可以 简单做一下转化:
所以,WOE主要就是体现组内的好坏占比与整体的差异化程度大小,WOE越大,差异越大。
更多的内容可以浏览一下之前的文章《特征锦囊:彻底了解一下WOE和IV》。
The answer is no!并非所有LR的入参都需要WOE的,也可以是直接原始值入模型的。但存在即合理,为什么大家都在说要对变量进行WOE编码呢?我们可以引出下面两个问题:
- 什么情况下用WOE比较合适?
- 以及用WOE有什么好处
我们知道,在风控领域的变量可以大致分为两类,就是数值型变量以及类别型变量,前者就是类似于年龄、逾期天数等,后者就是职业类别、行业类别等。
针对类别型变量,我们很容易可以想到使用one-hot编码来,但是这种编码方式有一定的缺陷,那就是对于枚举值特别多的变量,独热编码之后十分稀疏从而特征空间很大,另外如果丢弃一部分维度则会造成信息丢失,指不定这些是关键的信息。以上的信息说明了放入LR中很难有很好的效果。
而针对数值型变量,很多同学则会有更大的疑问,那就是为什么要分箱然后又进行WOE转换这么麻烦,反正都可以直接入模型的,何必多此一举?
当然了!这个想法也是没错的,在本小节开头也已经说明了,并非要求所有的变量都要进行WOE编码然后进入模型。而什么情况下十分适合WOE转换呢,那就是变量本身与y值并非存在直接线性关系的时候。
我们看上面的图,“年龄”这个字段经常性地会出现在我们的A卡模型里,作为预测一个客户信用水平的衡量指标。我们可以清楚知道,age这个变量的badrate分布,经常性会呈现“U型”,业务解释就是:年轻人和老年人的还款能力会比中年人的要低,风险也因此更高。从统计角度看,年龄与违约率,便不是一个线性关系!
我们回忆一下LR模型(Logistic Regression),从本质上讲,LR就是经过对训练集的学习,得到一组权值w,当有新的一组数据x输入时,根据公式计算出结果,然后经过Sigmoid函数判断这个数据所属的类别。
假如我们的年龄就是上面的x1,并且模型只有一个变量,那么随着x1的变大,$h_w(x)$的值也会不断变大,而不是像上图一样呈现“U型”,说明了这是一个非线性的问题,但如果我们对年龄进行WOE转换,就可以看到如右图所示的那样,随着WOE的增大,goodrate也增大这种线性关系(badrate=1-goodrate,因此和badrate也是线形关系)。
以上也是使用WOE编码的一个最大好处,也就是把badrate呈现非线性的变量转换为线形,便于理解也便于后续模型求解。此外,WOE编码还有一个好处,那就是具有“容错性”,因为WOE编码其实也可以理解为需要预先分箱,那么对于异常值没那么敏感,对于单个变量的异常波动不会有太大反应。
那么我们回到最初的问题,那就是如标题所说的:WOE前的分箱一定要单调吗?结论是不一定需要单调。要深入了解这答案,我们可以看看下面两个讨论:
1)针对类别变量😋
类别变量可以分有序和无序变量。
针对有序类别变量,比如像学历,我们分箱的时候要保证原始顺序的前提下,进行不同原始组别的合并,完成分箱,然后需要看分箱的badrate单调性,最后才来看WOE单调性情况。
针对无序类别变量,无序类别变量又可以根据枚举值的多少拆分为两类:多枚举无序类别变量和少枚举无序类别变量。无论是哪一种,我们都可以根据对每个枚举值的badrate统计得到其量化指标,然后根据badrate进行适当的类别合并,完成分箱操作,这时候的分箱结果,天然单调!而针对少枚举无序类别变量,我们还可以根据业务认识,进行类别的合并,比如像中国大区字段(华南、华北等),WOE编码后,也不做严格的单调性要求。
2)针对数值变量😆
进行合适的分箱算法进行分箱后的bin,需要满足badrate单调性,然后才进行WOE编码。不过呢,这个也不是严格要求的。
WOE不一定都需要是单调的,只要从业务角度可以解释得通,那就没有问题!就好像上面的那个栗子,年龄字段,WOE就不是单调的,但从业务上可以解释得通,那就没有问题!
如果从业务上解释是需要单调性,但分组后的WOE并没有单调,那么这时候有两条路可以选择,一是重新分组然后重新计算WOE,二是放弃这个变量。
最后提一下,如果不单调的变量不进行WOE编码直接进入LR模型,一般都是很难求解的,因为很难找到一个线性公式来描述关系。
1)LR模型的入参不一定都要WOE转换,直接进行模型也是可以的,只是遇上不单调的变量会比较难求解罢了,可选择丢弃。
2)使用WOE编码的一个最大好处是把badrate呈现非线性的变量转换为线形,便于理解也便于后续模型求解,进行了WOE编码的模型对于异常值没那么敏感,单个变量的异常波动不会对模型造成很大反应。
3)WOE并不一定都需要是单调的,只要从业务角度可以解释得通即可。
1、到底什么是不平衡数据
2、处理不平衡数据的理论方法
3、Python里有什么包可以处理不平衡样本
4、Python中具体如何处理失衡样本
印象中很久之前有位朋友说要我写一篇如何处理不平衡数据的文章,整理相关的理论与实践知识(可惜本人太懒了,现在才开始写),于是乎有了今天的文章。失衡样本在我们真实世界中是十分常见的,那么我们在机器学习(ML)中使用这些失衡样本数据会出现什么问题呢?如何处理这些失衡样本呢?以下的内容希望对你有所帮助!
失衡数据发生在分类应用场景中,在分类问题中,类别之间的分布不均匀就是失衡的根本,假设有个二分类问题,target为y,那么y的取值范围为0和1,当其中一方(比如y=1)的占比远小于另一方(y=0)的时候,就是失衡样本了。
那么到底是需要差异多少,才算是失衡呢,根本Google Developer的说法,我们一般可以把失衡分为3个程度:
- 轻度:20-40%
- 中度:1-20%
- 极度:<1%
一般来说,失衡样本在我们构建模型的时候看不出什么问题,而且往往我们还可以得到很高的accuracy,为什么呢?假设我们有一个极度失衡的样本,y=1的占比为1%,那么,我们训练的模型,会偏向于把测试集预测为0,这样子模型整体的预测准确性就会有一个很好看的数字,如果我们只是关注这个指标的话,可能就会被骗了。
在我们开始用Python处理失衡样本之前,我们先来了解一波关于处理失衡样本的一些理论知识,前辈们关于这类问题的解决方案,主要包括以下:
- 从数据角度:通过应用一些欠采样or过采样技术来处理失衡样本。欠采样就是对多数类进行抽样,保留少数类的全量,使得两类的数量相当,过采样就是对少数类进行多次重复采样,保留多数类的全量,使得两类的数量相当。但是,这类做法也有弊端,欠采样会导致我们丢失一部分的信息,可能包含了一些重要的信息,过采样则会导致分类器容易过拟合。当然,也可以是两种技术的相互结合。
- 从算法角度:算法角度的解决方案就是可以通过对每类的训练实例给予一定权值的调整。比如像在SVM这样子的有参分类器中,可以应用grid search(网格搜索)以及交叉验证(cross validation)来优化C以及gamma值。而对于决策树这类的非参数模型,可以通过调整树叶节点上的概率估计从而实现效果优化。
此外,也有研究员从数据以及算法的结合角度来看待这类问题,提出了两者结合体的AdaOUBoost(adaptive over-sampling and undersampling boost)算法,这个算法的新颖之处在于自适应地对少数类样本进行过采样,然后对多数类样本进行欠采样,以形成不同的分类器,并根据其准确度将这些子分类器组合在一起从而形成强大的分类器,更多的请参考:
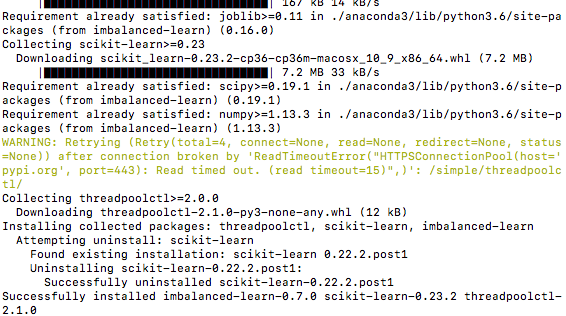
这里介绍一个很不错的包,叫 imbalanced-learn,大家可以在电脑上安装一下使用。
官方文档:https://imbalanced-learn.readthedocs.io/en/stable/index.html
pip install -U imbalanced-learn
使用上面的包,我们就可以实现样本的欠采样、过采样,并且可以利用pipeline的方式来实现两者的结合,十分方便,我们下一节来简单使用一下吧!
为了更好滴理解,我们引入一个数据集,来自于UCI机器学习存储库的营销活动数据集。(数据集大家可以自己去官网下载:https://archive.ics.uci.edu/ml/machine-learning-databases/00222/ 下载bank-additional.zip 或者到公众号后台回复关键字“bank”来获取吧。)
我们在完成imblearn库的安装之后,就可以开始简单的操作了(其余更加复杂的操作可以直接看官方文档),以下我会从4方面来演示如何用Python处理失衡样本,分别是:
🌈1、随机欠采样的实现
🌈2、使用SMOTE进行过采样
🌈3、欠采样和过采样的结合(使用pipeline)
🌈4、如何获取最佳的采样率?
# 导入相关的库(主要就是imblearn库)
from collections import Counter
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
import pandas as pd
import numpy as np
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)
from sklearn.svm import SVC
from sklearn.metrics import classification_report, roc_auc_score
from numpy import mean
# 导入数据
df = pd.read_csv(r'./data/bank-additional/bank-additional-full.csv', ';') # '';'' 为分隔符
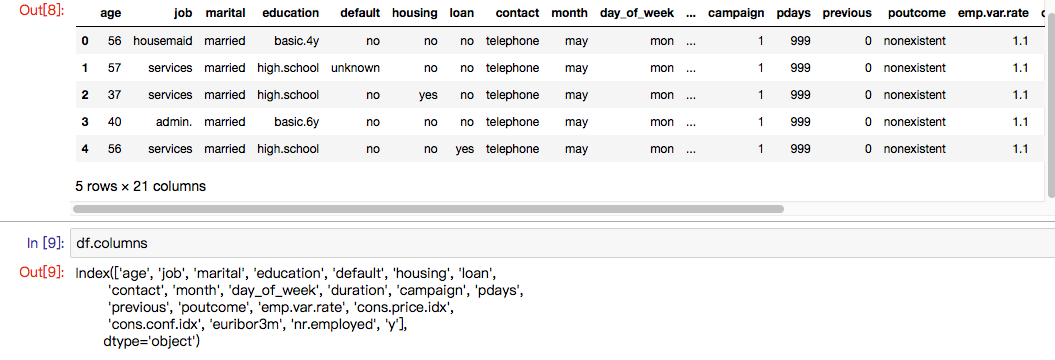
df.head()数据集是葡萄牙银行的某次营销活动的数据,其营销目标就是让客户订阅他们的产品,然后他们通过与客户的电话沟通以及其他渠道获取到的客户信息,组成了这个数据集。
关于字段释义,可以看下面的截图:
我们可以大致看看数据集是不是失衡样本:
df['y'].value_counts()/len(df)
#no 0.887346
#yes 0.112654
#Name: y, dtype: float64可以看出少数类的占比为11.2%,属于中度失衡样本。
# 只保留数值型变量(简单操作)
df = df.loc[:,
['age', 'duration', 'campaign', 'pdays',
'previous', 'emp.var.rate', 'cons.price.idx',
'cons.conf.idx', 'euribor3m', 'nr.employed','y']]
# target由 yes/no 转为 0/1
df['y'] = df['y'].apply(lambda x: 1 if x=='yes' else 0)
df['y'].value_counts()
#0 36548
#1 4640
#Name: y, dtype: int64欠采样在imblearn库中也是有方法可以用的,那就是 under_sampling.RandomUnderSampler,我们可以使用把方法引入,然后调用它。可见,原先0的样本有21942,欠采样之后就变成了与1一样的数量了(即2770),实现了50%/50%的类别分布。
# 1、随机欠采样的实现
# 导入相关的方法
from imblearn.under_sampling import RandomUnderSampler
# 划分因变量和自变量
X = df.iloc[:,:-1]
y = df.iloc[:,-1]
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.40)
# 统计当前的类别占比情况
print("Before undersampling: ", Counter(y_train))
# 调用方法进行欠采样
undersample = RandomUnderSampler(sampling_strategy='majority')
# 获得欠采样后的样本
X_train_under, y_train_under = undersample.fit_resample(X_train, y_train)
# 统计欠采样后的类别占比情况
print("After undersampling: ", Counter(y_train_under))
# 调用支持向量机算法 SVC
model=SVC()
clf = model.fit(X_train, y_train)
pred = clf.predict(X_test)
print("ROC AUC score for original data: ", roc_auc_score(y_test, pred))
clf_under = model.fit(X_train_under, y_train_under)
pred_under = clf_under.predict(X_test)
print("ROC AUC score for undersampled data: ", roc_auc_score(y_test, pred_under))
# Output:
#Before undersampling: Counter({0: 21942, 1: 2770})
#After undersampling: Counter({0: 2770, 1: 2770})
#ROC AUC score for original data: 0.603521152028
#ROC AUC score for undersampled data: 0.829234085179🌈2、使用SMOTE进行过采样
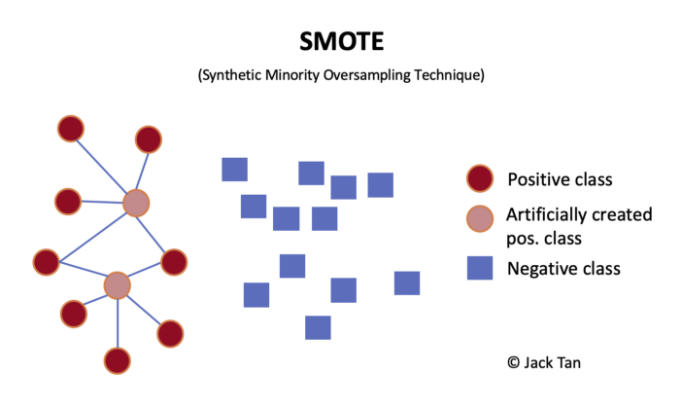
过采样技术中,SMOTE被认为是最为流行的数据采样算法之一,它是基于随机过采样算法的一种改良版本,由于随机过采样只是采取了简单复制样本的策略来进行样本的扩增,这样子会导致一个比较直接的问题就是过拟合。因此,SMOTE的基本思想就是对少数类样本进行分析并合成新样本添加到数据集中。
算法流程如下:
(1)对于少数类中每一个样本x,以欧氏距离为标准计算它到少数类样本集中所有样本的距离,得到其k近邻。
(2)根据样本不平衡比例设置一个采样比例以确定采样倍率N,对于每一个少数类样本x,从其k近邻中随机选择若干个样本,假设选择的近邻为xn。
(3)对于每一个随机选出的近邻xn,分别与原样本按照如下的公式构建新的样本。
# 2、使用SMOTE进行过采样
# 导入相关的方法
from imblearn.over_sampling import SMOTE
# 划分因变量和自变量
X = df.iloc[:,:-1]
y = df.iloc[:,-1]
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.40)
# 统计当前的类别占比情况
print("Before oversampling: ", Counter(y_train))
# 调用方法进行过采样
SMOTE = SMOTE()
# 获得过采样后的样本
X_train_SMOTE, y_train_SMOTE = SMOTE.fit_resample(X_train, y_train)
# 统计过采样后的类别占比情况
print("After oversampling: ",Counter(y_train_SMOTE))
# 调用支持向量机算法 SVC
model=SVC()
clf = model.fit(X_train, y_train)
pred = clf.predict(X_test)
print("ROC AUC score for original data: ", roc_auc_score(y_test, pred))
clf_SMOTE= model.fit(X_train_SMOTE, y_train_SMOTE)
pred_SMOTE = clf_SMOTE.predict(X_test)
print("ROC AUC score for oversampling data: ", roc_auc_score(y_test, pred_SMOTE))
# Output:
#Before oversampling: Counter({0: 21980, 1: 2732})
#After oversampling: Counter({0: 21980, 1: 21980})
#ROC AUC score for original data: 0.602555700614
#ROC AUC score for oversampling data: 0.844305732561🌈3、欠采样和过采样的结合(使用pipeline)
那如果我们需要同时使用过采样以及欠采样,那该怎么做呢?其实很简单,就是使用 pipeline来实现。
# 3、欠采样和过采样的结合(使用pipeline)
# 导入相关的方法
from imblearn.over_sampling import SMOTE
from imblearn.under_sampling import RandomUnderSampler
from imblearn.pipeline import Pipeline
# 划分因变量和自变量
X = df.iloc[:,:-1]
y = df.iloc[:,-1]
# 定义管道
model = SVC()
over = SMOTE(sampling_strategy=0.4)
under = RandomUnderSampler(sampling_strategy=0.5)
steps = [('o', over), ('u', under), ('model', model)]
pipeline = Pipeline(steps=steps)
# 评估效果
scores = cross_val_score(pipeline, X, y, scoring='roc_auc', cv=5, n_jobs=-1)
score = mean(scores)
print('ROC AUC score for the combined sampling method: %.3f' % score)
# Output:
#ROC AUC score for the combined sampling method: 0.937🌈4、如何获取最佳的采样率?
在上面的栗子中,我们都是默认经过采样变成50:50,但是这样子的采样比例并非最优选择,因此我们引入一个叫 最佳采样率的概念,然后我们通过设置采样的比例,采样网格搜索的方法去找到这个最优点。
# 4、如何获取最佳的采样率?
# 导入相关的方法
from imblearn.over_sampling import SMOTE
from imblearn.under_sampling import RandomUnderSampler
from imblearn.pipeline import Pipeline
# 划分因变量和自变量
X = df.iloc[:,:-1]
y = df.iloc[:,-1]
# values to evaluate
over_values = [0.3,0.4,0.5]
under_values = [0.7,0.6,0.5]
for o in over_values:
for u in under_values:
# define pipeline
model = SVC()
over = SMOTE(sampling_strategy=o)
under = RandomUnderSampler(sampling_strategy=u)
steps = [('over', over), ('under', under), ('model', model)]
pipeline = Pipeline(steps=steps)
# evaluate pipeline
scores = cross_val_score(pipeline, X, y, scoring='roc_auc', cv=5, n_jobs=-1)
score = mean(scores)
print('SMOTE oversampling rate:%.1f, Random undersampling rate:%.1f , Mean ROC AUC: %.3f' % (o, u, score))
# Output:
#SMOTE oversampling rate:0.3, Random undersampling rate:0.7 , Mean ROC AUC: 0.938
#SMOTE oversampling rate:0.3, Random undersampling rate:0.6 , Mean ROC AUC: 0.936
#SMOTE oversampling rate:0.3, Random undersampling rate:0.5 , Mean ROC AUC: 0.937
#SMOTE oversampling rate:0.4, Random undersampling rate:0.7 , Mean ROC AUC: 0.938
#SMOTE oversampling rate:0.4, Random undersampling rate:0.6 , Mean ROC AUC: 0.937
#SMOTE oversampling rate:0.4, Random undersampling rate:0.5 , Mean ROC AUC: 0.938
#SMOTE oversampling rate:0.5, Random undersampling rate:0.7 , Mean ROC AUC: 0.939
#SMOTE oversampling rate:0.5, Random undersampling rate:0.6 , Mean ROC AUC: 0.938
#SMOTE oversampling rate:0.5, Random undersampling rate:0.5 , Mean ROC AUC: 0.938从结果日志来看,最优的采样率就是过采样0.5,欠采样0.7。
最后,想和大家说的是没有绝对的套路,只有合适的套路,无论是欠采样还是过采样,只有合适才最重要。还有,欠采样的确会比过采样“省钱”哈(从训练时间上很直观可以感受到)。
[1] SMOTE算法 https://www.jianshu.com/p/13fc0f7f5565
[2] How to deal with imbalanced data in Python
最新的发布内容请关注个人微信公众号哈~