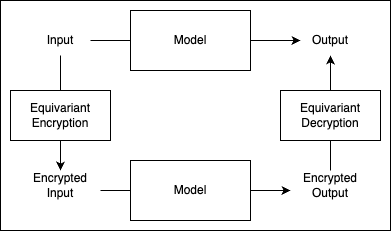
At Nesa, privacy is a critical objective. On our path toward decentralized AI, we confronted a key challenge: how can we perform inference on neural networks without exposing the underlying input and output data to external parties? Traditional approaches, such as differential privacy or homomorphic encryption (HE), while conceptually strong, fall short in practical deployments for complex neural architectures. These methods can struggle to handle non-linear operations efficiently, often imposing substantial computational overhead that makes them challenging to integrate into real-time or large-scale systems.
A snapshot of Equivariant Encryption's properties versus homomorphic encryption:
| Feature | Equivariant Encryption (EE) | Homomorphic Encryption (HE) |
|---|---|---|
| Latency Overhead | None (0) | Very High |
| Non-Linear Operations | Handles Exact | Approximation Needed |
| User Key Control | Direct & Custom | Schema-Defined |
| Cryptographic Hardness | Massive Combinatorial Complexity | Standard Hardness Assumptions |
Zero overhead: EE provides the same latency as plaintext inference, no slowdowns.
128k factorial: EE indicates a massive combinatorial complexity, contributing to the strongest security guarantees.
We investigated multiple methodologies to ensure end-to-end data privacy within the Nesa network. Differential privacy seeks to obscure sensitive details by adding statistical noise, but it cannot fully prevent inference on raw data once it is processed by a model. Homomorphic encryption, on the other hand, is mathematically elegant: it permits computations directly on encrypted data. This is achieved through operations that are homomorphic to addition and multiplication, enabling algebraic manipulation of ciphertexts that, once decrypted, yield the correct plaintext results. Such a property is exceptionally appealing in scenarios like outsourced cloud computations, where one can perform inference off-site without revealing the sensitive inputs.
However, standard HE schemes are tailored around arithmetic operations. Neural networks, especially those with layers like attention mechanisms, activation functions, or normalization steps, do not map cleanly onto ring or field operations alone. Adapting HE to these complex transformations typically incurs prohibitive computational cost, slowing inference to impractical speeds.
Despite this, the conceptual promise of HE—running inference on encrypted data without decryption—prompted us to seek an alternative. We aimed to preserve the protective qualities of encrypted computation while working around the bottlenecks introduced by non-linear neural functions.
Our solution is Equivariant Encryption (EE). The term equivariance signifies a change in representation that preserves the operational structure from the model’s perspective. In other words, we transform the input data into an encrypted domain where the neural network’s computations can be carried out as though it were processing plaintext, all while maintaining the secrecy of the underlying information.
Rather than relying exclusively on arithmetic operations compatible with HE, EE integrates specialized transformations designed around the internal properties of neural networks. We exploit the known architecture, layer composition, and input-output mappings of the model to construct a system in which each step of inference operates correctly on encrypted inputs. This approach avoids expensive retraining on encrypted datasets. Instead, by following a set of mathematical guidelines, we can generate a new variant of the model that works with our encryption schema in a matter of seconds.
Formally, given some plaintext
Crucially, the complexity of inference under EE does not surpass that of the unencrypted version. Each forward pass through the network involves approximately the same computational cost as before. Thus, inference latency remains unchanged, a significant advantage compared to conventional HE-based techniques.
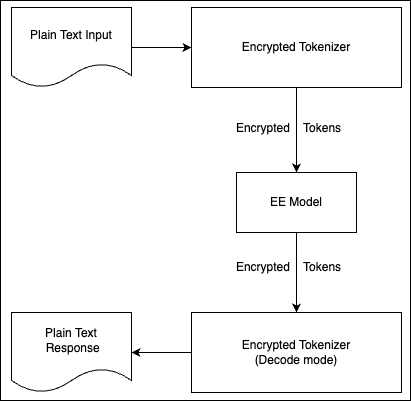
To illustrate this with a tangible example, consider transformer-based models like ChatGPT, Claude, or Llama. These models employ tokenizers to convert text into discrete tokens, each mapped to an integer token id. Under EE, we implement a specialized tokenizer that produces a different, encrypted set of token ids. The network, now adapted to EE, treats these encrypted token ids as standard inputs. It processes them identically to how it would process normal tokens, ultimately returning encrypted output tokens that can be decrypted locally by the user. The following diagram outlines this workflow:
In this setup, all data traveling over the network remains encrypted, and the transformations that produce and consume these tokens are carefully chosen to deny any straightforward method for recovering the plaintext. The attacker sees only encrypted tokens and a model variant designed to operate on that encrypted space, providing no direct, low-cost avenue to extract the original information.
Below is a more detailed breakdown of how Equivariant Encryption matches or outperforms the expectations we have from traditional Homomorphic Encryption methods:
| Property | Homomorphic Encryption (HE) | Equivariant Encryption (EE) |
|---|---|---|
| Data Confidentiality (Server Blindness) | The server never sees plaintext data. | The server never sees plaintext data. |
| End-to-End Encrypted Computation | Operations should be fully on encrypted data, no intermediate decryptions. | EE models run directly on encrypted tokens. No intermediate decryptions are required. |
| User-Controlled Encryption | Users should hold keys and control encryption/decryption. | Only the user can map plaintext to transformed tokens using the EE tokenizer as a private key. |
| Preservation of Accuracy | The decrypted output should match the result of plaintext inference. | EE ensures final results are identical to plaintext inference outputs, with no accuracy loss. |
| Support for Arbitrary Model Structures | HE struggles with non-linearities and complex NN layers. | EE is designed for modern neural architectures and preserves non-linearities. |
| Minimal Performance Overhead | HE incurs large computational overhead. | EE imposes no overhead; inference latency matches that of the underlying model on plaintext data. |
| No Approximation of Functions | HE may require approximations of complex operations. | EE avoids approximations, preserving exact neural network functions post-transformation. |
| Scalability to Large Models | Handling large models under HE is impractical. | EE scales naturally with large models without any computational penalties. |
| Compatibility with Existing Pipelines | HE often requires extensive pipeline modifications. | EE requires a one-time transformation, after which pipelines operate as normal. |
| Clear Security Model & Robustness | HE has strong theoretical foundations. | EE provides a massively complex, secure combinatorial search space, making brute-force attacks impossible. |
We invite the community to examine and test the security claims of our Equivariant Encryption approach. As part of our commitment to transparency and continual refinement, we have organized a contest encouraging participants to probe for weaknesses and demonstrate potential exploits.
For details, please visit: https://github.com/nesaorg/Equivariant-Encryption-for-AI/blob/main/CONTEST.md