Original artwork
Transformed anamorphic version
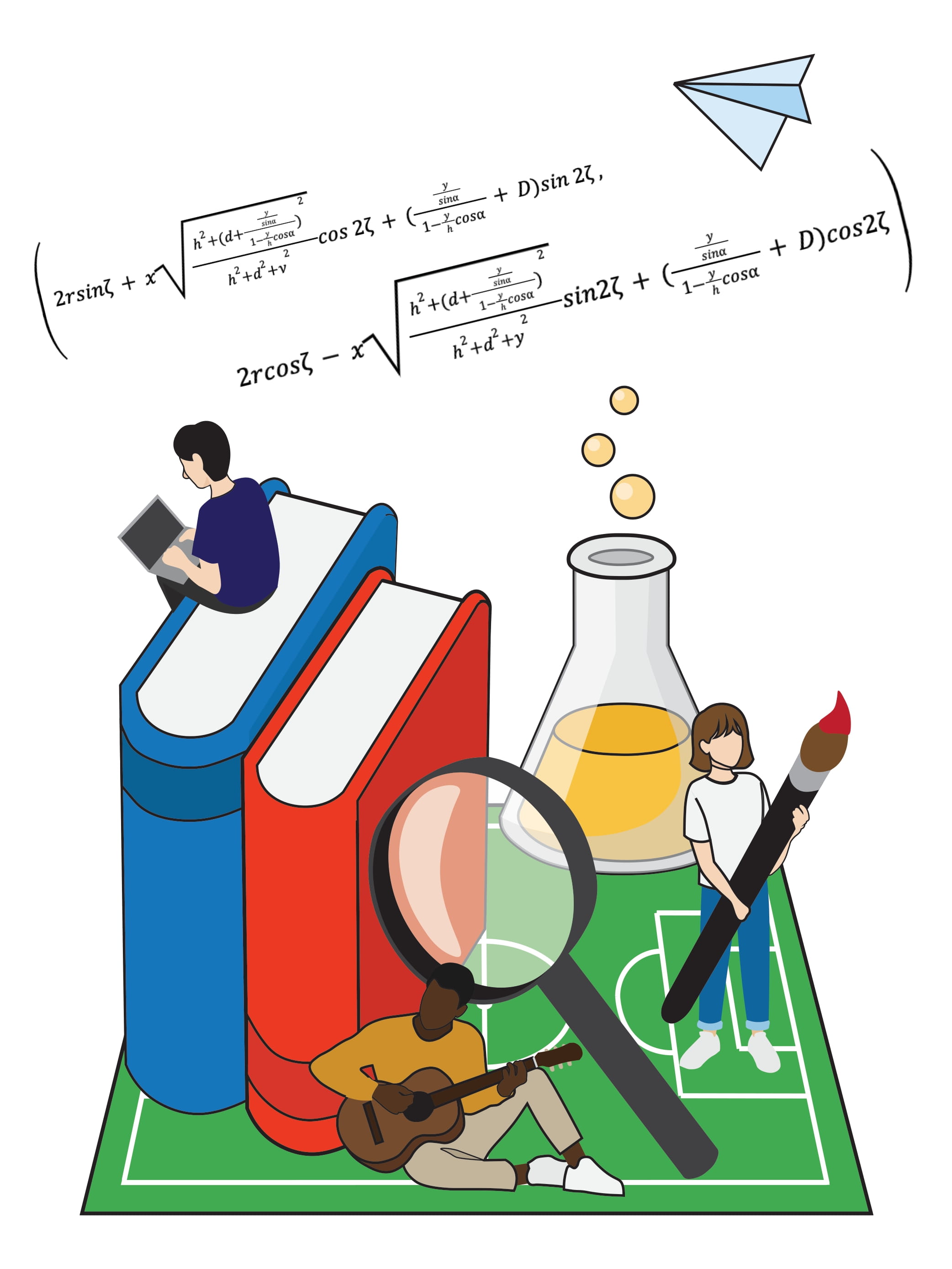
This Wolfram Mathematica notebook transforms ordinary images into cylindrical catoptric anamorphosis - a specialized form of art where distorted images reveal their true form when viewed in a cylindrical mirror. The program implements precise mathematical transformations derived from analytic geometry and trigonometry to achieve this effect.
This code formed the core of my IB Mathematics Extended Essay (May 2023 session), where I investigated the mathematical principles behind cylindrical catoptric anamorphosis. The essay not only derived the mathematical framework for creating these transformations but also demonstrated their practical application.
While writing the extended essay, I wanted to take it beyond traditional academic boundaries. Instead of concluding with theoretical equations, I envisioned creating something that would bring together mathematics and art in a way that people could experience directly. While most cylindrical anamorphic artworks are small-scale artworks, I was determined to create something truly special, that will last even after my graduation.
This vision evolved into a months-long collaborative effort that united multiple departments at my high school:
- The Engineering Department engineered and installed a 1-meter tall cylindrical mirror
- The Art Department and Art Club brought their creative expertise to the large-scale mural
- The Mathematics Department, particularly my advisor, provided crucial guidance and facilitated communications with school faculty and executives
The final installation remains exhibited at my high school to this day, and the project earned the school's "Exemplary Eagle" title for its interdisciplinary nature and scale.
Original artwork
Transformed anamorphic version
Transformed anamorphic version
Transformed anamorphic version
The program in this repository contains the mathematical transformations that made this artwork possible.