2020秋季学期信息安全原理课程大作业
分两次作业
- 64位DES加密
- 128位RSA加密(用于加密DES的密钥)
A. DES简介
数据加密标准(英语:Data Encryption Standard,缩写为 DES)是一种对称密钥加密块密码算法,1976年被美国联邦政府的国家标准局确定为联邦资料处理标准(FIPS),随后在国际上广泛流传开来。它基于使用56位密钥的对称算法。这个算法因为包含一些机密设计元素,相对短的密钥长度以及怀疑内含美国国家安全局(NSA)的后门而在开始时有争议,DES因此受到了强烈的学院派式的审查,并以此推动了现代的块密码及其密码分析的发展。
DES现在已经不是一种安全的加密方法,主要因为它使用的56位密钥过短。1999年1月,distributed.net与电子前哨基金会合作,在22小时15分钟内即公开破解了一个DES密钥。也有一些分析报告提出了该算法的理论上的弱点,虽然在实际中难以应用。为了提供实用所需的安全性,可以使用DES的派生算法3DES来进行加密,虽然3DES也存在理论上的攻击方法。DES标准和3DES标准已逐渐被高级加密标准(AES)所取代。另外,DES已经不再作为国家标准科技协会(前国家标准局)的一个标准。
但DES中采用的很多策略是其他高级算法基础,熟悉和掌握DES的加解密过程对学习和了解现代密码学有重要意义。
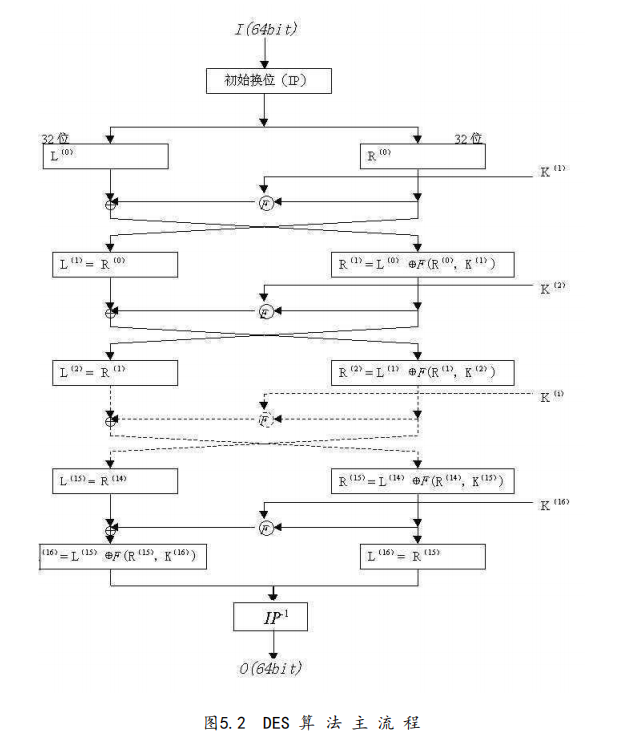
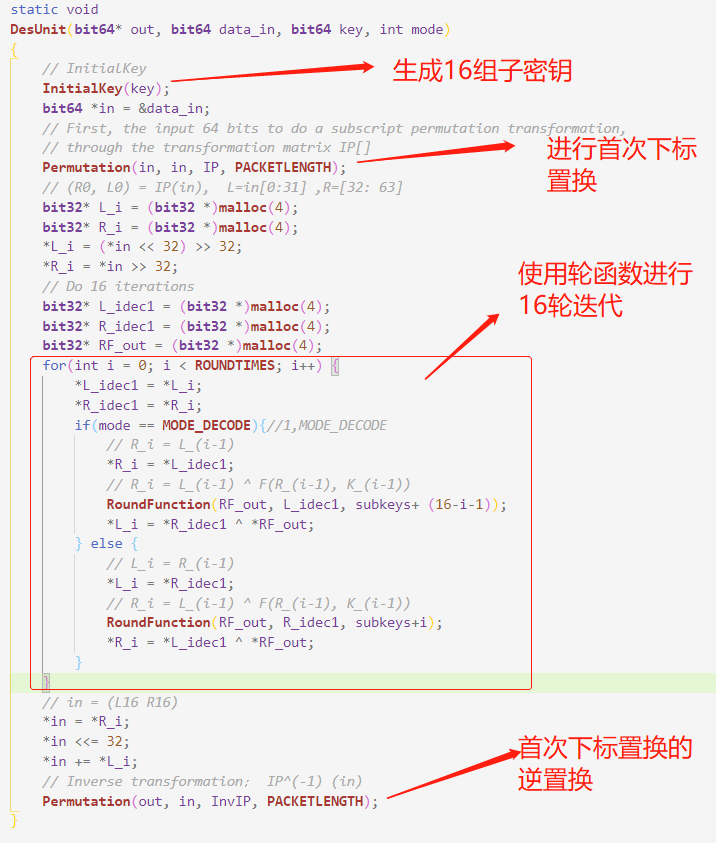
- 初始化密钥,用主密钥生成16组子密钥
- 初始换位(使用矩阵$IP[64]$),把输出分为两个32bits的组$(R0, L0)= IP(in)$
- 按照下述式子,使用轮函数进行16次迭代
-
将两个32bits的组重新合并为64bits,然后使用$IP^{-1}[64]$进行逆置换
-
输出即为64bits的密文
-
加密过程采用CBC模式,即明文组先和上一个密文组进行异或: $$ M[i] = \left{ \begin{aligned} &M[i] \oplus Y[i-1]&&i\geq1\ &M[i] \oplus IV&&i=0\ \end{aligned} \right. $$
与加密过程一致。只是子密钥的使用顺序与加密过程相反,同时把$L,R$互换即可,即: $$ \begin{aligned} &R_i=L_{i-1}\ &L_iR_{i-1}\oplus F(L_{i-1},K_{i-1}) \end{aligned} $$
-
在终端输入如下指令,打印HELP
$ des.exe
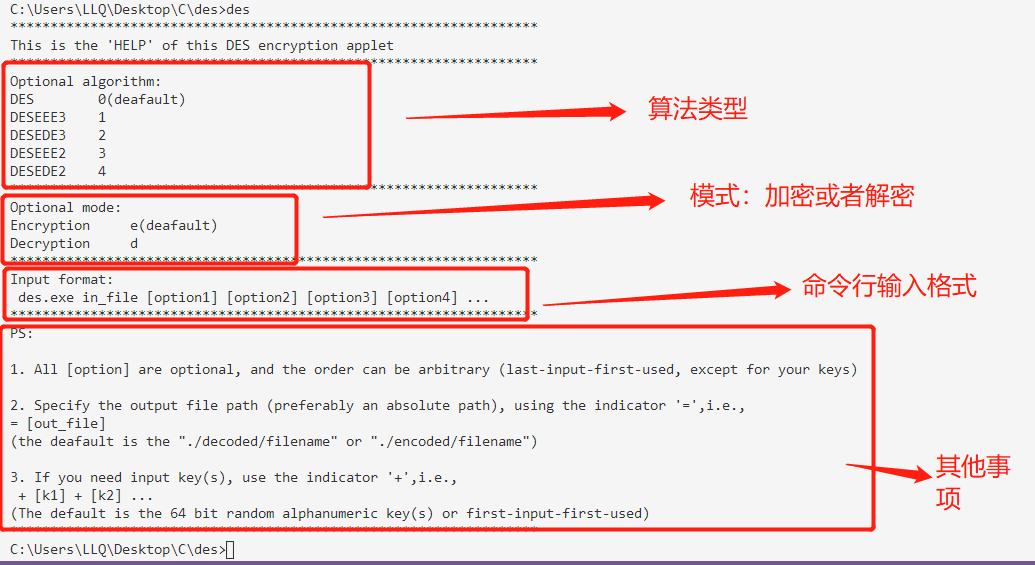
-
在终端输入如下指令,运行程序
$ des.exe in_file [option1] [option2] [option3] [option4] ...
- in_file , 输入文件的路径,最好是绝对路径
-
[option], 4种可选选项(均可以忽略,如忽略即选择默认设置)
-
输出文件的路径:,使用
= out_path。默认是./encoded/原文件名或者./decoded/原文件名 -
加/解密算法:使用
0,1,2,3,4。默认为0 -
加密还是解密:前者使用
e,后者使用d。默认是e,即加密 -
密钥:使用
+ k1 + k2 + k3,密钥个数视算法类型而定。默认是根据算法类型自动生成简单字母数字8Bytes即64-bit密钥
-
输出文件的路径:,使用
例:
$ des.exe .data/data1.jpg d 1 + 12345678 + 12345678 + 12345678作用:使用三个密钥,对文件
.data/data1.jpg使用算法1(DESEEE3),进行解密,并讲结果文件输出到默认路径./decoded/data1.jpg.
- 在终端执行下述命令,编译C文件(如已经编译,生成.exe文件可忽略这一步)
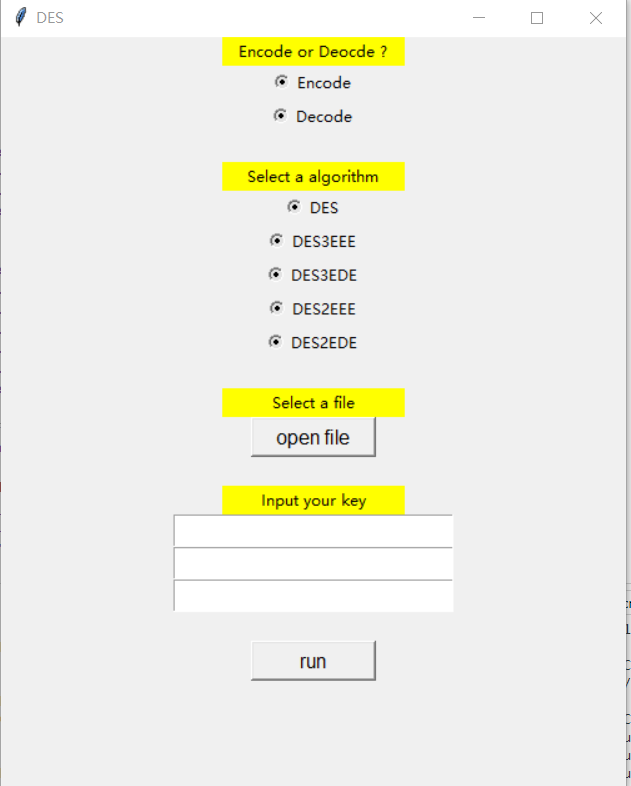
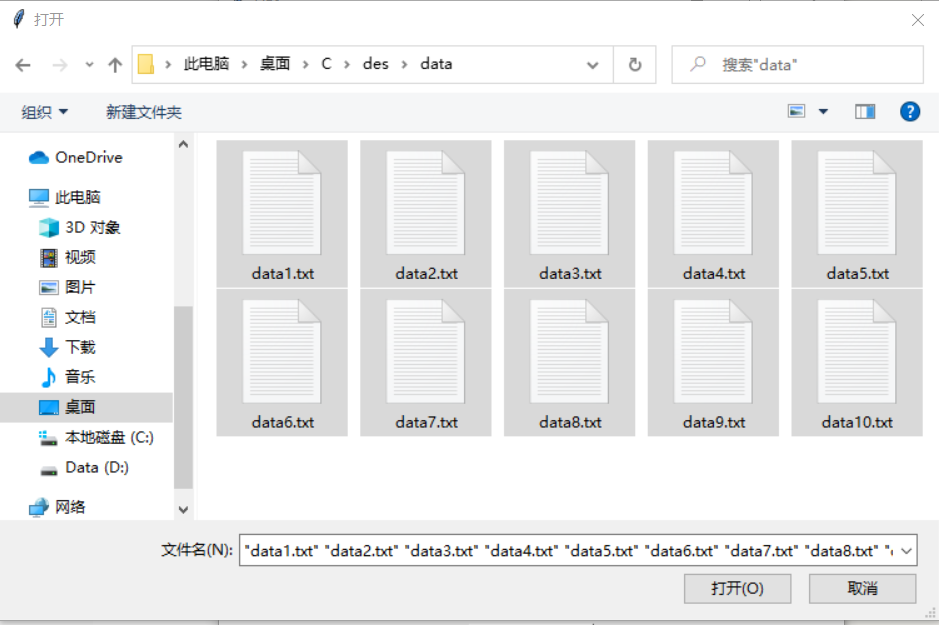
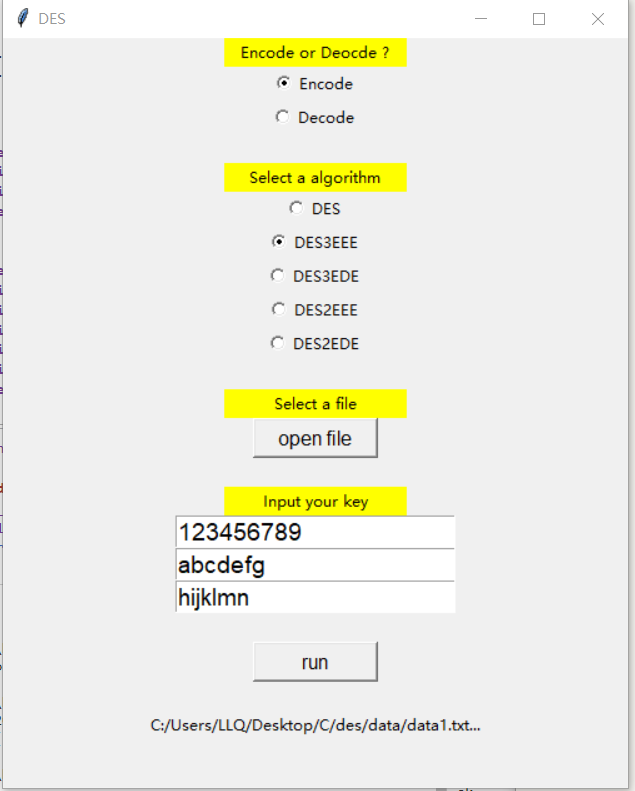
$ make 2. 运行python脚本ui.py,运行结果被如下图所示
加密结果输出项目目录下,/des/encoded/
解密结果输出到项目录,/des/decoded/
- 操作系统:Win10-64bit
- 编译器:gcc version 8.1.0 (x86_64-posix-seh-rev0, Built by MinGW-W64 project) .
- 编程语言:C、Python
des
|- data #数据
|- data1.txt
.
.
.
|- data10.txt
|- decoded #解密后的文件
|- encoded #加密后的文件
|- inc #头文件
|- des.h
|- cmd.h
|- src #源文件
|- des.c
|- cmd.c
|- main.c
|- des.exe #des程序
|- log.txt #日志文件
|- makefile #makefile
|- demo.mp4 #演示视频
|- ui.py #图像界面脚本
-
bit级别操作
因为明文是64bit一组,故采用了
unsigned long long来存储一组明文,对下标置换、移位等操作用到了bit级的c语言代码: -
Des计算单元
-
CBC模式
-
5种DES算法
- DES-EEE3
- DES-EDE3
- DES-EEE2 (
$K1=K3$ ) - DES-EDE2 (
$K1=K3$ )
-
用户界面——命令行操作
-
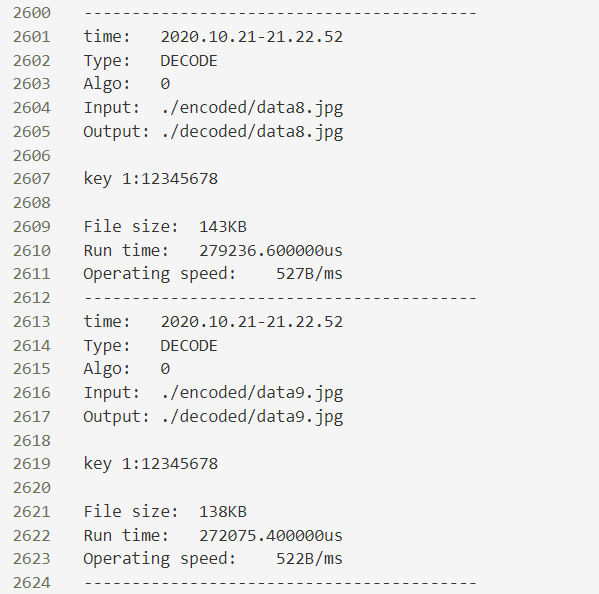
打印日志
加/密时间, 密钥, 输入/除路径等信息,类似如下:
-
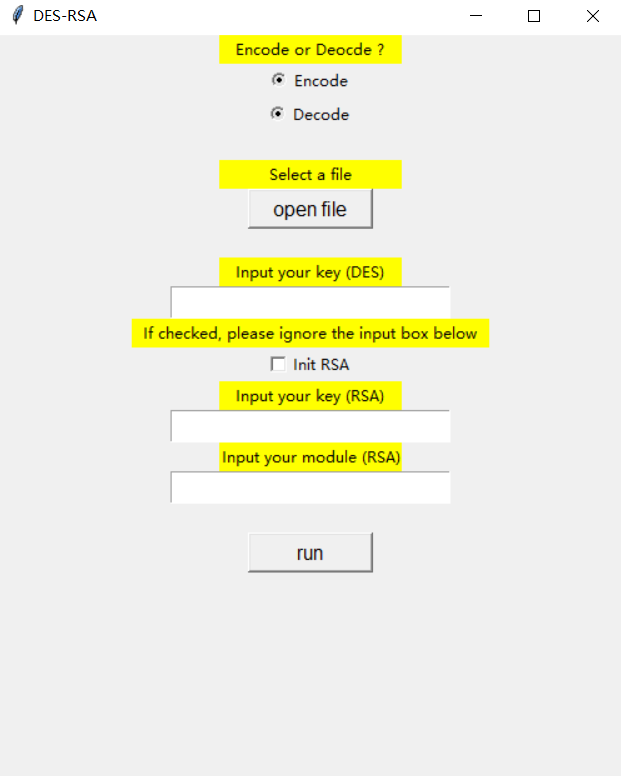
图形界面,利用pyhton的tkinter模块构建简单的用户界面获取参数,然后把参数组织成命令行形式,通过
os.system('cmd')输入命令行,调用des.exe程序进行批量加解密。该python程序只是用来获取用户选择的参数,模拟命令行操作,所以必须依赖于
des.exe才能使用
- 效果良好,可以一般文件进行加解密,程序中设置了
#define MAX_BUFF_SIZE 1024*1024*10即最大支持文件大小为10MB。对一般的.txt、.jpg、.mp4等文件,实验结果良好。 - 速度理想。实验过程中稳定在500B/ms(考虑到硬件条件,不同机器速度会不一样,小文件略快(<1MB)。
**待改进:**对密钥和明文的输入局限于以字节为单位,未实现01的比特序列的输入接口。
**安全性:**56位的密钥(64位中有8位作为校验位)共有$2^{56}$种可能,大约是$7.2\times10^{16}$。对于今天的系统,多台机器同时工作,蛮力破解DES是可行的。但我们可以通过增加密钥长度,和加密次数来增强加密的结果。如把密钥长从64-bit增加至128-bit。所需蛮力破解的时间就会变为原来的$2^{64}$倍,如果原来破解需要1小时,那么现在可能就需要$10^{17}$年!3重DES就是通过多次加密来达到足够的安全性。
《计算机安全》第5章
tkinter — Python interface to Tcl/Tk
本次PJ实现如下内容:
-
DES的UI界面(ui.py)输入由8位字符串改为了十进制数字($0\sim2^{64}-1$)
-
RSA模块
- 生成RSA密钥对
- 可对输入数据加/解密
- 可对输入文件加/解密
-
DES-RSA捆绑脚本
- DES用来加密文件,RSA用来加密DES密钥,两者最终组合成加密后的文件。
-
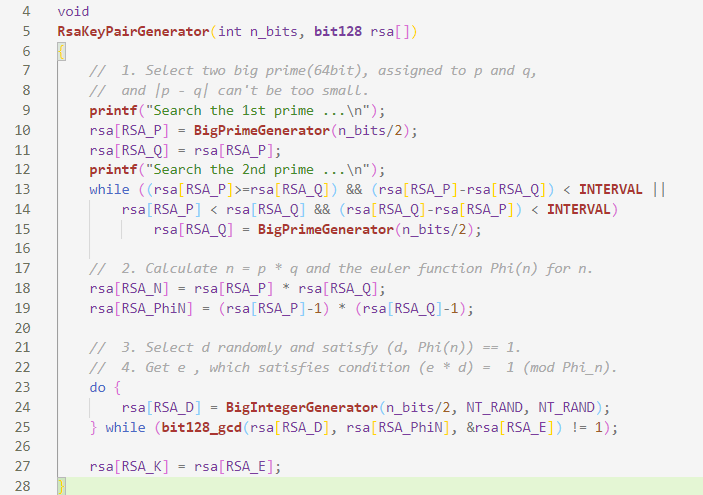
选择两个大素数$p, q$
-
计算$n=p*q,\ \ \ \phi(n)=(p-q))(q-1)$
-
随机选取整数$d$作为私钥,满足$(d,\phi(n))=1$
-
计算公钥$e$,使其满足$e*d = 1 mod\ \phi(n)$
加密:
解密: $$ m = c^d mod\ n $$
-
使用RSA加密一个整数($0\sim2^{128}-1$),使用如下命令(演示见
.\rsa\demo-rsa.mp4)$ cd rsa # 进入.\rsa\目录下,确保可执行文件rsa.exe已经存在,如果不存在,可运行 $ make 编译运行生成rsa.exe $ rsa.exe -d 待加密的数字 --init # 初始化一个RSA密钥对并使用该密钥对对输入数字(2~37位十进制整数,即在128bit的表示范围内)进行加密
如果已经有RSA密钥对可执行以下命令进行加密:
$ cd rsa $ rsa.exe -d 待加密的数字 -p 你的公钥 -m 你的模数解密命令:
$ cd rsa $ rsa.exe -d 加密的结果 -s 你的密钥 -m 你的模数 -
图形界面操作:(演示见
demo-des-rsa.mp4)
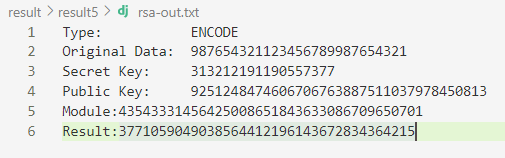
.result5\out\目录下保存 了加密后的文件。
使用DES-RSA组合加密文件,RSA用来加密DES密钥,DES用来加密文件。把DES密钥的加密结果高位补零的方式填充至40位十进制数字,按照字符形式存储在加密文件首部,RSA模数填充至40位紧跟在加密后的DES密钥之后,然后是使用DES加密后的数据。(如下图) 。传输时,只需要把
out\文件夹传给拥有私钥的用户即可。这里为了方便测试,直接使用了初始化的RSA密钥encoded des key][rsa module][encoded data] |-----40B------|----40B-----|--variable--|
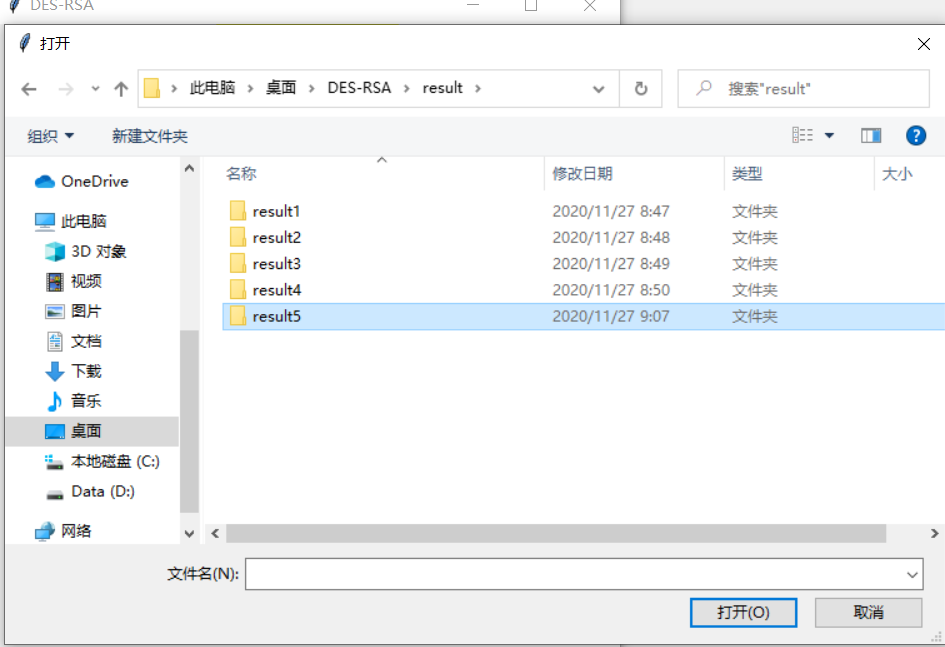
- 选择
Decode, 选择待解密的文件,只需要输入RSA私钥,点击run
- 查看解密结果,解密成功!
- 总结:加密需要DES密钥、RSA公钥和RSA模数(或者init); 解密只需要RSA私钥
-
环境工具
- 操作系统: Win10-64bit
- 编译器:**gcc version 8.1.0 **
- 编程语言: C、Python
-
Github:
-
文件结构
DES-RSA |- data #测试数据 |- data1.txt ... |- data10.txt |- des |- decoded #DES解密后的文件 |- encoded #DES加密后的文件 |- inc #DES头文件 |- des.h |- cmd.h |- src #DES源文件 |- des.c |- cmd.c |- main.c |- des.exe #des程序 |- des-log.txt #DES日志文件 |- makefile |- ui.py #DES图像界面脚本 |- rsa |- key #保存RSA生成的密钥对 |- out #RSA加密后的文件 |- inc #RSA头文件 |- cmd.h |- macro.h |- prime.h |- rsa.h |- src #RSA源文件 |- cmd.c |- main.c |- prime.c |- rsa.c |- rsa.exe #rsa程序 |- rsa-log.txt #RSA日志文件 |- makefile |- demo-rsa.mp4 #RSA演示视频 |- des-rsa.py #DES-RSA图像界面脚本 |- README.md -
C语言大整数运算代码说明
不同于DES的置换操作,RSA涉及到大整数的加减乘除以及求幂取模运算。采用
_uint128_t作为128bit大整数的存储类型,并采取以下几点做法来避免运算的溢出:-
对可能的减法溢出(产生负数),采用额外的变量
sign_x来维护大整数x的符号。(写代码过程中只有很小的一部分涉及减法运算) -
对可能加法溢出,如
(a+b) % n, 采用a + b - p的方式取模 -
对可能的乘法溢出,如
(a * b)% n,采用二分法的方式,拆解为(a * (b/2) + a * (b/2)) % p(假设b是偶数, 奇数类似处理),对其进行$\lceil log_2b\rceil $次加法运算来实现。 -
对可能的求幂溢出, 如
pow(a ,b) % n,采用二分法的方式,拆解为pow(a, b/2) * pow(a, b/2) % n(假设b是偶数,奇数类似处理),对其进行$\lceil log_2b\rceil$次乘法运算来实现。乘法再按照3.中的方法分解为加法运算。总共需要$\lceil log_2b\rceil * \lceil log_2a\rceil $次加法 -
对于128位的明文
m大于模数n的情况,通过加密-解密之后,并不会还原到原来的m,而是m % p:
- 考虑到要求是RSA用于对64bit的密钥进行加密,远小于模数(模数一般大于$2^{127}$)实际应用不会出现这种情况。
-
-
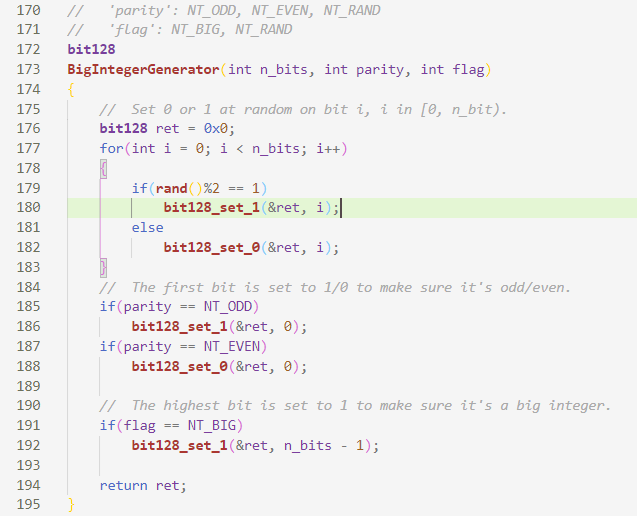
核心代码
-
Win10 64位操作系统 、处理器i5-8300H 23.0GHz, RAM 16GB 的机器上的结果:每个产生一个密钥对大约花费1.1545 毫秒。每执行一次加密-解密 需要4.3286毫秒
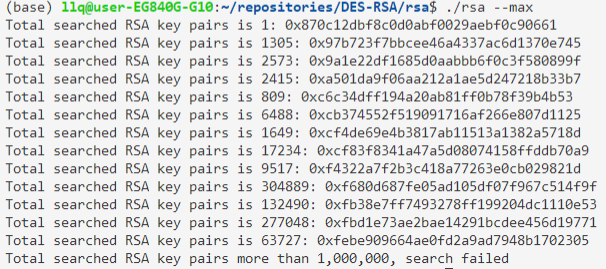
运行
$ cd rsa $ rsa.exe --test结果:
运行
$ cd rsa
$ rsa.exe --speed 结果:
RSA算法中涉及了大量的加法、乘法运算和DES的置换操作相比速度显著地更慢。但RSA理论上的计算困难性以及具有公钥体制的优点,相比之下,RSA有DES无法替代的优点。因此RSA适合和DES组合构成密码系统:RSA用来加密数据量小的DES密钥,DES用来加密原始数据,可以使得密码系统更安全,速度更快。