When it comes to computational chemistry calculations, DFT level of theory provides a reasonable approximation for computing barrier heights (activation energies). Nevertheless, DFT scales . On the other hand, the semi-empirical level of theory provides substantially worse results, but they are computationally much cheaper. Then, it would be interesting to obtain a method that leverages the semi-empirical calculation into DFT level. Our approach consists on using the cheap calculation provided by semi-empirical methods as input for a machine learning model. This can be interpreted as a correction for the semi-empirical level.
The data used for the quantum chemical computations derives from the following levels of theory:
- DFT: the DFT functional used as gold-standard in this case is ωB97X-D3.
- Semi-empirical: the calculations were perfomed at PM7 level of theory with MOPAC.
The data included in this repository includes:
- train_df: Includes the dataset used for training the models, consisting of all the descriptors and the target variables. The validation set should be obtained as a subset of this file.
- test_set: hold-out test set.
- smiles_db: smiles of the entities (reactant, transition state and product) that participate in the reaction.
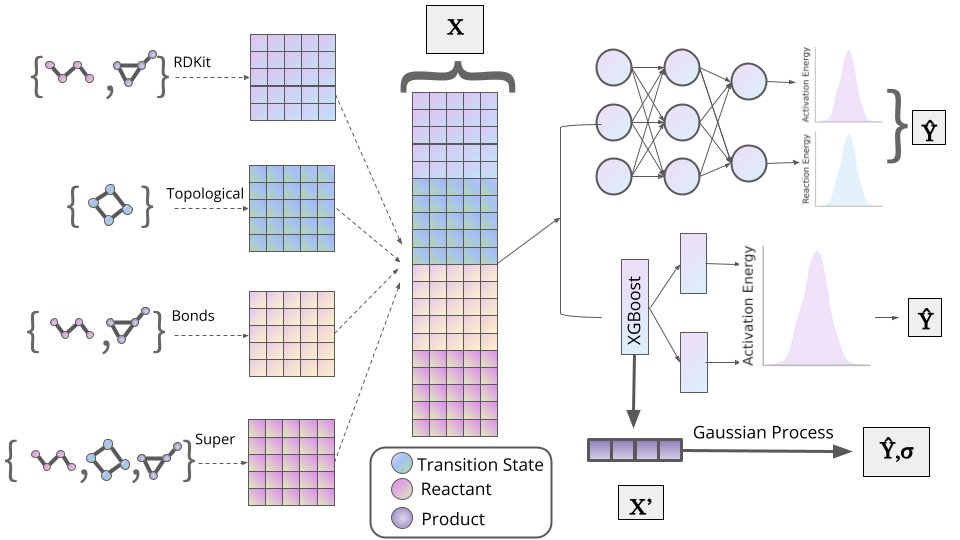
The picture above outlines the procedure followed for this work. The different sets of descriptors are concatenated to use as input for the models that we considered. In the case of the Deep Learning solution, the target variables are not only the barrier height, but also the reaction entalphy, trained in a multi-task setting. Then for the gradient boosting learner, only the barrier height is predicted, achieving the highest performance in terms of MAE (mean absolute error). Based on domain knowledge and the predictions mades by the gradient boosting learner, we selected the most important descriptors to be used as input for a Gaussian Process. In this case, we can use a reduced dimensionality as input space and obtain a notion of uncertainty with this model.
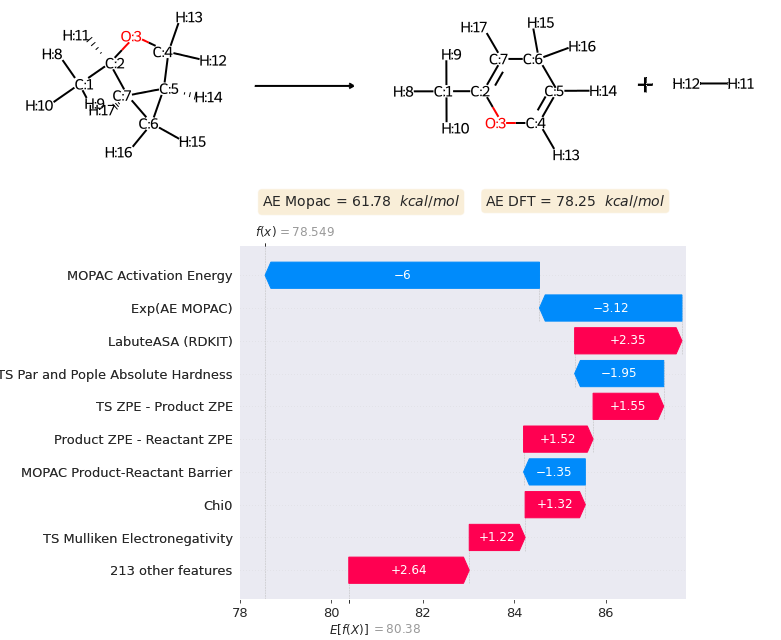
Apart from the raw prediction, this formulation also provides a framework for interpretation of the importance for each descriptor given the model output for a given reaction. The figure below showcases how to interpret the model performance for a ring rearrangement reaction.