livius

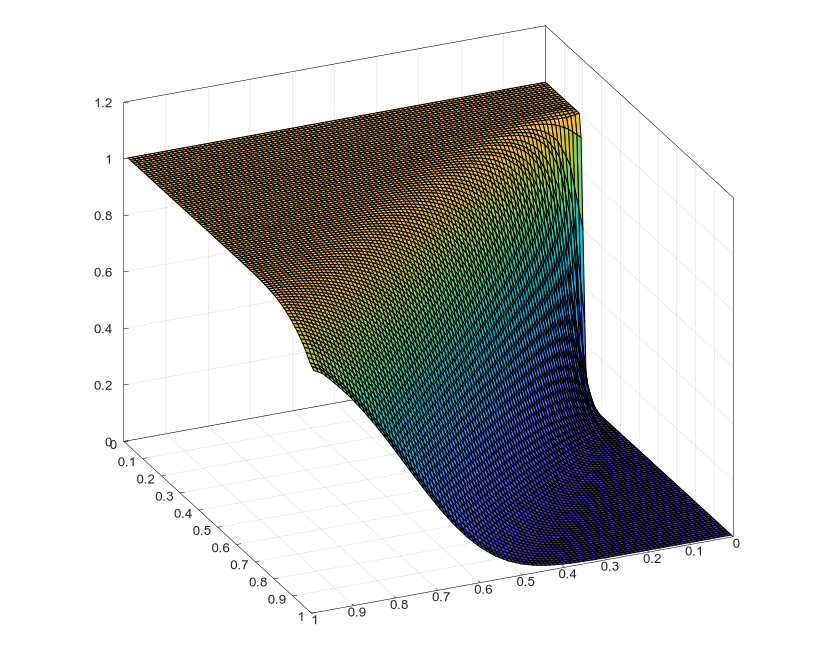
Implementation of various finite element methods such as the discontinuous Galerkin method, the multiscale FEM, SUPG, and the classic FEM. The implementation includes working with 2D meshes (high-order triangular and rectangular elements) and 3D meshes (tetrahedral and cubical elements).

1D/2D grids can be generated within while for 3D problems Gmsh is used to create tetrahedral meshes. For solving linear systems of equations the library uses Eigen library as well as a built-in one.

To run an eigenvalue convection-diffusion problem

$$a(x)\cdot\nabla u(x) - \nabla\cdot\kappa(x)\nabla u(x) = \lambda u(x), \mspace{15mu}\text{in the unit domain }\mspace{15mu}\Omega=[0,1]$$

with $a(x)=[1,1]$ and $\kappa(x)=1$ using the finite element method with bilinear basis functions on rectangles, you need to construct a mesh and specify the coefficients in a (cpp) file.

The finite element is defined as a triple $\{K, P, \Sigma\}$ where $K$ is a geometric shape of the element, $P$ are shape fuctions and $\Sigma$ are degrees of freedom. Here it corresponds to the following code:

template<class Shape, class ShapeFunction, class DoF, class T>
		class CFiniteElement: public CElement<T>
{...}

solvers::fem_solver<CDiffusionScalar, CRegularMesh, vector<double>> fem;

This will declare a solver for a scalar problem on a rectangular mesh. The last parameter corresponds to the type of the solution, i.e. vector means that the solution is stored in a array of doubles.

CRegularMesh mesh{ Point{0,0}, Point{1,1}, 32, 32 };

This will create a mesh with 32x32 elements in the unit domain.

vector<double> solution;

Now to declare various parameters for a problem functions in the form func(Element Material, Node Material, Point) are being used.

const auto source = [=](const int el, const int node, const Point& p)
{
	return 0.;
};

const auto diffusion = [&](const int el, const int node, const Point& p)
{
	return 1.;
};

const auto velocity = [&](const int el, const int node, const Point& p)
{
	return Point(1, 1);
};

const auto boundary = [=](const int el, const int node, const Point& p)
{
	if (p.y < 0.2)
		return 1.;
	return 0.;
};

const parameter<double> boundary_lin(boundary);
const parameter<double> src(source);
const parameter<double> kappa(diffusion);
const parameter<Point>  vel(velocityy);
CDiffusionScalar problem;
problem.addTerm(Terms::EFV);
problem.add_parameter(Terms::EFV, 0, src);
problem.addTerm(Terms::IDUV);
problem.add_parameter(Terms::IDUV, 0, vel);
problem.add_parameter(Terms::IDUDV, 0, kappa);
problem.add_boundary_parameter(1, 0, boundary_lin);
problem.add_boundary_parameter(1, 2, boundary_lin);		

Finally, to find the solution the following command is used

fem.solver_eigen(&problem, &mesh, &solution);

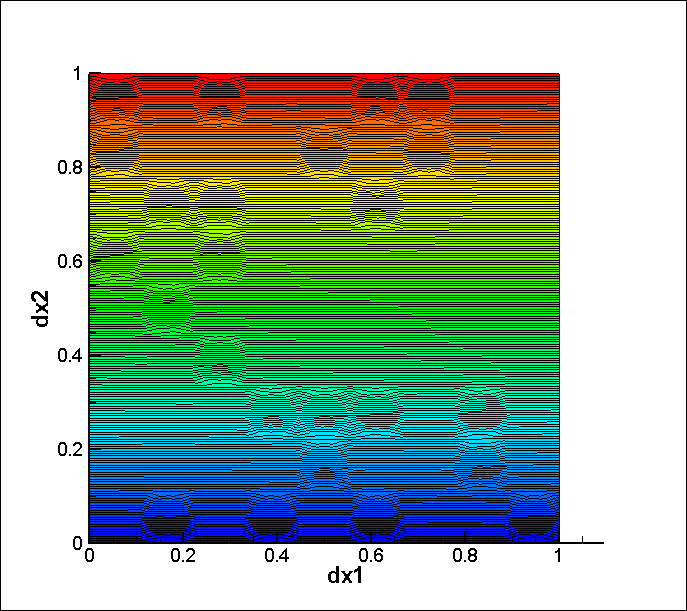
I use Matplot++ to plot the solution

auto [X, Y] = matplot::meshgrid(matplot::iota(0, .01, 1), matplot::iota(0, 0.01, 1));
auto Z = matplot::transform(X, Y, [&](double x, double y) {
	return fem.get_value(mesh, solution, Point(x, y));
});
matplot::surf(X, Y, Z);
//matplot::fcontour(Z)->n_levels(10).filled(true);
matplot::show();

The full code is

#include "../CoreNCFEM/Grids/RegularMesh.h"
#include "../CoreNCFEM/Methods/FEMethod.h"
#include "../Problems/DiffusionScalar.h"
#include "../Solvers/fem_solver.h"
#include <matplot/matplot.h>
#include <random>
#include <math.h>
		
#define _USE_MATH_DEFINES		
		
using namespace corenc;
using namespace Mesh;
using namespace Algebra;
using namespace method;
using MeshType = CRegularMesh;
		
void test()
{
	solvers::fem_solver<CDiffusionScalar, MeshType, vector<double>> fem;
	MeshType mesh{ Point{0,0}, Point{1,1}, 32, 32 };
	std::vector<double> solution;
	const auto source = [=](const int el, const int node, const Point& p)
        {
        	return 0.;
    	};
	const auto diffusion = [&](const int el, const int node, const Point& p)
    	{
        	return 1.;
    	};
	const auto velocity = [&](const int el, const int node, const Point& p)
    	{
        	return Point(1, 1);
    	};
	const auto boundary = [=](const int el, const int node, const Point& p)
    	{
        	if (p.y < 0.2)
            		return 1.;
		return 0.;
    	};
	const parameter<double> boundary_lin(boundary);
    	const parameter<double> src(source);
    	const parameter<double> kappa(diffusion);
    	const parameter<Point>  vel(velocityy);
	CDiffusionScalar problem;
	problem.addTerm(Terms::EFV);
	problem.add_parameter(Terms::EFV, 0, src);
	problem.addTerm(Terms::IDUV);
	problem.add_parameter(Terms::IDUV, 0, vel);
	problem.add_parameter(Terms::IDUDV, 0, kappa);
	problem.add_boundary_parameter(1, 0, boundary_lin);
	problem.add_boundary_parameter(1, 2, boundary_lin);
	fem.solver_eigen(&problem, &mesh, &solution);

	auto [X, Y] = matplot::meshgrid(matplot::iota(0, .01, 1), matplot::iota(0, 0.01, 1));
    	auto Z = matplot::transform(X, Y, [&](double x, double y) {
        	return fem.get_value(mesh, solution, Point(x, y));
    	});
    	matplot::surf(X, Y, Z);
    	//matplot::fcontour(Z)->n_levels(10).filled(true);
    	matplot::show();
}

Gallery

Developer

Stanislav Y. Polishchuk, stanislav_py at proton.me.