Market Simulator

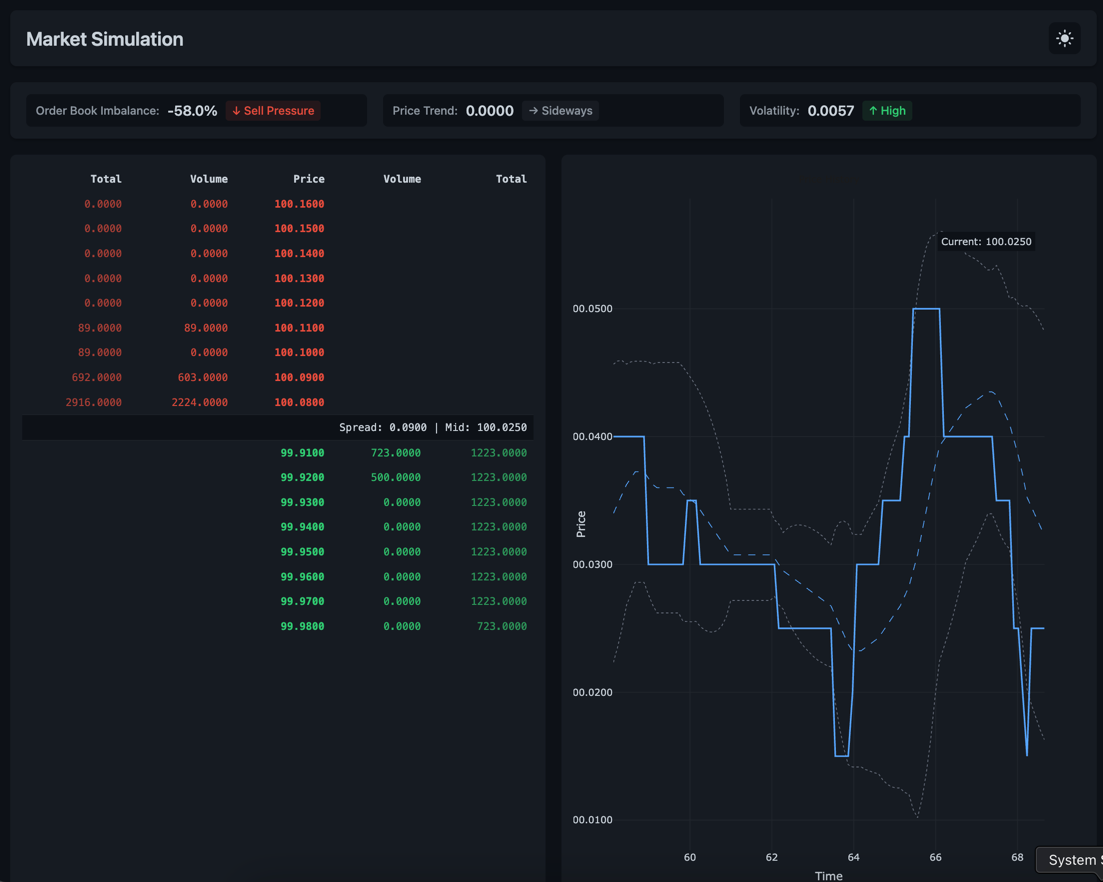
A real-time market simulation system that emulates an order book with price discovery, trend analysis, and live visualization.

Architecture

graph TD
    subgraph Backend
        MS[Market Simulator] --> |Updates| OB[Order Book]
        OB --> |Price/Volume Data| TS[Time Series]
        TS --> |Calculates| T[Technical Indicators]
        T --> |Bollinger Bands| WS[WebSocket Server]
        T --> |Moving Averages| WS
        OB --> |Order Book State| WS
    end

    subgraph Frontend
        WS --> |Real-time Data| UI[Web UI]
        UI --> |Renders| C1[Price Chart]
        UI --> |Renders| C2[Order Book View]
        UI --> |Renders| C3[Market Signals]
    end

Loading

Components

1. Market Simulator (script.py)

• Generates realistic market behavior using a stochastic process
• Simulates order flow with varying volumes and prices
• Implements mean-reversion and momentum regimes
• Key parameters:
  • Price volatility
  • Order arrival rate
  • Volume distribution
  • Price impact factors

2. Order Book

• Maintains bid and ask price levels
• Tracks volume at each price level
• Calculates market metrics:
  • Best bid/ask prices
  • Order book imbalance
  • Price levels and volumes
• Implements price-time priority matching

3. Technical Analysis

• Real-time calculation of indicators:
  • Simple Moving Average (20-period)
  • Bollinger Bands (2 standard deviations)
  • Price trend detection
  • Volatility measurement

4. FastAPI Server (server.py)

• WebSocket endpoint for real-time data streaming
• Serves static files for web interface
• Manages client connections
• Broadcasts market updates to all connected clients

5. Web Interface (static/index.html)

• Interactive price chart using Plotly.js
• DOM-based order book visualization
• Real-time market signals:
  • Order book imbalance
  • Price trend
  • Volatility regime
• Dark/Light theme support

Data Flow

1. Market Simulator generates orders
2. Orders update the order book state
3. Technical indicators are calculated from price history
4. Server broadcasts updates via WebSocket
5. Web UI receives and visualizes the data

Technical Stack

• Backend:

  • Python 3.8+
  • FastAPI for WebSocket server
  • NumPy for numerical computations
  • Uvicorn for ASGI server

• Frontend:

  • HTML5/CSS3
  • JavaScript (Vanilla)
  • Plotly.js for charting
  • CSS Variables for theming

Running the Simulator

1. Install dependencies:

pip install fastapi uvicorn numpy

2. Start the server:

python server.py

3. Open in browser:

http://localhost:8000

Implementation Details

Price Generation

The simulator uses a mean-reverting random walk with momentum factors:

• Base price follows Ornstein-Uhlenbeck process
• Momentum overlay adds trending behavior
• Volume generation follows power law distribution
• Order placement uses realistic spread distribution

Order Book Implementation

• Price levels stored in sorted dictionaries
• O(1) lookup for price level volumes
• O(log n) insertion and removal of orders
• Efficient volume aggregation at price levels

Technical Analysis

• Moving averages use rolling window
• Bollinger Bands dynamically adjust to volatility
• Trend detection uses exponential weighting
• Volatility calculated with Parkinson estimator

WebSocket Protocol

Messages follow this structure:

{
  "timestamps": [...],
  "mid_prices": [...],
  "price_levels": [...],
  "bid_volumes": {...},
  "ask_volumes": {...},
  "best_bid": float,
  "best_ask": float,
  "signals": {
    "imbalance": [...],
    "trend": [...],
    "volatility": [...]
  },
  "trends": {
    "sma": [...],
    "upper_band": [...],
    "lower_band": [...]
  }
}

Market Simulator Details

Price Process

The market simulator implements a sophisticated price generation process that combines several stochastic elements:

1. Base Price Process (Ornstein-Uhlenbeck) The core price process follows an Ornstein-Uhlenbeck mean-reverting model:

   dP(t) = θ(μ - P(t))dt + σdW(t)
   

   where:

   • P(t) is the price at time t
   • θ is the mean reversion speed
   • μ is the long-term mean price
   • σ is the volatility parameter
   • W(t) is a Wiener process (Brownian motion)

2. Momentum Overlay A momentum factor is added to capture trending behavior:

   M(t) = α * ΣP(t-i)Δt * exp(-λi)
   

   where:

   • α is the momentum coefficient
   • λ is the decay factor
   • Δt is the time step

3. Final Price Process The combined price process becomes:

   P_final(t) = P(t) + M(t) + J(t)
   

   where J(t) is a jump process for sudden price movements:

   J(t) = N(t) * Y(t)
   

   • N(t) is a Poisson process for jump timing
   • Y(t) is normally distributed jump size

Order Generation

1. Volume Distribution Order sizes follow a power law distribution:

   P(V > x) ∝ x^(-α)
   

   where α ≈ 1.5 (empirically observed in real markets)

2. Order Arrival The arrival of orders follows a Poisson process with varying intensity:

   λ(t) = λ₀ * (1 + β * |r(t)|)
   

   where:

   • λ₀ is the base arrival rate
   • β is the sensitivity to returns
   • r(t) is the recent return

3. Price Level Selection Order placement follows a Student's t-distribution around the current price:

   ΔP ~ t(ν) * σ_spread
   

   where:

   • ν is the degrees of freedom (typically 3-5)
   • σ_spread is the base spread width

Market Microstructure

1. Order Book Imbalance Calculated as normalized volume difference:

   I(t) = (V_bid - V_ask) / (V_bid + V_ask)
   

   where V_bid and V_ask are total volumes at best levels

2. Price Impact Market impact follows a square-root law:

   ΔP ∝ sign(V) * √|V|
   

   where V is the order volume

3. Volatility Regime Local volatility is estimated using the Parkinson high-low estimator:

   σ²(t) = (ln(H/L))² / (4ln(2))
   

   where H and L are local high and low prices

Technical Indicators

1. Simple Moving Average (SMA)

   SMA(t) = (1/n) * Σ P(t-i) for i=0 to n-1
   

2. Bollinger Bands

   Upper(t) = SMA(t) + k * σ(t)
   Lower(t) = SMA(t) - k * σ(t)
   

   where:

   • k is typically 2 (2 standard deviations)
   • σ(t) is rolling standard deviation

3. Trend Detection Using exponential regression:

   β = Σ(t - t̄)(P(t) - P̄) / Σ(t - t̄)²
   

   where β is the trend coefficient

Implementation Notes

1. Numerical Integration The stochastic differential equations are solved using the Euler-Maruyama method:

   P(t+Δt) = P(t) + θ(μ - P(t))Δt + σ√(Δt)Z
   

   where Z ~ N(0,1)

2. Parameter Calibration Key parameters are calibrated to match stylized facts of real markets:

   • Fat-tailed returns (kurtosis > 3)
   • Volatility clustering
   • Mean reversion at short timescales
   • Momentum at medium timescales

3. Efficiency Considerations

   • Price updates: O(1)
   • Order book updates: O(log n)
   • Technical indicator updates: O(1) using rolling windows
   • Memory usage: O(n) where n is the number of price levels

Market Regimes

The simulator can operate in different regimes:

1. Mean-Reverting Market

   • High θ (mean reversion speed)
   • Low momentum coefficient
   • Narrow spread distribution

2. Trending Market

   • Low θ
   • High momentum coefficient
   • Higher volatility

3. Volatile Market

   • High jump intensity
   • Wide spread distribution
   • High order arrival rate

4. Calm Market

   • Low volatility
   • Tight spreads
   • Balanced order flow

Each regime can be activated by adjusting the corresponding parameters in the configuration.

Screenshots

Future Improvements

1. Add more technical indicators:

   • RSI, MACD, Volume Profile
   • Order flow imbalance
   • Price impact estimation

2. Enhanced visualization:

   • Depth chart view
   • Time and sales
   • Heat map visualization

3. Market making simulation:

   • Automated trading strategies
   • Liquidity provision
   • Market impact analysis

4. Performance optimizations:

   • Binary protocol for WebSocket
   • Efficient data structures
   • Batch updates

Contributing

Feel free to submit issues and enhancement requests!