C++ Data Structures and Algorithms

Read this in other languages: 🇨🇳简体中文

This repository contains C++ based examples of many popular algorithms and data structures.

Each algorithm and data structure has its own separate README with related explanations and links for further reading.

☝ Note that this project is meant to be used for learning and researching purposes only, and it is not meant to be used for production.

Data Structures

A data structure is a particular way of organizing and storing data in a computer so that it can be accessed and modified efficiently. More precisely, a data structure is a collection of data values, the relationships among them, and the functions or operations that can be applied to the data.

Remember that each data has its own trade-offs. And you need to pay attention more to why you're choosing a certain data structure than to how to implement it.

B - Beginner, A - Advanced

• B Array
  • B Static Array
  • B Dynamic Array
  • B String
• B Linked List
  • B Singly Linked List
  • B Doubly Linked List
• B Queue
• B Stack
• B Hash Table

Algorithms

An algorithm is an unambiguous specification of how to solve a class of problems. It is a set of rules that precisely define a sequence of operations.

B - Beginner, A - Advanced

How to Use This Repository

Every directorys under /data-structures or /algorithms should be treated as a independent project. For example, the LinkedList under data-structures has this structure:

.
├── assets
│   └── linkedlist.jpg
├── build.sh
├── clean.sh
├── CMakeLists.txt
├── include
│   └── LinkedList.h
├── README.md
├── src
│   └── LinkedList.cpp
└── __test__
    └── test_LinkedList.cpp

Useful Infomation

Big O Notation

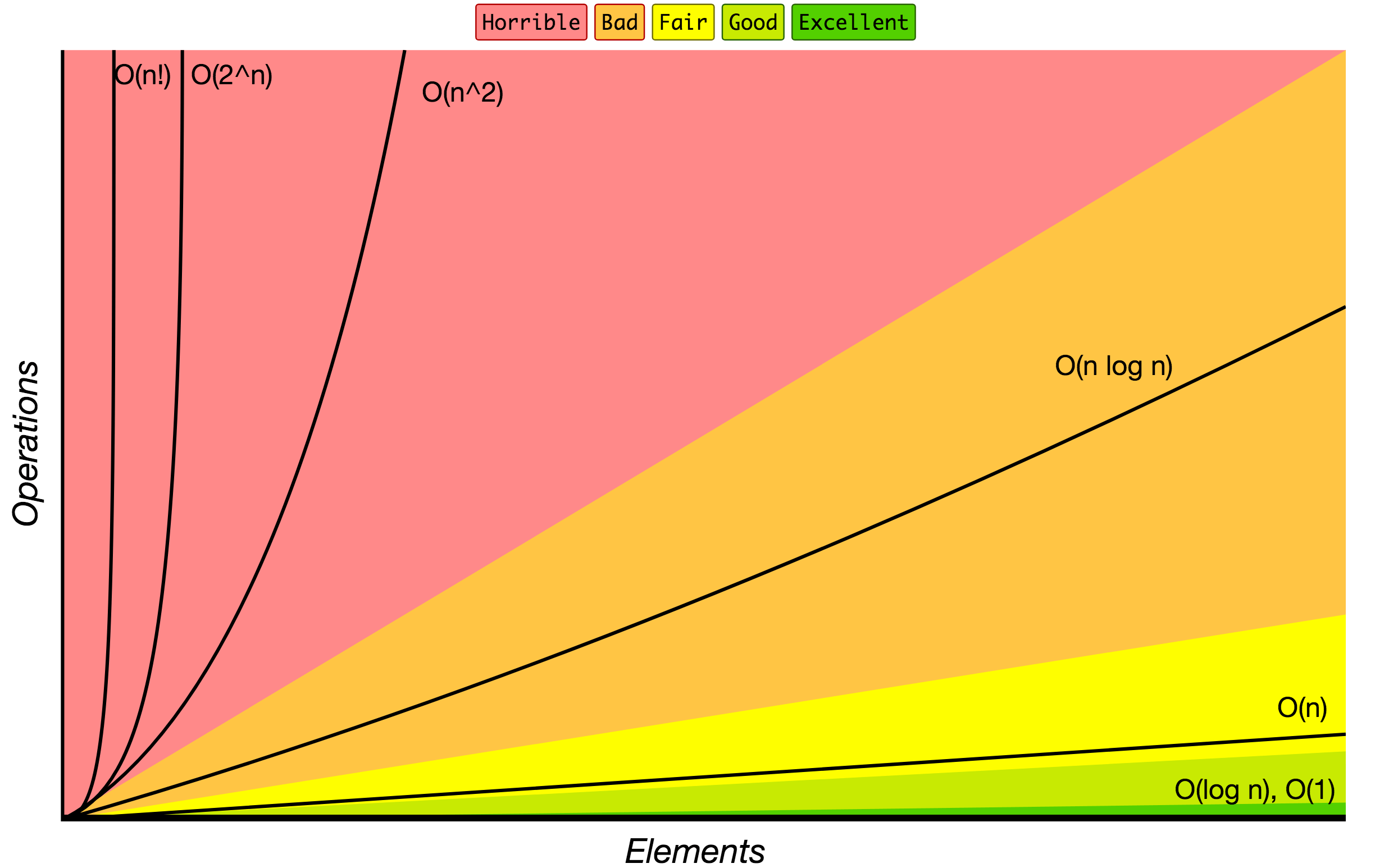
Big O notation is used to classify algorithms according to how their running time or space requirements grow as the input size grows. On the chart below you may find most common orders of growth of algorithms specified in Big O notation.

Source: Big O Cheat Sheet.

Below is the list of some of the most used Big O notations and their performance comparisons against different sizes of the input data.

Big O Notation	Type	Computations for 10 elements	Computations for 100 elements	Computations for 1000 elements
O(1)	Constant	1	1	1
O(log N)	Logarithmic	3	6	9
O(N)	Linear	10	100	1000
O(N log N)	n log(n)	30	600	9000
O(N^2)	Quadratic	100	10000	1000000
O(2^N)	Exponential	1024	1.26e+29	1.07e+301
O(N!)	Factorial	3628800	9.3e+157	4.02e+2567

Data Structure Operations Complexity

Data Structure	Access	Search	Insertion	Deletion	Comments
Array	1	n	n	n
Stack	n	n	1	1
Queue	n	n	1	1
Linked List	n	n	1	n
Hash Table	-	n	n	n	In case of perfect hash function costs would be O(1)
Binary Search Tree	n	n	n	n	In case of balanced tree costs would be O(log(n))
B-Tree	log(n)	log(n)	log(n)	log(n)
Red-Black Tree	log(n)	log(n)	log(n)	log(n)
AVL Tree	log(n)	log(n)	log(n)	log(n)
Bloom Filter	-	1	1	-	False positives are possible while searching

Array Sorting Algorithms Complexity

Name	Best	Average	Worst	Memory	Stable	Comments
Bubble sort	n	n2	n2	1	Yes
Insertion sort	n	n2	n2	1	Yes
Selection sort	n2	n2	n2	1	No
Heap sort	n log(n)	n log(n)	n log(n)	1	No
Merge sort	n log(n)	n log(n)	n log(n)	n	Yes
Quick sort	n log(n)	n log(n)	n2	log(n)	No	Quicksort is usually done in-place with O(log(n)) stack space
Shell sort	n log(n)	depends on gap sequence	n (log(n))2	1	No
Counting sort	n + r	n + r	n + r	n + r	Yes	r - biggest number in array
Radix sort	n * k	n * k	n * k	n + k	Yes	k - length of longest key

Star History

References

1. trekhleb's javascript-algorithms