The UrbanGB dataset

Contents, format and licence

The file "urbanGB.zip" contains three files: "urbanGB.txt", "urbanGB.labels.txt" and "urbanGB.centr.txt".

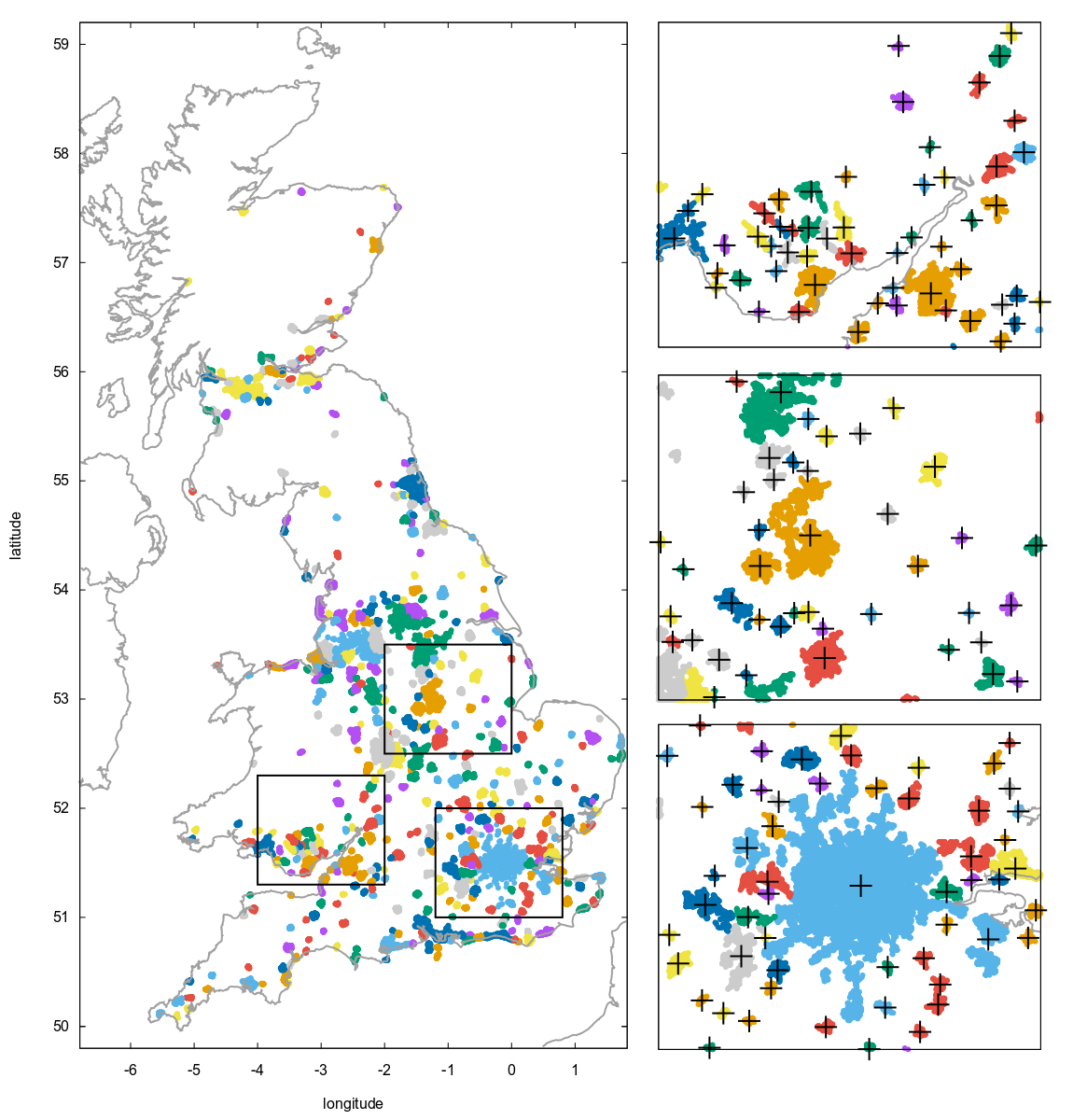
The data in "urbanGB.txt" consists of the coordinates (longitude and latitude) of road accidents within Great Britain urban areas. Its size is 360177×2.

This data was originally downloaded from this Kaggle page, and subsequently filtered to include only the accidents categorized as "urban". All the columns except for the coordinates were then removed. Some data points that could not be associated to a sufficiently large urban center were also discarded (see below for more details).

The license for this data is the Open Government Licence used by all data on data.gov.uk. The raw datasets are available from the UK Department of Transport website here.

The file "urbanGB.labels.txt" contains a labelling of the points that roughly reflects their partitioning in urban centers, in numeric format: each row contains a label between 1 and 469 associated to the corresponding datum in "urbanGB.txt". The procedure used to obtain this partitioning is explained below.

The file "urbanGB.centr.txt" contains the coordinates of the 469 barycenters ("centroids") of each partition.

The size of each partition ranges from a minimum of 20 to a maximum of 84524.

This partition and centroid data is made available under the Open Database License.

Purpose and usage

The partitioning in urban centers is approximate, it is intended as an integration of both geometrical and administrative features. In short, the points were first divided in small units according to their topological name, then the units were aggregated based on geometrical proximity (details below). The purpose is to provide a fairly large, realistic and very challenging test for clustering algorithms such as those of the k-means family (indeed, it was expressly created to test the recombinator-k-means algorithm).

Since the data is provided in coordinates format, in order to compute geographical distances between the points one would need to account for the curvature of the Earth. For this dataset, scaling down the first coordinate (longitude) by a factor of 1.7 is sufficient to ensure that Euclidean distances computed on the dataset are approximately proportional to geographical ones.

Details on the construction of the dataset labels

This is the procedure used to generate the labels in "urbanGB.labels.txt".

First, each coordinate point was reverse-geolocalized through the Open Street Map server, collecting the following information (if present): region, county, city, town, village, suburb, hamlet. These were used to create a tag for each point. The primary tagging mode was by using the suburb information if present, qualified with the hamlet/village/town/city name (if present), the county and the region. The snippet of Julia code used to construct the tag variable is this (note that the region was always present, and that some data entries were skipped at this level):

qualifier = "rg=$region"
qlst = [hamlet, village, town, city]
qfst = findfirst(x->x ≠ "?", qlst)
if qfst ≡ nothing
    if county == "?" || suburb == "?"
        continue # skip the entry entirely
    else
        tag = "$suburb [$county] $qualifier"
    end
else
    cq = qlst[qfst]
    if suburb == "?"
        tag = "$cq [$county] $qualifier"
    else
        county ≠ "?" && (qualifier = "cn=$county $qualifier")
        tag = "$suburb [$cq] $qualifier"
    end
end

The points were partitioned according to their tags. Then, an agglomeration phase was performed. The single-linkage distance between each pair of partitions was computed, and the partitions were sorted in decreasing order according to their size. We set two size thresholds, Tmin=20 and Tmax=5000, and a distance threshold eps=0.01, and performed the following iterative step:

• Consider the smallest partition that has not been marked as "ignored" yet.

  • If its size is larger or equal than Tmax, stop the iteration (we're done).

  • If its closest partition is at a distance smaller or equal than eps, merge them, update the distances and the rankings and restart the iteration

  • If its size is less then Tmin, remove the partition entirely

  • Otherwise, mark the partition as "ignored" and restart the iteration

In words, this procedure agglomerates the smallest partitions (i.e. the suburbs, originally) into larger urban areas as long as they are contiguous, and up to a certain size; orphaned partitions that are too small are removed.

This procedure creates a few artifacts and it might be refined, but it's generally satisfactory at producing mostly blob-like clusters that reflect the division of the points in urban centers, in a way that resembles what could plausibly be done manually. Of course, since this partition is ultimately based on administrative classifications, no algorithm could ever infer it perfectly from the coordinate data alone.