fem_1d1st

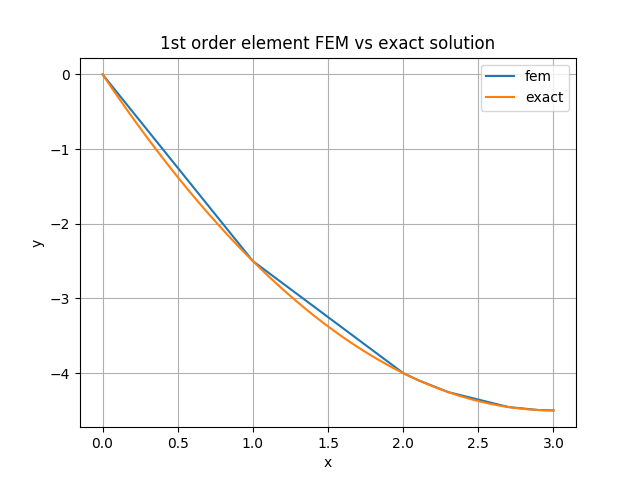
one dimensional first order element finite element method(Galerkin method) using BiCGSTAB method + diagonal preconditioning.

requirements for python:

• numpy
• scipy
• matplotlib
• f90nml

how to test:

$ vi fort.11 # adjust length, this is the right boundary, left boundary is zero
$ vi fort.7  # add values between zero and length
$ make
$ ./a.out
 e%nelements:           7
 e%nnodes:              8
 points:
   0.00000E+00   1.00000E+00   2.00000E+00   2.10000E+00   2.30000E+00   2.70000E+00   2.90000E+00   3.00000E+00
 lhs A:
   1.00000E+00   0.00000E+00   0.00000E+00   0.00000E+00   0.00000E+00   0.00000E+00   0.00000E+00   0.00000E+00
  -1.00000E+00   2.00000E+00  -1.00000E+00   0.00000E+00   0.00000E+00   0.00000E+00   0.00000E+00   0.00000E+00
   0.00000E+00  -1.00000E+00   1.10000E+01  -1.00000E+01   0.00000E+00   0.00000E+00   0.00000E+00   0.00000E+00
   0.00000E+00   0.00000E+00  -1.00000E+01   1.50000E+01  -5.00000E+00   0.00000E+00   0.00000E+00   0.00000E+00
   0.00000E+00   0.00000E+00   0.00000E+00  -5.00000E+00   7.50000E+00  -2.50000E+00   0.00000E+00   0.00000E+00
   0.00000E+00   0.00000E+00   0.00000E+00   0.00000E+00  -2.50000E+00   7.50000E+00  -5.00000E+00   0.00000E+00
   0.00000E+00   0.00000E+00   0.00000E+00   0.00000E+00   0.00000E+00  -5.00000E+00   1.50000E+01  -1.00000E+01
   0.00000E+00   0.00000E+00   0.00000E+00   0.00000E+00   0.00000E+00   0.00000E+00  -1.00000E+01   1.00000E+01

 rhs b:
   0.00000E+00
  -1.00000E+00
  -5.50000E-01
  -1.50000E-01
  -3.00000E-01
  -3.00000E-01
  -1.50000E-01
  -5.00000E-02
 BiCGSTAB method converged.
 iter, res:           6  2.311200543208557E-015
 check passed.

$ ./draw.py
$ display fem.png

TODO:

• do FEM by second order element(ax^2 + bx + c) in 1D
• try 2D, 3D
• parallelize it by MPI

graph