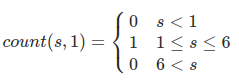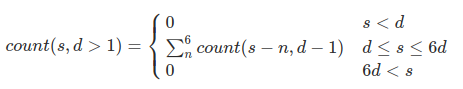Algorithm to solve the "How many configurations of 20 dice sum 70?" problem answered in es.quora.com
We define count(S,D) as "how many configurations of D dice sum S".
This definition can be expressed algebraically as
And can be written as a recursive algorithm:
/// how many configurations of <d> dice sum <s>?
function count(s, d) {
if (s < d || d * 6 < s)
return 0
else if (d === 1)
return 1
else
return [1, 2, 3, 4, 5, 6].fold( (total, side)=>total+count(s - side, d - 1), 0)
}This algorithm, without any optimizacion, has a complexity order of O( D * 6^D ) where D is the number of dice.
The code you can find in this project shows how performance can be improved drastically adding memoization or converting tail recursion to an iterative version.
The evolution is shown with this 4 code files
solution01_no_memoized.js runs the standard algorithm for 2, 4, 5, ..., 12 dice.
solution02_memoized.js runs the memoized version for 2,4,6, ..., 150 dice.
solution03_memoized_with_counters.js runs the memoized version for 2 to 150 dice adding some counters:
- callsCount: How many times "count" function has been called.
- memoizedCount: How many values have been memoized.
solution04_iterative.js runs the iterative version for 2,4,6,..., 150 dices The idea:
-
Iterative solution generates all counts from count(1,1) to count(sum,dices) taking into account that each state count(s,d) depends, at most, on the state count(s-6, d-1).
-
The tail recursion is ported easily to iterative version keeping the record of the previously calculated states into a circular array of 7 rows.
You need nodejs on your system
If you use Ubuntu linux, you can install it with
sudo apt install nodejs
To run tests just do
$ node solution01_no_memoized
or
$ node solution02_memoized
or
$ node solution03_memoized_with_counters
or
$ node solution04_iterative
Anyway, I include results of this 4 executions (performed with my i5) on results folder
We only test 1 sum for each number of dice d: the one with more configurations (the worst case):
s = (d + 6d) / 2
i.e.:
count(14, 5)
14 = (5 + 30) / 2
count(21, 6)
21 = (6 + 35) / 2
count(28, 8)
28 = (8 + 48) / 2
count(35, 10)
35 = (10 + 60) / 2