We present three examples of rdpermute used as a complement to standard RDD or RKD asymptotic tests.
Example 1: RD
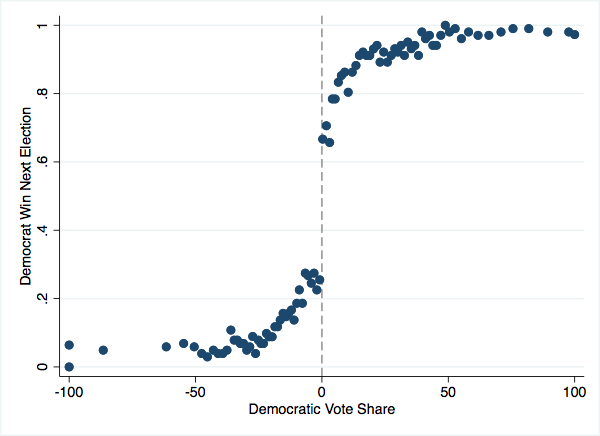
Lee (2008) uses a regression discontinuity design with the vote share margin as the running variable to estimate the effect of incumbency on likelihood of winning the next election. This plot provides visual evidence that a Democrat winning an election discretely increases the probability a Democrat will win the next election.
cap ssc install rdpermute
cap ssc install binscatter
use example_data/lee_election, clear
binscatter y x, line(none) ytitle(Democrat Win Next Election) xtitle(Democratic Vote Share) nquant(100) rd(0)
To conduct the permutation test, we take the data as given and treat the discontinuity point as a random variable. We calculate the RD coefficient at a given set of placebo discontinuities, which are different values of the Democratic vote share. We compare the estimates at these placebos to the estimate at the true discontinuity. We specify the following options:
placebo_disconts(-50(1)49)means we use 100 placebo discontinuities from -50 through 49true_discont(0)means the true discontinuity is at 0deriv_discont(0)means we are looking for a change in the interceptlinearmeans we are using a local linear regression
rdpermute y x, placebo_disconts(-50(1)49) true_discont(0) deriv_discont(0) linear
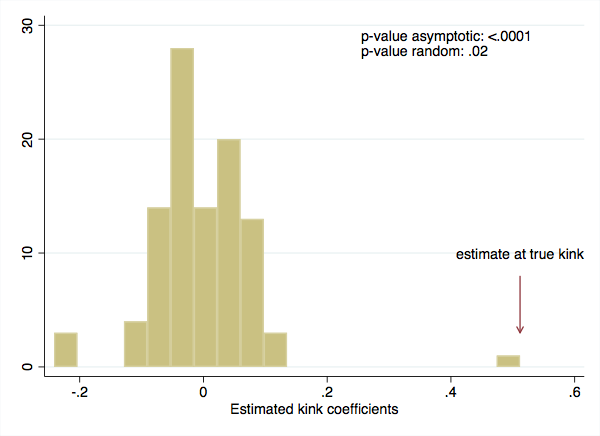
The conclusions from the asymptotic and permutation tests coincide: under both methodologies we reject the null hypothesis that incumbency does not affect future election victory.
Below we plot the placebo distribution with an arrow that points to where the true kink point lies. In this case it is clearly an extreme value in the placebo distribution.
matrix placebos = e(kink_beta_linear)
svmat placebos
local true_beta = placebos[51,1]
twoway hist placebos1 ...
Example 2: RK with kink
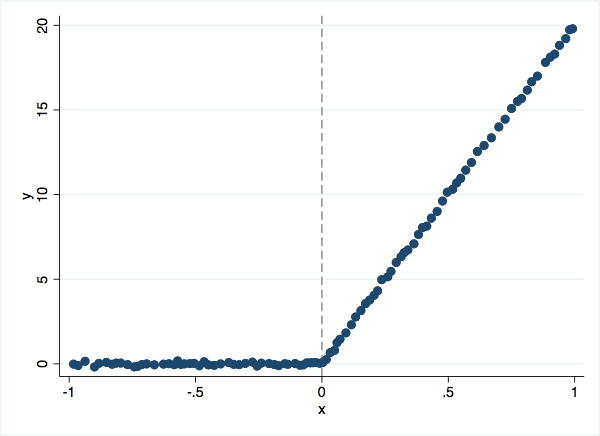
Here we simulate data with an obvious kink at 0.
use "example_data/sim1", clear
binscatter y x, line(none) nquant(100) rd(0)
We specify the following options:
placebo_disconts(-.98(.02)1)means we use 100 placebo kinks from -.98 through 1true_discont(0)means the true discontinuity is at 0linearmeans we are using a local linear regression
The default for deriv_discont(1) means we are looking for a change in the slope.
rdpermute y x, placebo_disconts(-.98(.02)1) true_discont(0) linear
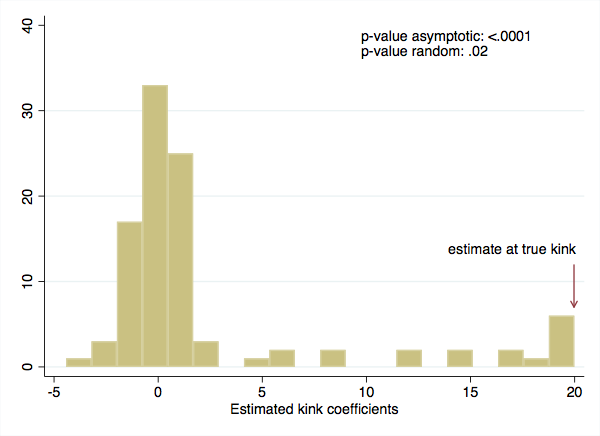
The conclusions from the tests agree: both show highly significant slope changes at the policy kink point.
Once again we plot the placebo distribution with an arrow that points to where the true kink point lies. The true kink point is an extreme value in the placebo distribution. While a few placebo values are within the same histogram bin, the estimated coefficient at the true policy kink point is the most extreme.
matrix placebos = e(kink_beta_linear)
svmat placebos
local true_beta = placebos[51,1]
twoway hist placebos1 ...
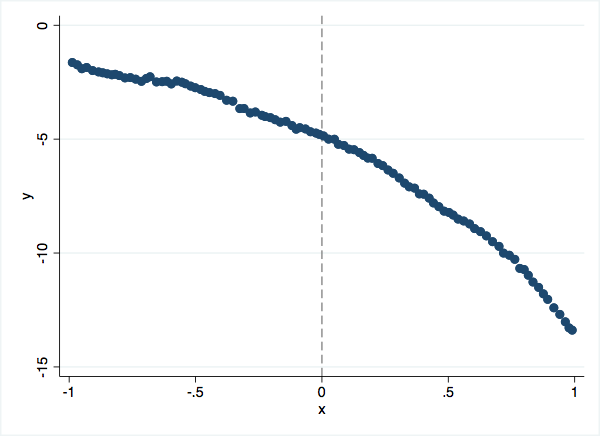
Example 3: RK without kink
In this example, we generate data with curvature around the kink point. In such cases, misspecification of the functional form can lead to spurious RKD coefficients.
use "example_data/sim2", clear
binscatter y x, line(none) nquant(100) rd(0)
We use the same specification as in example 2.
rdpermute y x, placebo_disconts(-.98(.02)1) true_discont(0) linear
The conclusions from the tests disagree. The asymptotic test for linear RKD rejects the null hypothesis even though the underlying data-generating process features no discontinuous slope changes. In contrast, the permutation test correctly detects no kink.
The estimated coefficient at the true policy kink point is near the center of the placebo distribution.
matrix placebos = e(kink_beta_linear)
svmat placebos
local true_beta = placebos[51,1]
twoway hist placebos1 ...
In each example, we used 100 evenly spaced placebos over the main support of the running variable. For an extended discussion of the choice of placebo kink locations, see section 3.3 of Ganong & Jäger (2018).
Citations:
Ganong, P. & Jäger, S. (2018), "A Permutation Test for the Regression Kink Design", Journal of the American Statistical Association, 113:522, 494-504, DOI: 10.1080/01621459.2017.132835
Lee, D. S. (2008), “Randomized Experiments From Non-Random Selection in US House Elections,” Journal of Econometrics, 142, 675–697.