GEMM by CUDA WMMA (tensor core)

本文章介绍的GEMM算法并非最优实现，只是为了介绍CUDA编程和WMMA

GEMM

GEMM 又称为通用矩阵乘，一般为 $$ C=A*B $$

WMMA(tensor core)

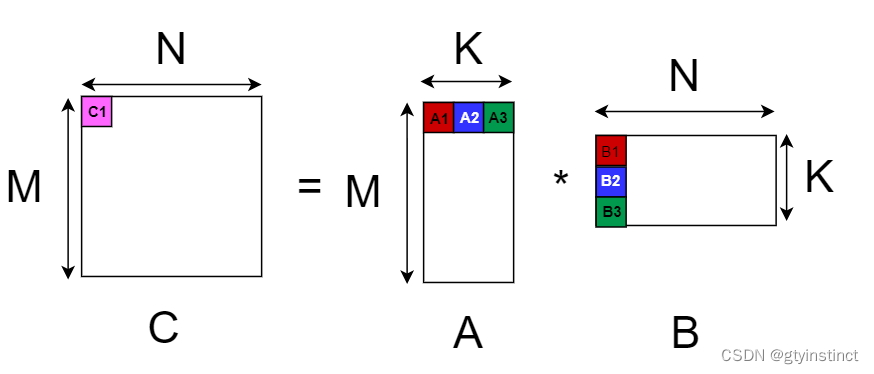
WMMA全称 warp matrix multiply-accumulate，即利用GPU上的tensor core进行warp粒度矩阵乘加速，它通过一个warp内部的线程完成分块的GEMM操作，例如上图中C矩阵的C1分块可以通过A1、A2、A3和B1、B2、B3计算得出，即 $$ C1=A1B1+A2B2+A3B3 $$ 而$A1B1$便可以利用WMMA计算得出

实现思路

WMMA

• 由于WMMA支持的GEMM操作有着固定大小和限制{M_TILE，N_TILE，K_TILE}，所以首先将矩阵{M,N,K}填充至{M_PAD，N_PAD，K_PAD}，填充的值为0，其中

M_PAD = M % M_TILE ? (M/M_TILE+1)*M_TILE : M ;
// N_PAD和K_PAD同理

注意{M,N,K}表示GEMM中A，B，C的维度

• 这样矩阵C,A,B就可以完整地分割成若干个WMMA支持的小矩阵（分块）

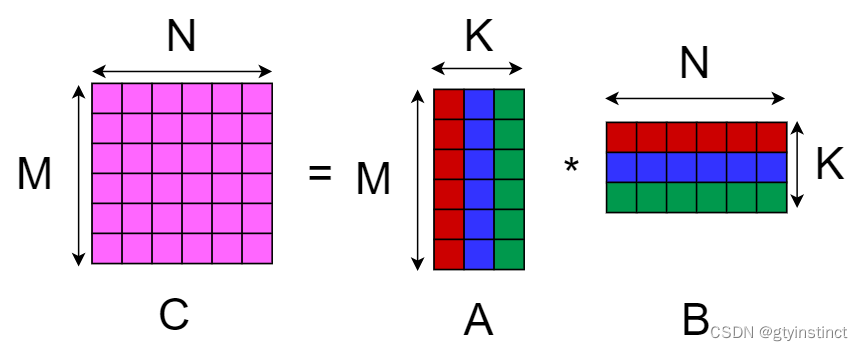
• 矩阵C中的每一个分块索引为(midx,nidx)，均可以由以下公式计算得出 $$ C(midx,nidx)=\sum_{i=0}^{kdim}A(midx,i)*B(i,nidx) $$ 其中kdim表示A矩阵一行有kdim个分块

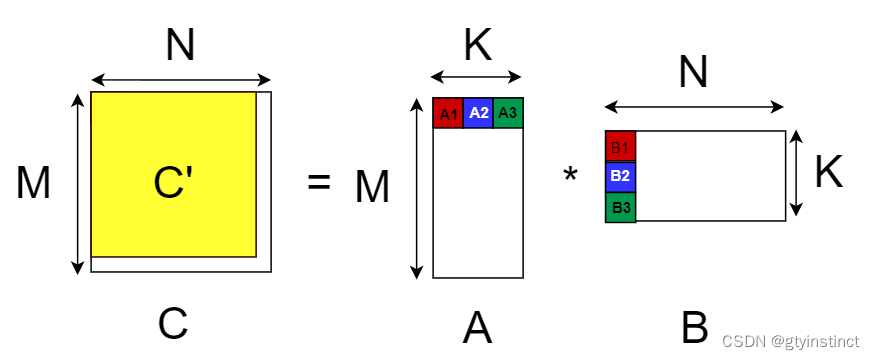
• 因此C中每一个分块可以分配给一个warp去运算，运算过程便是进行kdim次WMMA操作，而我们原来想要的C'矩阵便是填充后的C矩阵的一部分。（由于填充部分为0，所以不会对填充的部分不会对C’矩阵的值有影响）

BMMA

• 其实C中的每一个分块也可以分配给一个block去计算，即block matrix multiply-accumulate（block级别矩阵乘加速）
• 这样可以将kdim个WMMA操作分配给block内的不同warp去计算，并把结果写回到share memory中
• 之后同步操作，将share memory中存储的不同warp计算的分块结果累加到C中的分块

实现代码

• GEMM_wmma 实现了warp level 矩阵乘加速（通过WMMA调用tensor core）

• GEMM_bmma 实现了block level 矩阵乘加速 (通过WMMA调用 tensor core)

• gemm.cu 对比 GEMM_wmma 、 GEMM_bmma 和 cutlass 中的basic_gemm运算结果和速度

运行方法

make CUTLASS_DIR=your_cutlass_dir ARCH=your_arch NAME=gemm run

或直接修改Makefile后运行

make run

Log

time	content
2022-7-25	use unify memory for cuda_data