拖了半年了。。 回来更新一波
赛题详见 天池-菜鸟需求预测与分仓规划
- 最终第二赛季线上成绩第10
- 数据集
- 总共140W条需要预测的数据,其中20W是全国的,另外6个分仓各有20W
- 要预测的是 2015.12.28~2016.01.10的销量
- 数据预处理
- 我们只是简单的去掉了11.11与12.12一整天的数据,然后将之前的日期往前平移
- 训练集
- 线上选取的是2015.12.14~2016.12.27日作为训练样本,线下以其作为验证集,选取2015.11.30~2015.12.13作为线下训练集
- 特征
- 窗口特征 ( 前 1、2、3、4、7、14、21、28)
- 根据商品、叶子类目、大类目、品牌、供应商进行分组,提取前X天的非聚划算支付人次、浏览数、加购数的平均值、最小值、标准差作为特征
- 商品特征
- 商品最早出现历史数据的日期距离要预测的那一周的天数
- 商品最后一次出现历史数据的日期距离要预测的那一周的天数
- 商品的折扣率(成交价格 / 拍下价格)
- 商品的平均成交价格
- 特征缺失值全部填**-1**(填-1的效果比填0好)
- 受限于自己实现的GBRT的速度,最后通过一些简单的特征选择方法及人工选择,特征只剩下了150维左右
- 窗口特征 ( 前 1、2、3、4、7、14、21、28)
- 模型
-
评价函数
- 函数
- +B_iMAX(T_i-D_i,0)] )
- 对于每个样本来说,补高和补低的成本是不一样的
Quantile Regression- https://en.wikipedia.org/wiki/Quantile_regression
- scikit-learn中的GradientBoostingRegression中支持
loss = 'quantile', 具体的loss function可以简单看做是在 lad loss(MAE)的基础上,对于补高和补低分开计算loss,使用一个参数 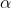 调整补高补低的比例。 - } + (1-\alpha)|y^*-p|{(y^*<p)} )
- 函数
-
针对赛题结合Quantile Regression提出的模型
- 简单变形
- +B_i / A_i*MAX(T_i-D_i,0)] )
- 于是,可以将 看作是样本权重, 剩下的部分直接就是
quantile loss - 然后我们对每个商品的 做了简单的统计,然后按这个值将所有样本划分为10个区间,每个区间14W个样本(其实就是近似认为同一个区间内的所有样本在quantile loss 中的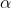 参数一样)
- 最终单模型
- 对10个模型分别训练预测,简单的调节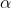 参数,即可得到一个很不错的结果。
- 后续融合
- 我们最终只使用了GBRT一个模型,调整了其深度,学习率,行采样、列采样率进行平均融合。
- 分仓数据(0.3)和全国数据(0.7)加权融合
- 简单变形
-
关于模型
- 在这次比赛中我参考了scikit-learn的源码实现了比较简单的Java的Decision Tree 及 GradientBoostingTree
- 很明显MapReduce下难以实现并行的GBRT,因此我们最后的结果就是10个模型并行在10个reducer上
-
后续提升idea
- 对label进行log变换
- 对新商品使用规则
- 使用我在广东机场大赛中实现的随机森林
- 增加特征、增加训练集。。。。
-