https://github.com/kiyoxi2020/Singular-Spectrum-Analysis.git
Sacchi, M. D. (2009). FX singular spectrum analysis. CSPG CSEG CWLS Convention.
-
Singular Spectrum Analysis (SSA)奇异谱分析,一种基于Hankel矩阵的特征谱分解方法
-
考虑一个二维信号,该信号由一个相同的一维波形经过时间方向的固定偏移形成,即有一个固定的倾角,该信号的时域(TX)、频域(FX)表示写作:
$$ s(t,x)=w(t-px)\Leftrightarrow S(\omega,x)=W(\omega)e^{-i\omega px} $$ 考虑一个固定频率($\omega$ )、均匀采样($x=(k-1)\Delta x$)的数据,该数据的FX域表示为(为便于表示,省略$\omega$): $$ S_n=We^{-i\alpha n} $$ 其中,$\alpha=\omega p\Delta x$,对于任意两个相邻道,可以得到递推关系: $$ S_n=PS_{n-1} $$
-
上式假设信号在空间是可预测的,可以构建Hankel矩阵: $$ M=\left(\begin{matrix}S_1&S_2&S_3&S_4\ S_2&S_3&S_4&S_5\S_3&S_4&S_5&S_6\S_4&S_5&S_6&S_7\end{matrix}\right) $$ 将递推式代入,可得: $$ M=\left(\begin{matrix}S_1&PS_1&P^2S_1&P^3S_1\ PS_1&P^2S_1&P^3S_1&P^4S_1\P^2S_1&P^3S_1&P^4S_1&P^5S_1\P^3S_1&P^4S_1&P^5S_1&P^6S_1\end{matrix}\right) $$
易见,以上矩阵的秩为$r=1$,通过上述操作,我们得到了一个降秩后的矩阵。同理可得,若有$L$种偏移方式,则矩阵的秩应为$r=L$,因此可以通过SVD分解对上式进行降秩: $$ \hat{M}=\sum_{k=1}^L \lambda_k u_k v_k^H $$
即取前$L$个特征值实现矩阵降秩,再基于降秩矩阵进行重构即可实现对原始信号的重构。
-
最后沿逆对角线方向进行均值滤波: $$ \hat{s}=A(\hat{M}) $$
其中,算子$A$表示沿着逆对角线方向对降秩后的Hankel矩阵$\hat{M}$进行均值滤波
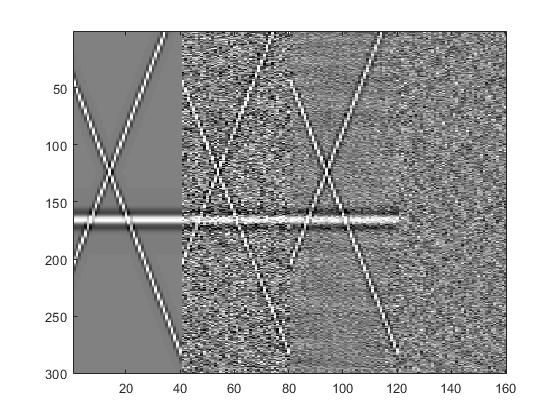
- 运行main_denoise_2d.m即可实现基于SSA的去噪,结果如下所示:
从左至右分别为:干净信号、有噪信号、去噪结果、去除噪声