Physics-informed convolutional-recurrent neural networks for solving spatiotemporal PDEs
Paper link: [Journal Paper], [ArXiv]
By: Pu Ren, Chengping Rao, Yang Liu, Jian-Xun Wang and Hao Sun
- Present a Physics-informed discrete learning framework for solving spatiotemporal PDEs without any labeled data
- Proposed an encoder-decoder convolutional-recurrent scheme for low-dimensional feature extraction
- Employ hard-encoding of initial and boundary conditions
- Incorporate autoregressive and residual connections to explicitly simulate the time marching
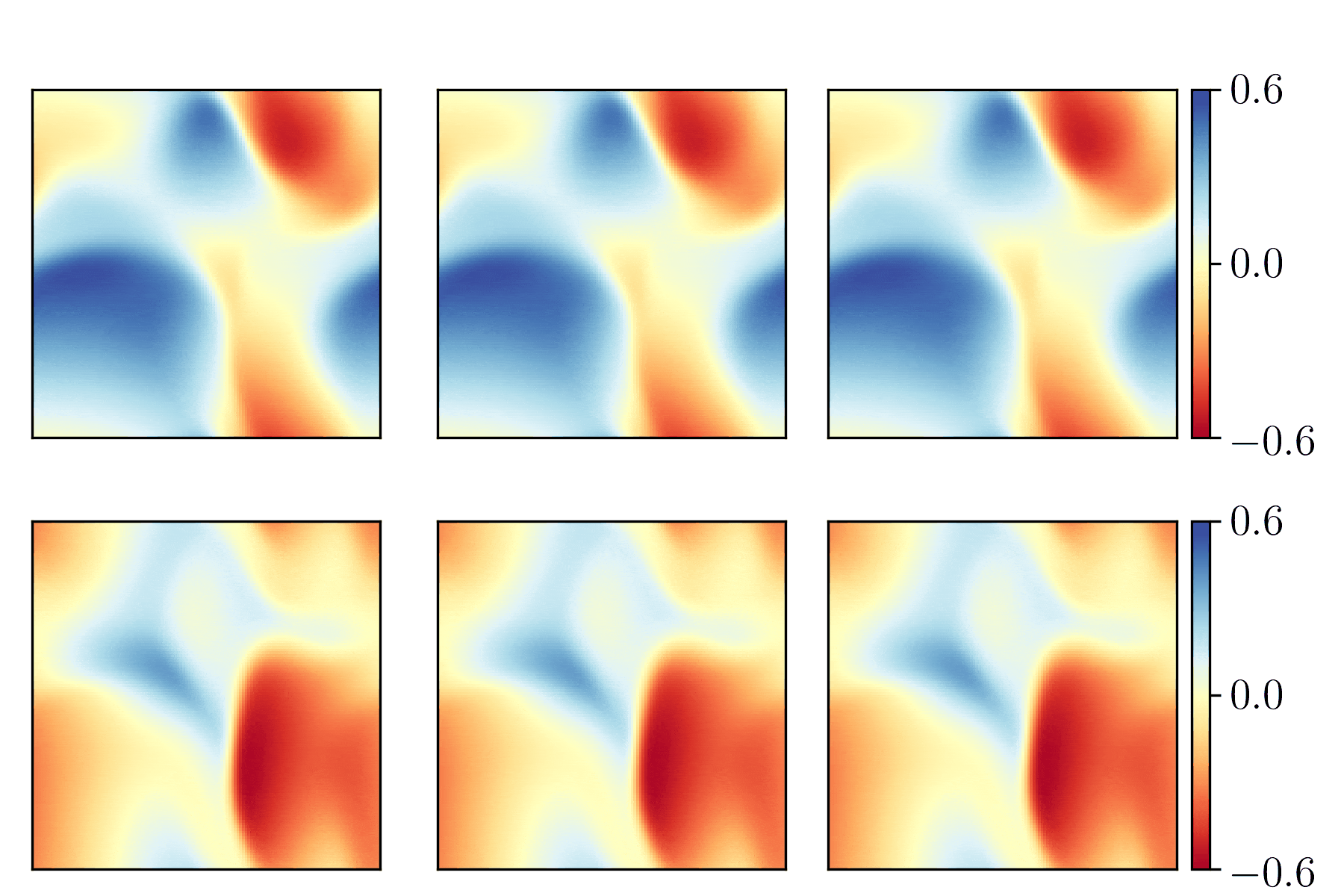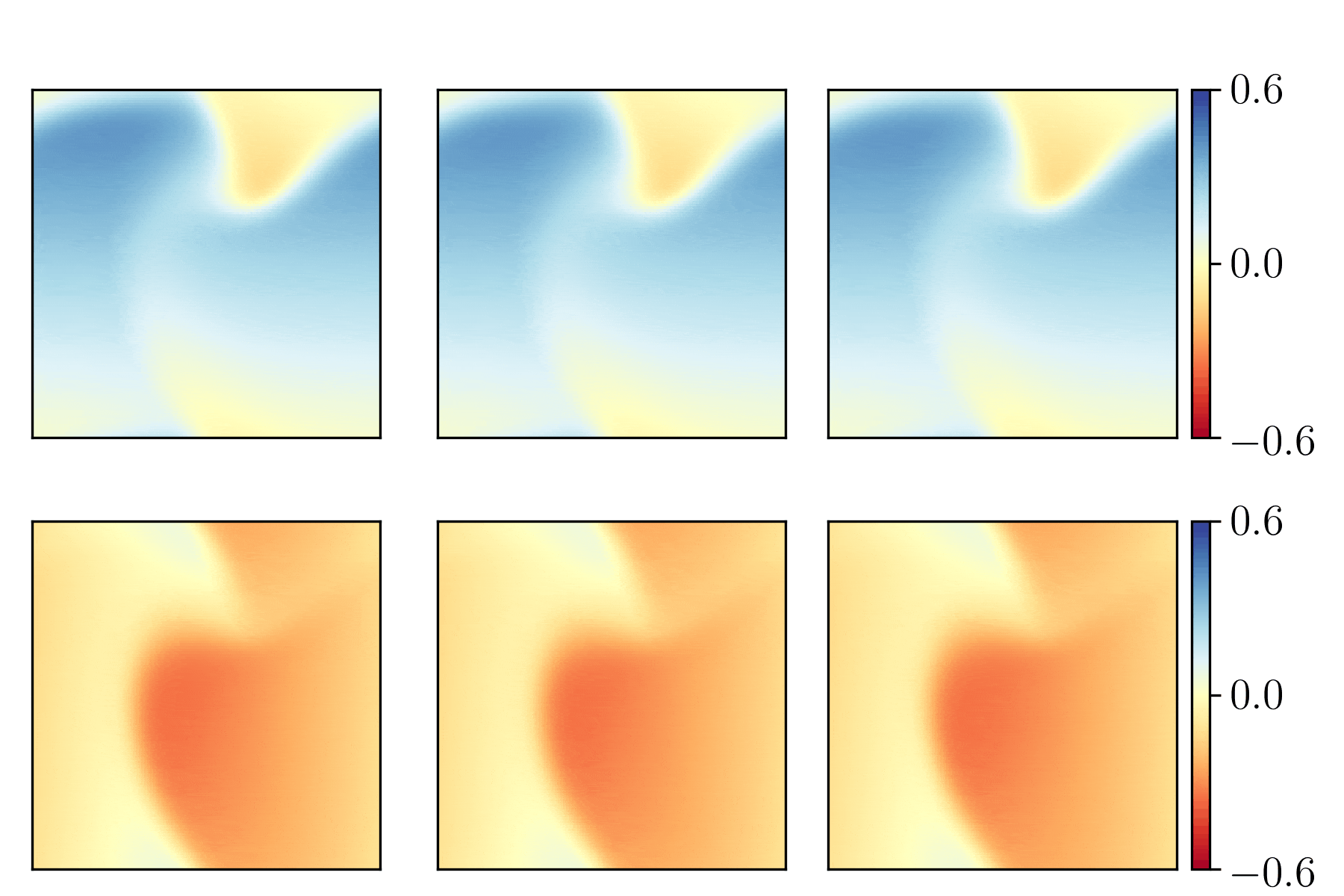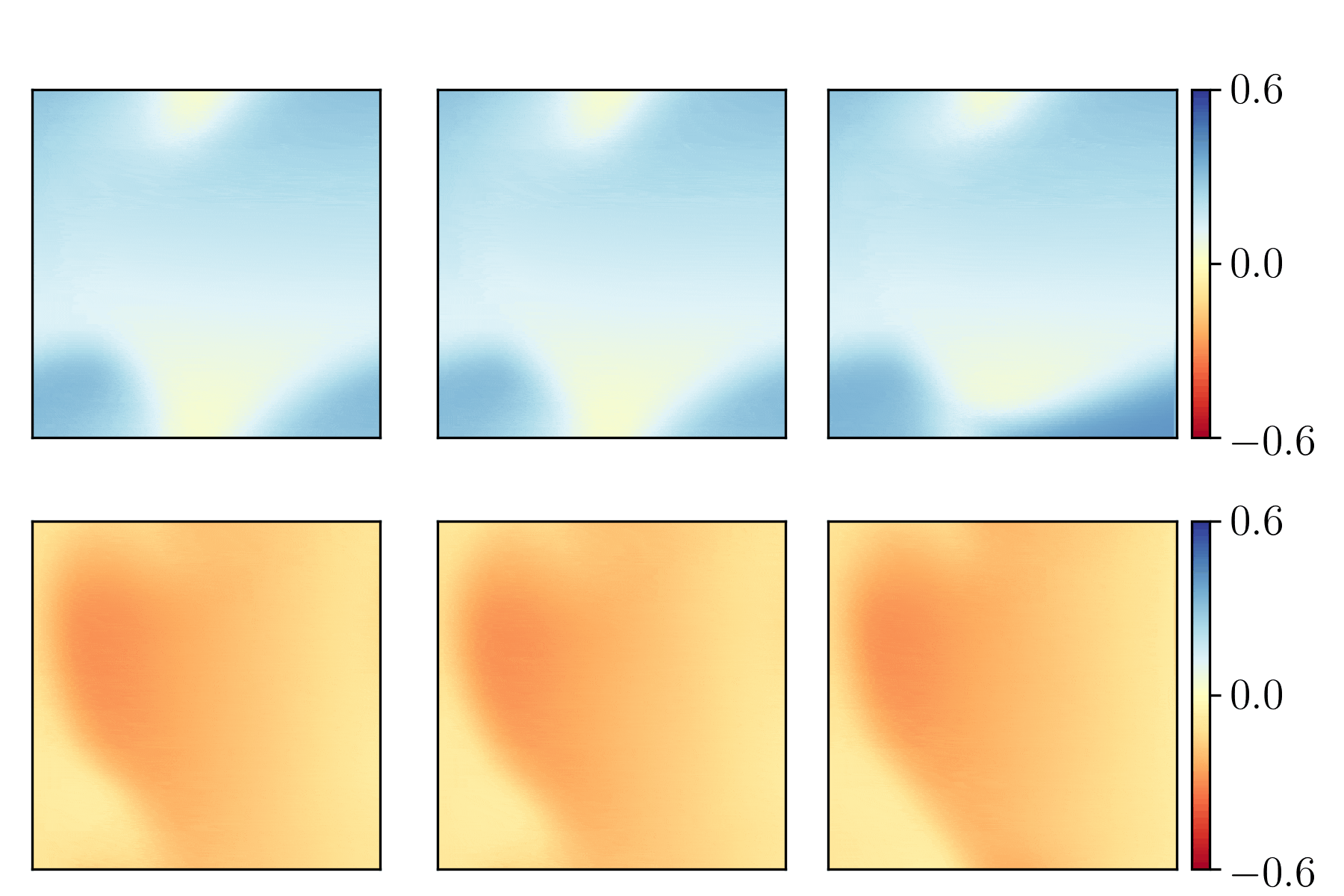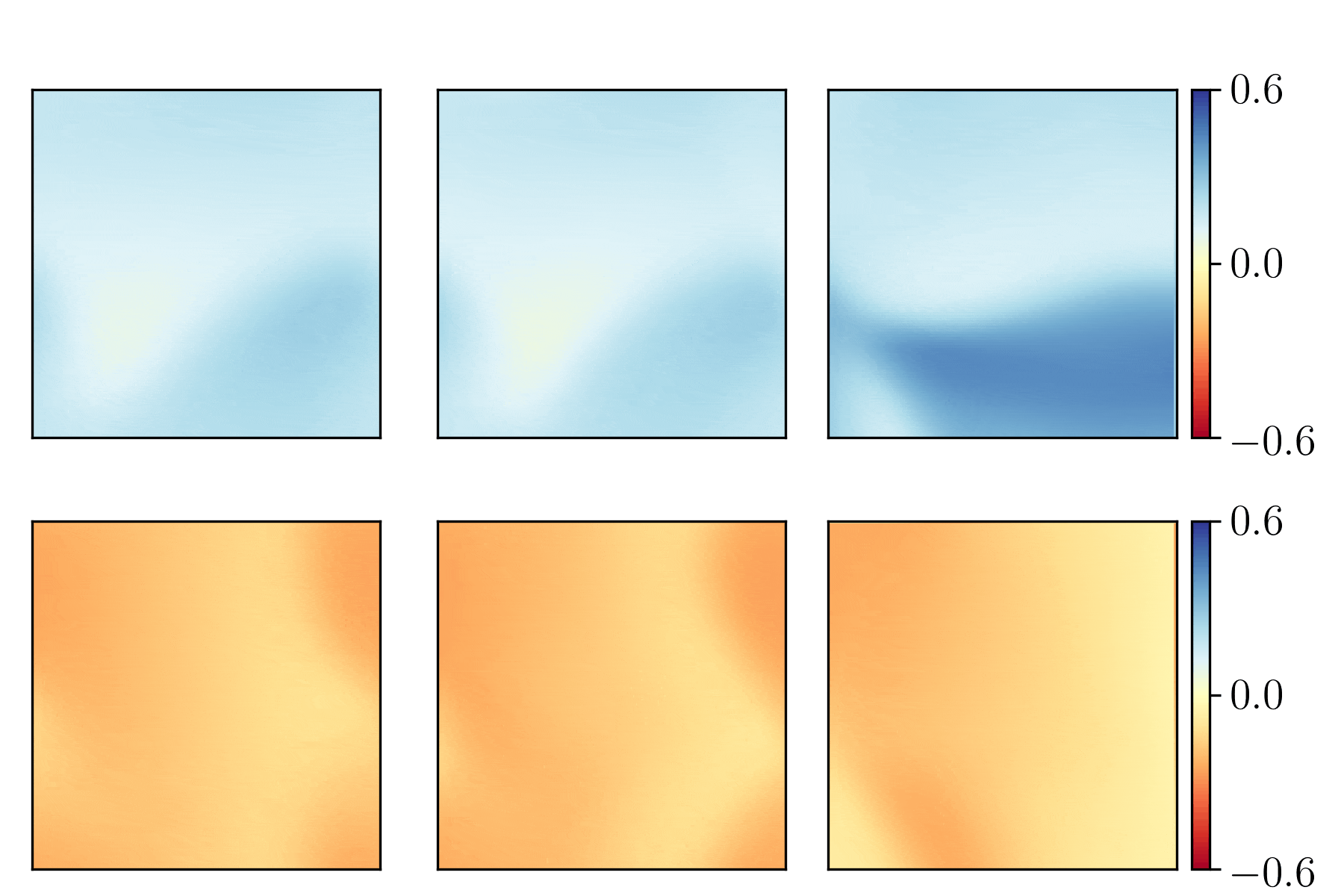
Here we show the comparison between PhyCRNet and PINN on 2D Burgers' equations below. The left, middle and right figures are the ground truth, the result from our PhyCRNet and the result from PINNs respectively.
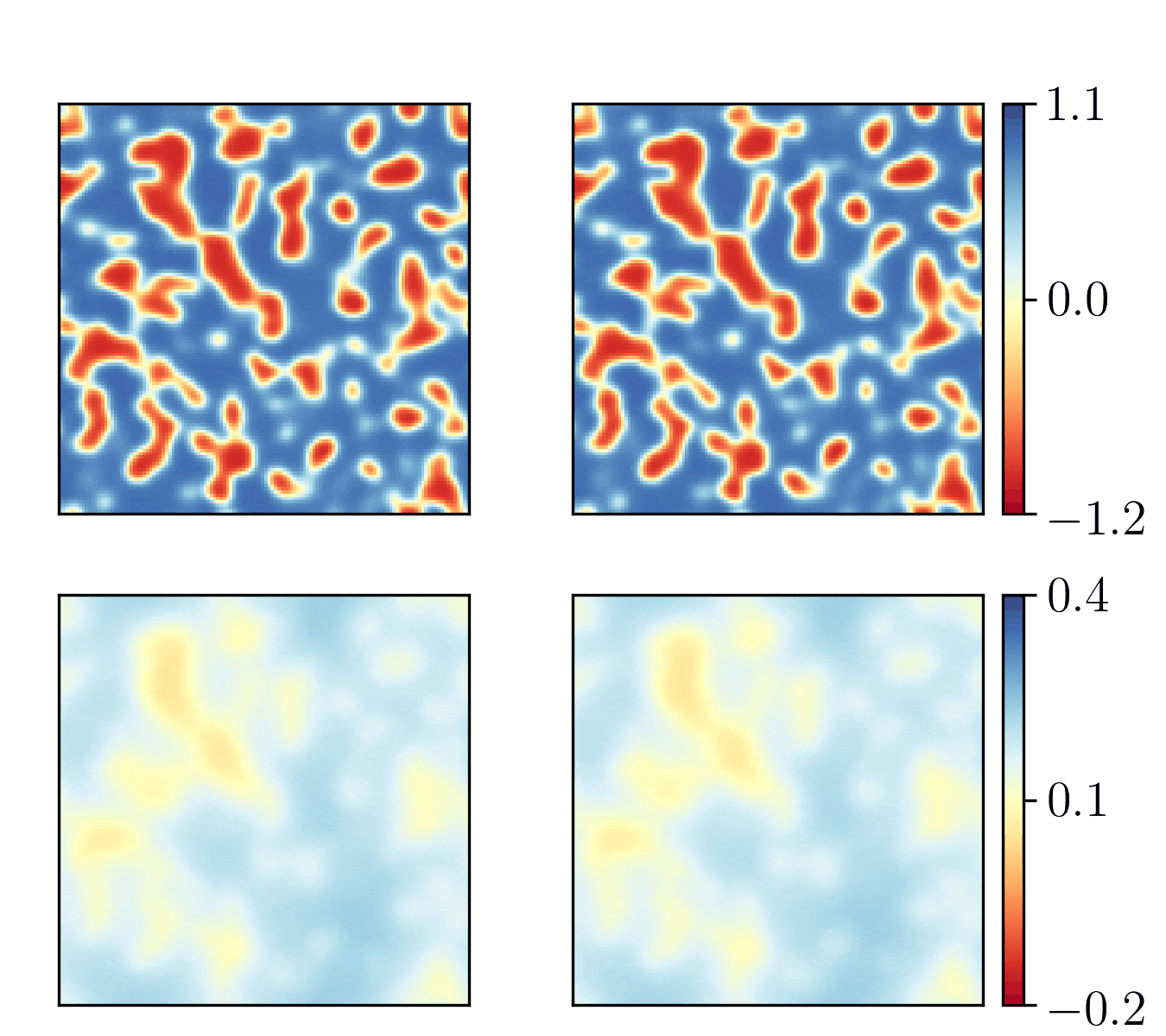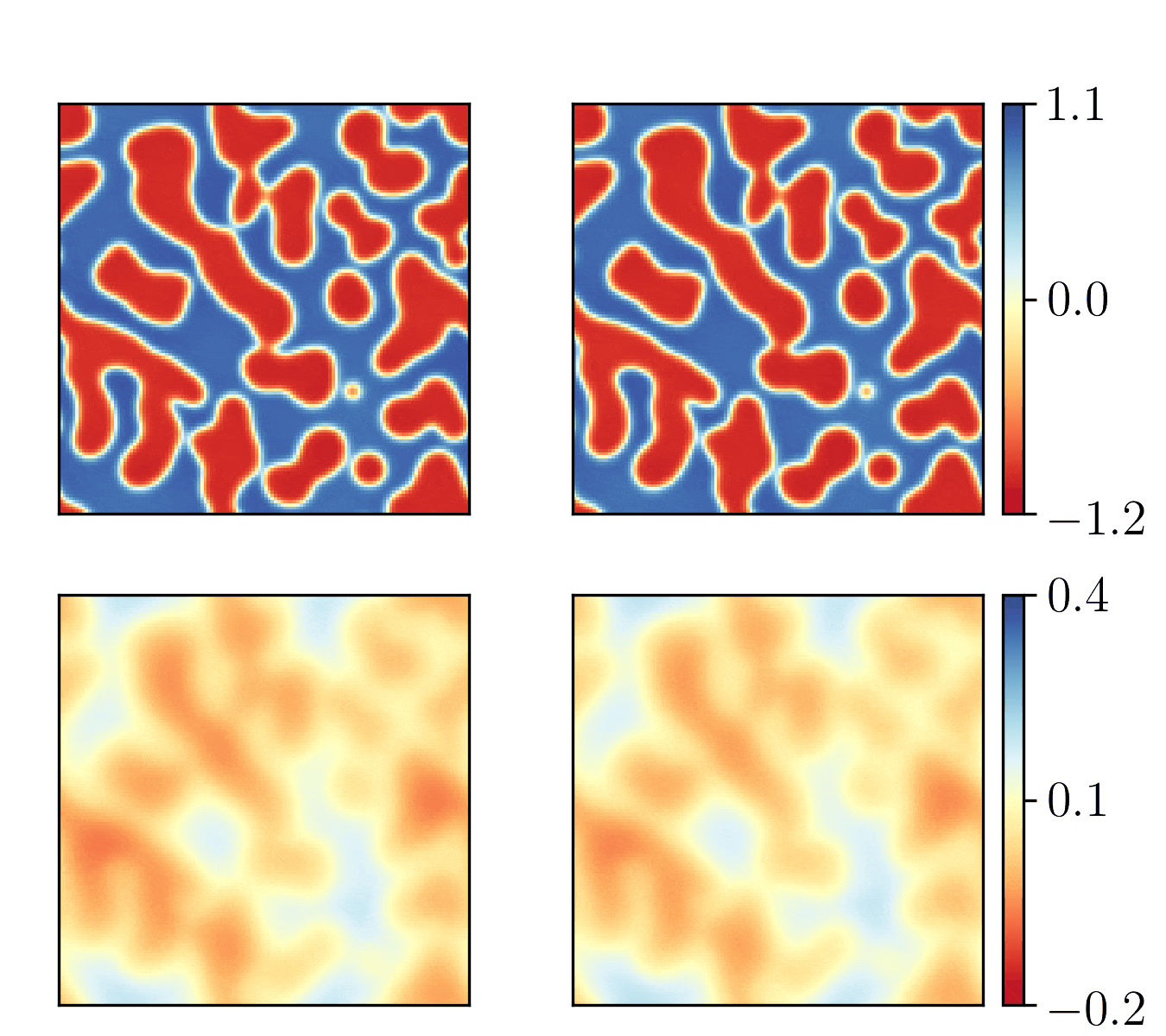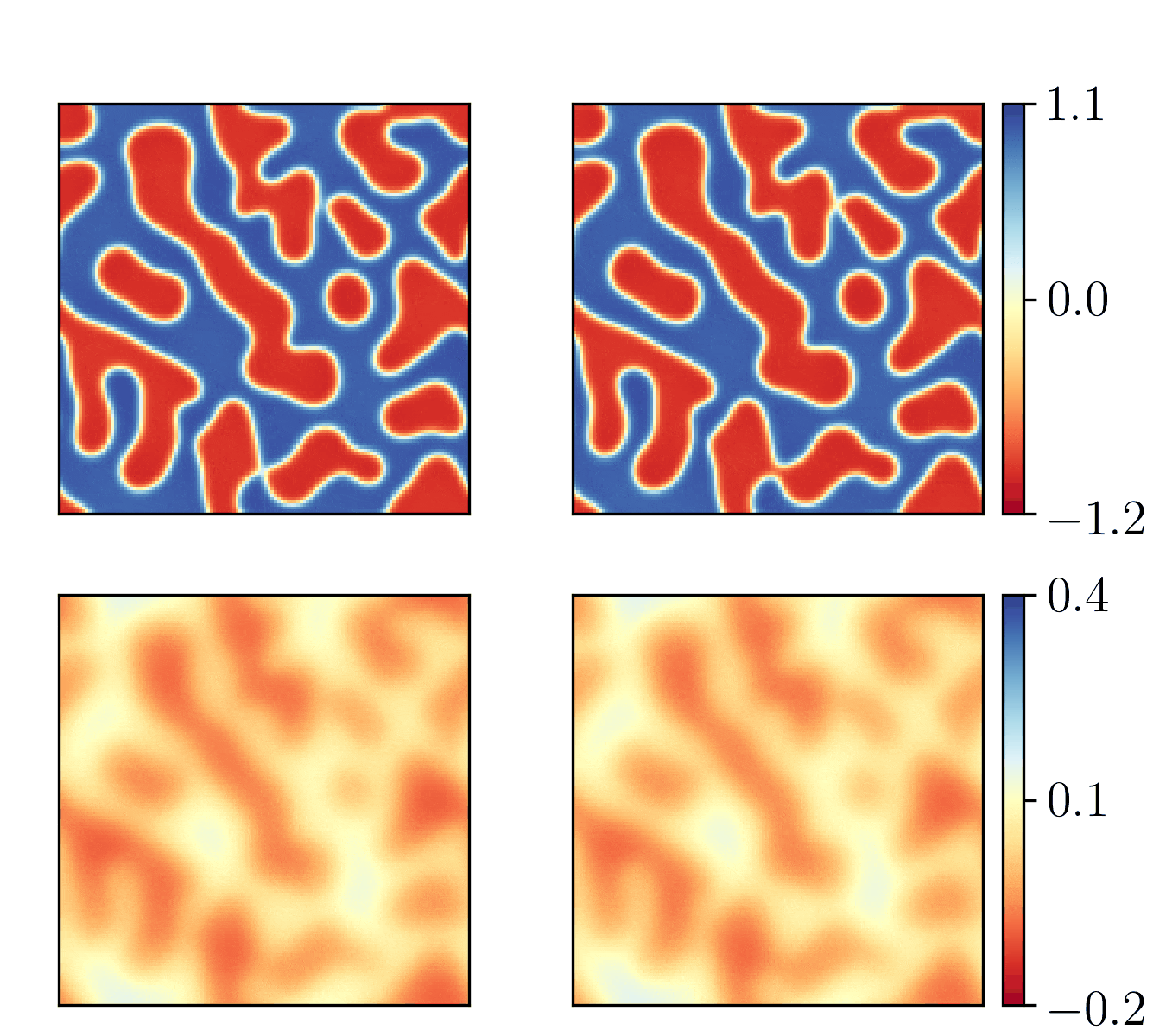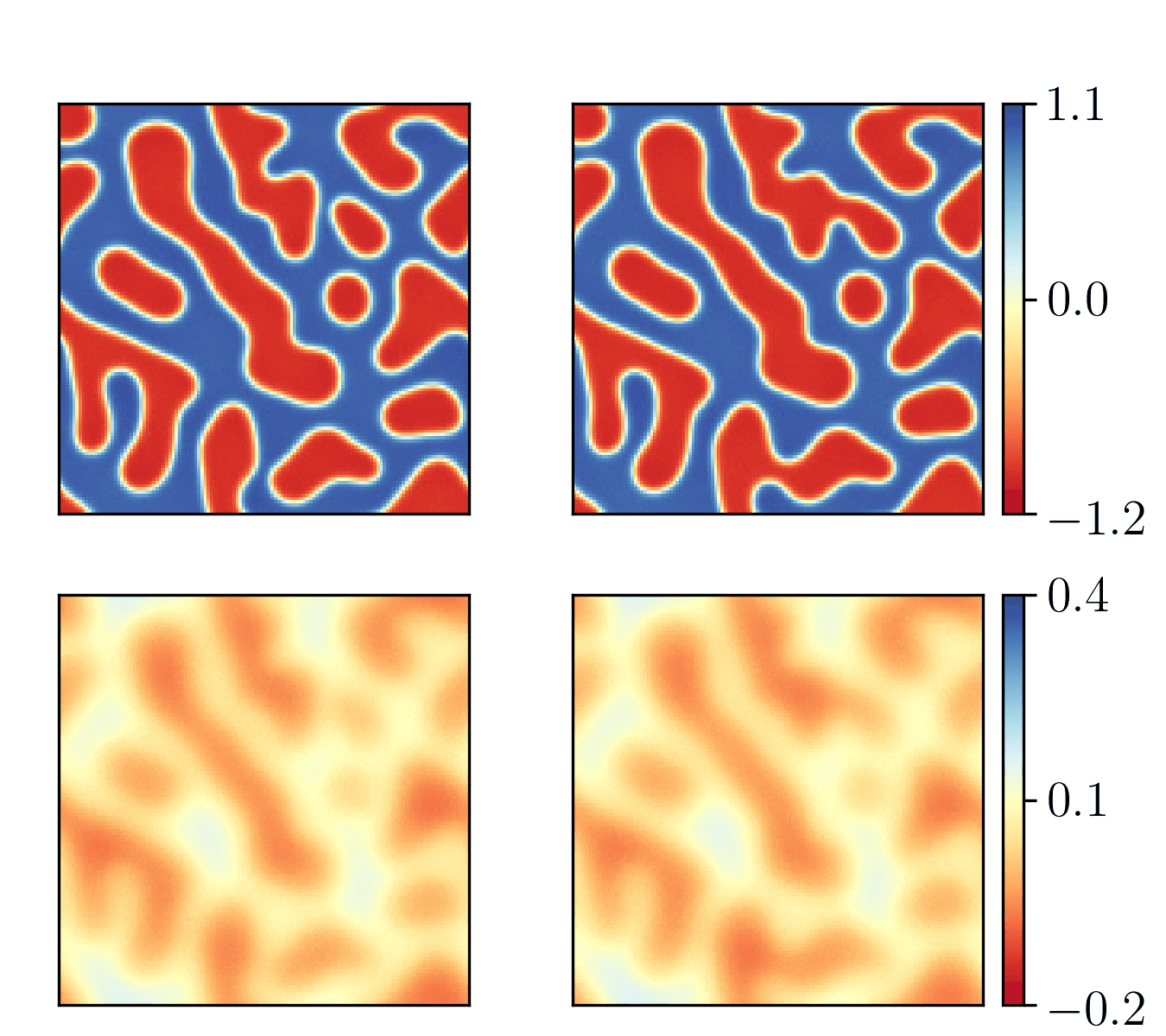
We show the generalization test on FitzHugh-Nagumo reaction-diffusion equations with four different initial conditions. The left and right parts are the ground truth generated with the high-order finite difference method and the results from our PhyCRNet, respectively.
- Python 3.6.13
- Pytorch 1.6.0
- Other packages, such as Matplotlib, Numpy and Scipy, are also used
We provide the codes for data generation used in this paper, including 2D Burgers' equations and 2D FitzHugh-Nagumo reaction-diffusion equations. They are coded in the high-order finite difference method. Besides, the code for random field is modified from [Link]. You may find the data solver for λ-ω reaction-diffusion equations in [Link].
The initial conditions tested in this paper are also provided in the folder Datasets.
The general code of PhyCRNet is provided in the folder Codes, where we use 2D Burgers' equations as a testing example. For other PDE systems, the network setting is similar. You may try modifying the grid sizes and time steps to your own cases.
It is important to pretrain the network from a small number of time steps (e.g., 100) and then gradually train on a longer dynamical evolution. Taking 2D Burgers' equation as an example, we pretrain the model from 100, then 200 and 500, and finally 1000. The model is able to extrapolate for at least another 1000 time steps.
If you find our research helpful, please consider citing us with:
@article{ren2022phycrnet,
title={PhyCRNet: Physics-informed convolutional-recurrent network for solving spatiotemporal PDEs},
author={Ren, Pu and Rao, Chengping and Liu, Yang and Wang, Jian-Xun and Sun, Hao},
journal={Computer Methods in Applied Mechanics and Engineering},
volume={389},
pages={114399},
year={2022},
publisher={Elsevier}
}