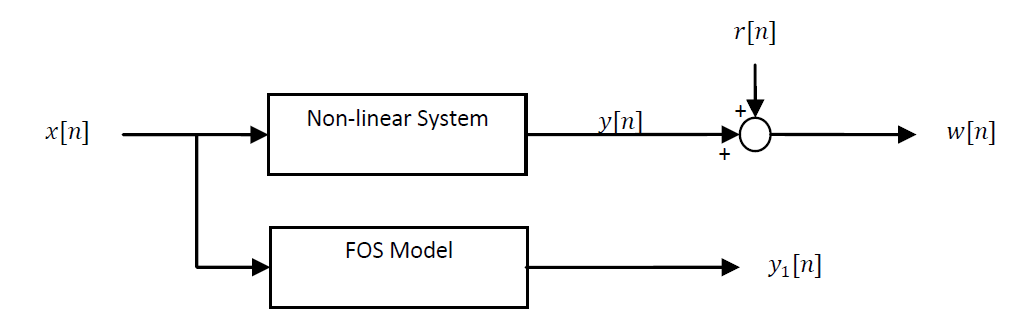
Implementation of Fast Orthogonal Search (FOS) Algorithm as described in this paper:
@article{Korenberg:1989:ROA:2733743.2733908,
author = {Korenberg, M. J.},
title = {A Robust Orthogonal Algorithm for System Identification and Time-series Analysis},
journal = {Biol. Cybern.},
issue_date = {February 1989},
volume = {60},
number = {4},
month = feb,
year = {1989},
issn = {0340-1200},
pages = {267--276},
numpages = {10},
url = {http://dx.doi.org/10.1007/BF00204124},
doi = {10.1007/BF00204124},
acmid = {2733908},
publisher = {Springer-Verlag New York, Inc.},
address = {Secaucus, NJ, USA},
}
FOS tries to provide a mathematical model to map the input signal of a system to its output signal, using a time-series polynomail equation.
For a system that produces, at epoch , output
for input
, FOS tries to model the output as a summation of polynomial terms:
where each polyomial term,
is a product of inputs and/or outputs, possibly at different epochs:
such that:
The FOS algorithm aims to minimize the error between the actual output,
and the predicted output,
.
,
and
are paremeters to the FOS algorithm and are therefore determined by the user:
is the maximum order of the polynomial
is the maximum lag in input that the current output can depend on
is the maximum lag in output that the current output can depend on
If, and
are set to zero, then FOS will aim to find the relationship between the input and output for a time-independent system.
We advise you to run tests test1.m and test2.m and go through their code to understand how to train and evaluate a model using FOS.
If you find this code useful in your work, please cite the following paper by the author of the code:
@article{ElhoushiSurvvey2017,
author = {Elhoushi, Mostafa and Georgy, Jacques and Noureldin, Aboelmagd and Korenberg, Michael J.},
title = {A Survey on Approaches of Motion Mode Recognition Using Sensors},
journal = {IEEE Trans. Intelligent Transportation Systems},
keywords = {activity_recognition},
number = 7,
pages = {1662-1686},
url = {https://ieeexplore.ieee.org/document/7726001},
volume = 18,
year = 2017
}