Rethinking the Design of Learning based Inter-Patient Registration using Deformable Supervoxels (MIDL 2021) https://openreview.net/forum?id=zZA5TpNdC4Z
This repository provides open source code for our SLIC_Reg approach for 3D deformable image registration.
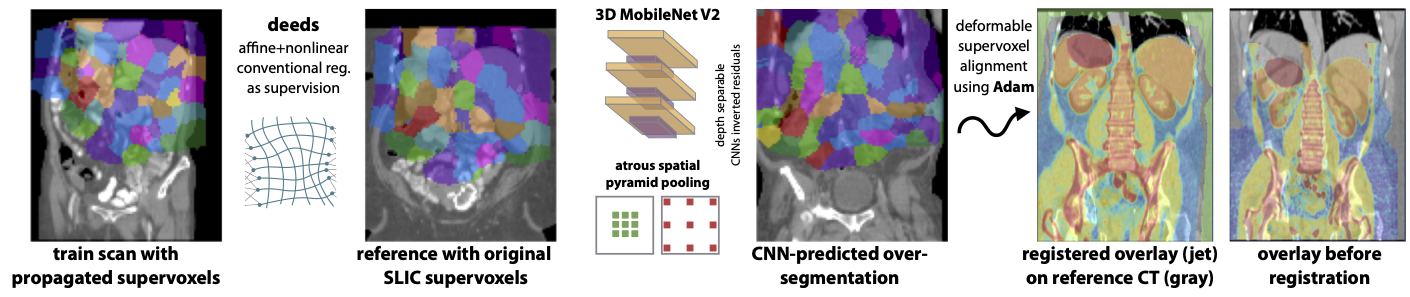
Our method radically changes the design of learning based registration by replacing the often unstable regression target with automatic supervoxel predictions. That means we solve registration by segmentation, yet not in a semantic way where anatomical labels are required but purely based on local geometry. Slic-Reg uses a 3D DeepLabout architecture with multiple heads and outperforms PDD-Net (state-of-the-art for unsupervised DL registration in the Learn2Reg challenge) and regression (as well as UNet architectures):
| Method | Initial | PDD | Regression | Slic-UNet | Slic-Reg |
|---|---|---|---|---|---|
| Spleen (1) | 18.0% | 48.8% | 31.1% | 57.1% | 62.4% |
| Right Kidney (2) | 12.5% | 49.0% | 45.6% | 38.4% | 50.8% |
| Left Kidney (3) | 9.0% | 42.3% | 43.2% | 41.8% | 49.1% |
| Liver (6) | 26.2% | 71.1% | 57.7% | 71.8% | 74.1% |
| Avg. 4 (1,2,3,6) | 16.4% | 50.1% | 44.4% | 52.3% | 59.1% |
| Avg. 13 | 8.8% | 29.1% | 25.1% | 30.0% | 31.8% |
The dataset used in this paper is a pre-processed version of the "Beyond the Cranial Vault" MICCAI challenge on abomdinal CT and contains manual segmentations of the following 13 anatomies right kidney, left kidney, gallbladder, esophagus, liver, stomach, aorta, inferior vena cava, portal vein, pancreas, right adrenal gland, left adrenal gland. It contains 30 public scans that were split into training (#2,3,5,6,8,9,21,22,24,25,27,28,30,31,33,34,36,37,39,40) and validation (#1,4,7,10,23,26,29,32,35,38) out of which #38 was selected as template. The data can be obtained here: https://cloud.imi.uni-luebeck.de/s/c9GapHY3cx9x82p (648 MBytes) Please cite: http://discovery.ucl.ac.uk/1501854/1/Modat_TBME-01460-2015.R2-preprint.pdf if you use this data and register at https://www.synapse.org/#!Synapse:syn3193805/wiki/89480 for the original access.
The original scans were resampled to isotropic 2mm resolution using c3d (c3d img/img0002.nii.gz -resample-mm 2x2x2mm) and cropped to our target shape 192x160x256 as follows. A centre of mass was computed from the following weight tensor (using Houndsfield units):
weight = torch.sigmoid(10-10*torch.abs((data-0)/250*2-1)).unsqueeze(0).unsqueeze(0)
weight2 = -F.max_pool3d(-weight,3,stride=1,padding=1).squeeze(0)
centre = torch.sum(xyz*weight2,[1,2,3])/(0.0001+torch.sum(weight2,[1,2,3]))
From this an affine_grid to transform the scan and segmentation can be directly obtained.
Our SLIC_REG method comprises the following steps:
A single template scan is selected (as fixed scane) from which both linear and deformable transformations are estimated to all training images without any supervision. For this step we employ both linear and nonlinear registration of the deeds algorithm: https://github.com/mattiaspaul/deedsBCV with default parameters, e.g.
./linearBCV -F Training/img/img0002.nii.gz -M Training/img/img0038.nii.gz -O baseline/F02_38
./deedsBCV -F Training/img/img0002.nii.gz -M Training/img/img0038.nii.gz -A baseline/F02_38_matrix.txt -O baseline/F02_38
This results in 20 affine matrices and 20 nonlinear displacement fields (e.g. baseline/F02_38_displacements.dat). To read in those displacements and convert the values to a pytorch grid_sample compatible format use:
with open('baseline/F02_38_displacements.dat', 'rb') as content_file:
content = content_file.read()
grid_space = int((torch.pow(torch.Tensor([H*W*D])/(len(content)/12),0.334)))
with torch.no_grad():
disp_field = torch.from_numpy(np.array(struct.unpack('f'*(len(content)//4),content))).reshape(1,3,D//grid_space,W//grid_space,H//grid_space).cuda().permute(0,1,4,3,2).float()
disp_field = F.interpolate(disp_field,size=(H,W,D),mode='trilinear',align_corners=None).permute(0,2,3,4,1)[:,:,:,:,torch.Tensor([2,0,1]).long()].flip(4)
disp_torch = disp_field.flip(4)/torch.Tensor([256-1,160-1,192-1]).cuda().view(1,1,1,1,3)*2
The template scan is automatically over segmented using the SLIC supervoxel algorithm with subsequent post-processing to obtain an equal number (here 127 + background) of connected supervoxels within a rough body mask. A single 3D oversegmentation is obtained using the skimage toolkit for SLIC:
cluster = skimage.segmentation.slic(img_aff[i,0].cpu().numpy(),multichannel=False,mask=sdt_aff[i,0].cpu().numpy()<30,\
compactness=1.5, enforce_connectivity=True, max_iter=5, n_segments=208, min_size_factor=0.85)
Here, img_aff is the reference scan transformed with a random affine matrix and sdt_aff the signed distance transform of its corresponding foreground mask (by choosing <30 this is dilated by 30 voxels or 60 mm ensuring that nearly the whole body is registered).
This step is repeated 16 times with slightly varying initialisations so that each voxel can be identified by a 16-tuple of supervoxels (please also see (Heinrich et al., 2013) for details http://www.mpheinrich.de/pub/IPMI2013_mycopy.pdf). By simultaneously assigning each voxel to multiple layers of supervoxels its spatial position in the canonical space of reference coordinates is more accurately defined as outlined in the following sketch:

Unfortunately, the number of superpixels returned by skimage.segmentation is not always equal to n_segments. Hence, we implemented a post-processing that iteratively merges smaller segments until 127 foreground and one background supervoxels are reached (see code for details). Next, the reference supervoxels are spatially transferred to all training images using deeds’ displacement fields. Since, all these sub-steps are a bit cumbersome we are also providing all warped pre-processed supervoxels as download: https://cloud.imi.uni-luebeck.de/s/GaMekWkAnrErDgj (Note that each voxel in each training/reference image is now assigned to 16 classes (0..127)).
Next, a deep CNN is trained to densely predict the over-segmentations for unseen images (see Fig. 1 for a qualitative result). We designed a compact 3D DeepLab (MobileNetV2 with ASPP) (Sandler et al., 2018) for best performance on a small dataset. The ASPP module is simply changed to 3D from https://github.com/pytorch/vision/blob/master/torchvision/models/segmentation/deeplabv3.py but the MobileNetV2 backbone is specifically adapted to our needs as follows:
class ResBlock(torch.nn.Module):
def __init__(self, module):
super().__init__()
self.module = module
def forward(self, inputs):
return self.module(inputs) + inputs
in_channels = torch.Tensor([1,24,24,32,48,48,48,64]).long()
mid_channels = torch.Tensor([64,128,192,192,256,256,256,384]).long()
out_channels = torch.Tensor([24,24,32,48,48,48,64,64]).long()
mid_stride = torch.Tensor([1,1,1,2,1,1,1,1])
net = []
net.append(nn.Identity())
for i in range(8):
inc = int(in_channels[i]); midc = int(mid_channels[i]); outc = int(out_channels[i]); strd = int(mid_stride[i])
layer = nn.Sequential(nn.Conv3d(inc,midc,1,bias=False),nn.BatchNorm3d(midc),nn.ReLU6(True),\
nn.Conv3d(midc,midc,3,stride=strd,padding=1,bias=False,groups=midc),nn.BatchNorm3d(midc),nn.ReLU6(True),\
nn.Conv3d(midc,outc,1,bias=False),nn.BatchNorm3d(outc))
if(i==0):
layer[0] = nn.Conv3d(inc,midc,3,padding=1,stride=2,bias=False)
if((inc==outc)&(strd==1)):
net.append(ResBlock(layer))
else:
net.append(layer)
backbone = nn.Sequential(*net)
This results in only about 220k trainable parameters and we use residual were possible (same stride and in/out channels). We use kaiming_normal weight initialisation and later add a single skip connection to improve segmentation detail. After applying the atrous spatial pyramid pooling, which is essential to capture context, we use a head with groups=16 and channels x 16, so that for each voxel a total of 16 softmax scores (with 128 class probabilities) are estimated:
aspp = ASPP(64,(2,4,8,16),128)#ASPP(64,(1,),128)
num_classes = 128 #input 128 + 24 (from skip)
head = nn.Sequential(nn.Conv3d((128+24), 32*16, 1, padding=0,groups=1, bias=False),nn.BatchNorm3d(32*16),nn.ReLU(),\
nn.Conv3d(32*16, 32*16, 3, groups=16,padding=1, bias=False),nn.BatchNorm3d(32*16),nn.ReLU(),\
nn.Conv3d(32*16, num_classes*16, 1,groups=16))
A complete forward path (using memory checkpointing) is defined as follows:
x1 = checkpoint(backbone[:3],input)
x2 = checkpoint(backbone[3:],x1)
y = checkpoint(aspp,x2)
#skip-connection at backbone[3]
for j in range(4): #unroll mini-batch for head
y1 = torch.cat((x1[j:j+1],F.interpolate(y[j:j+1],scale_factor=2)),1)
output_j = checkpoint(head,y1)
We trained the prediction of supervoxels for 3000 iterations with a mini-batch size of 4 (600 epochs) using Adam with lr=0.004 in less than 1 hour. We used an RTX2070 card with TensorCores enabled (through compiling pytorch 1.9 from source with CuDNN 8.1) and automatic mixed precision. Affine augmentations are used to transform training images and supervoxel segmentations on the fly:
affine = F.affine_grid(torch.eye(3,4).unsqueeze(0)+torch.randn(4,3,4)*.07,(4,1,96,80,128)).cuda()
We trained the prediction of supervoxels for 3000 iterations with a mini-batch size of 4 (600 epochs) using Adam with lr=0.004 in less than 1 hour. We used an RTX2070 card with TensorCores enabled (through compiling pytorch 1.9 from source with CuDNN 8.1) and automatic mixed precision.
Subsequently a one-to-one correspondences between reference and test image could be directly obtained. Yet, to obtain an optimal displacement field that balances the potentially diverging correspondences and avoids erroneous hard assignments, we implement another step that optimises the alignment of all supervoxels using the Adam optimiser with a diffusion regularisation penalty. The method is straightforward to implement and very fast (<1 sec for 3D registration):
lr = 0.05; alpha = 0.015; k = 8; num_iter = 100; N = 2048
def adam_optim(kpts_fixed, feat_kpts_fixed, feat_moving,alpha):
class Flow(nn.Module):
def __init__(self):
super(Flow, self).__init__()
self.flow = nn.Parameter(torch.zeros(kpts_fixed.shape))
def forward(self):
return self.flow
net = Flow().to(device)
optimizer = optim.Adam(net.parameters(), lr=lr)
weight = knn_graph(kpts_fixed, k)[2]
for iter in range(num_iter):
optimizer.zero_grad()
flow = net()
kpts_moving = kpts_fixed + flow
feat_kpts_moving = F.grid_sample(feat_moving, kpts_moving.view(1, 1, 1, -1, 3), mode='bilinear').view(1, -1, N).permute(0, 2, 1)
data_loss = F.mse_loss(feat_kpts_moving, feat_kpts_fixed)
reg_loss = (pdist(flow)*weight).sum()/(kpts_fixed.shape[1])
loss = data_loss + alpha*reg_loss
loss.backward()
optimizer.step()
return flow.detach()
kpts_fixed represents the supervoxel centres (16x128 = 2048). As input the algorithm requires floating numbers, we hence convert the argmax integers (after softmax prediction) back to a one_hot representation. To save memory and computation time, we use a smaller number of permutations (16 instead of 128) so that with 16 supervoxel layers, we have 256 channels.
You can watch a fly-through of a typical registration result, showing a warped manual segmentation using the displacements of Slic_Reg onto the target scan: https://user-images.githubusercontent.com/11568065/114840637-4cfb5000-9dd7-11eb-9a51-47a822089e2b.mov