FalconDB is an in-memory key-value storage software in C++ built as a part of CS8.401 Software Programming for Performance (Spring 2020) course project. It is capable of handling a multi-threaded benchmark application which can utilize any of the functionality 10 million times in a two minute timeframe!
-
src
- benchmark.cpp
- kvStore.cpp
-
kvStore.cpp contains the code and implementation of the data structures and all the functionality of each of the following 5 API calls that this key-value pair database supports:
- get(key,value) : Gets the value corresponding to the particular key
- put(key,value) : Insert/ overwrites the key-value pair
- del(key) : Removes the key-value pair corresponding to that key from the databse
- get(N, key, value) : Gets the Nth key-value pair (all data is lexicographically stored with respect to the keys)
- del(N) : Removes the Nthe key-value pair from the database
-
benchmark.cpp is a standard benchmark written to test the functionality of the kvStore.
- It first makes 100000 put() calls to the database
- Next a total of 1000000 random APIs are called and tested simultaneously.
- Once this is done, multithreading with the API calls is also tested.
A key-value store is a simple database that uses an associative array as the fundamental data model where each key is associated with one and only one value in a collection.
Key-value stores have no query language. They provide a way to store, retrieve and update data using simple get, put and delete commands; the path to retrieve data is a direct request to the object in memory. The simplicity of this model makes a key-value store fast, easy to use, scalable, portable and flexible.
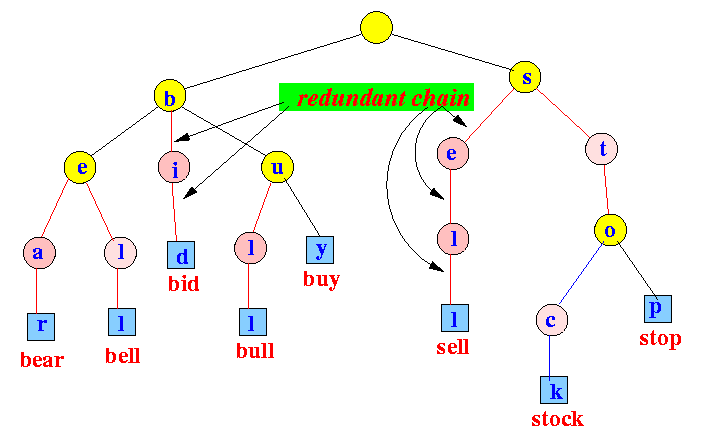
A trie is a multiway tree structure that stores sets of strings by successively partitioning them. Tries have two properties that cannot be easily imposed on data structures based on binary search.
First, strings are clustered by shared prefix. Second, there is a great reduction in the number of string comparisons—an important characteristic, as a major obstacle to efficiency is excessive numbers of string comparisons. Tries can be rapidly traversed and offer good worst-case performance, without the overhead of balancing.
Radix Trie is a specialized set data structure based on the trie that is used to store a set of strings. In contrast with a regular trie, the edges of a radix trie are labelled with sequences of characters rather than with single characters. These can be strings of characters, bit strings such as integers or IP addresses, or generally arbitrary sequences of objects in lexicographical order.
| Regular Trie | Compressed Trie |
|---|---|
 |
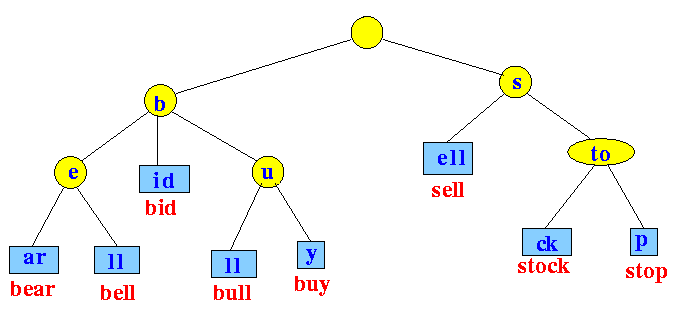 |
The radix tree is easiest to understand as a space-optimized trie where each node with only one child is merged with its child. The result is that every internal node has at least two children. Unlike in regular tries, edges can be labeled with sequences of characters as well as single characters. This makes them much more efficient for small sets and for sets of strings that share long prefixes.
Compressed Trie supports the following main operations, all of which are O(k), where k is the maximum length of all strings in the set:
Determines if a string is in the set. This operation is identical to tries except that some edges consume multiple characters.
Add a string to the tree. We search the tree until we can make no further progress. At this point we either add a new outgoing edge labeled with all remaining characters in the input string, or if there is already an outgoing edge sharing a prefix with the remaining input string, we split it into two edges (the first labeled with the common prefix) and proceed. This splitting step ensures that no node has more children than there are possible string characters.
Delete a string from the tree. First, we delete the corresponding leaf. Then, if its parent only has one child remaining, we delete the parent and merge the two incident edges.
The array present in each node is of size 58 where the index corresponds to the alphabets in ASCII notation. This takes care of the sorting of keys.
In order to handle multithreading, pthread_mutex_locks are used. Whenever a particular funcitonality is being executed, the other two are prevented from accessing the database. For eg: if the put() API is called, then the get() and del() APIs are prevented from meddling with the database. This is achieved by having a total of 4 locks.
pthread_mutex_init(&del_lock, NULL);
pthread_mutex_init(&put_lock, NULL);
pthread_mutex_init(&get_lock, NULL);
pthread_mutex_init(&db_lock, NULL);The del_lock, put_lock, get_lock are for the respective API calls, while the db_lock is used to lock the database while testing takes place as well.
| Supported API | Desccription |
|---|---|
| get(key) | Returns the value of the key |
| put(key, value) | Adds key-value, and overwrites the existing value |
| delete(key) | Delete the key from the data-structure |
| get(int n) | Returns the value of lexographically nth smaller key |
| delete(int n) | Delete the nth key-value pair |
Slice struct is used for storing the key and the value of every KV pair. The value of key or value along with its length are the components of the struct. By default, as defined in the constructor, the size is equal to 0 and the data value is a null string.
Trie struct has:
- an array of Trie structs to store the children nodes,
- an integer variable for storing the number of end nodes at, or below that node,
- an boolean value which if true denotes that a Kv pair ends at that node,
- a string which stores the key ending at that node (if any) and
- a slice struct for storing the value associated with the key if the node is a terminal node.
When a new node is created in the radix trie, it has zero descendants and is defined to not be a end node. All the children node pointers are by default initialized to NULL.
Starting from the root node, recursivesly go down each layer and look for a key match with the key words terminating at that node under consideration. If matched and the node is a terminal node, we output True.
Add a string to the tree. We search the tree until we can make no further progress. At this point there are five possible cases,
Key to be inserted doesn't exist and had no common prefix in the database: In this case the key is simply inserted via a pointer from the root node.
Key to be inserted already exits.
Here the trie traversed to reach the last node of the key and the value is overwritten. While traversing the trie for this key the descendants are incremented due to a condition in the search function.
To correct this appropriate node descendant values are decremented.
The key to be inserted is a super string of a node present in the database
Here, the common prefix is left untouched and the remaining part is attached is node to this common prefix.
The key to be inserted is a substring of a node in the database.
Here, the existing is broken into the common prefix and the remaining part which is attached as child to the common prefix node.
The descendants of the new and existing nodes are updated appropriately.
The key to be inserted has a common prefix with an existing node in the trie.
Here, the uncommon part of the existing node is broken into a new node and the key is inserted as a whole. The uncommon part of the key is then broken into a new node and then attached to the common prefix. Now the existing uncommon node is also attached to the common prefix node.
All splitting steps ensure that no node has more children than there are possible string characters.
Search through the nodes and find out the node where the desired key terminates. If the parent of that node had only one other child, remove that parent node too and add the other node to the grand-parent node of the respective terminal nodes.
The SearchN function is used to find the key of the lexographcially Nth smallest key and the KV pair is removed from the radix trie using the TrieRemove function with the obtained key as a parameter.
Searching a trie T for a key w just requires tracing a path down the trie as follows: at depth i, the ith digit of w is used to orientate the branching. We need to specify which search structure is used to choose the correct sub-trie within a node.
Uses an array of pointers to sub-tries. In case of a large alphabet too many empty pointers are created.
Linked list of sub-tries reduces the high storage requirement of the array-trie hybrid but traversal operations are expensive.
Binary Search Trees have the time efficiency of arrays and the space efficiency of the linked lists.
1. The analysis of hybrid trie structures, Clément (Julien), Flajolet (Philippe), and Vallée (Brigitte).
2. Redesigning the String Hash Table, Burst Trie, and BST to Exploit Cache, Nikolas Askitis, and Justin Zobel
3. Emory CS323 Data Structures and Algorithms: Compressed(Patricia) Tries

