Nikita Smirnov BS18-RO
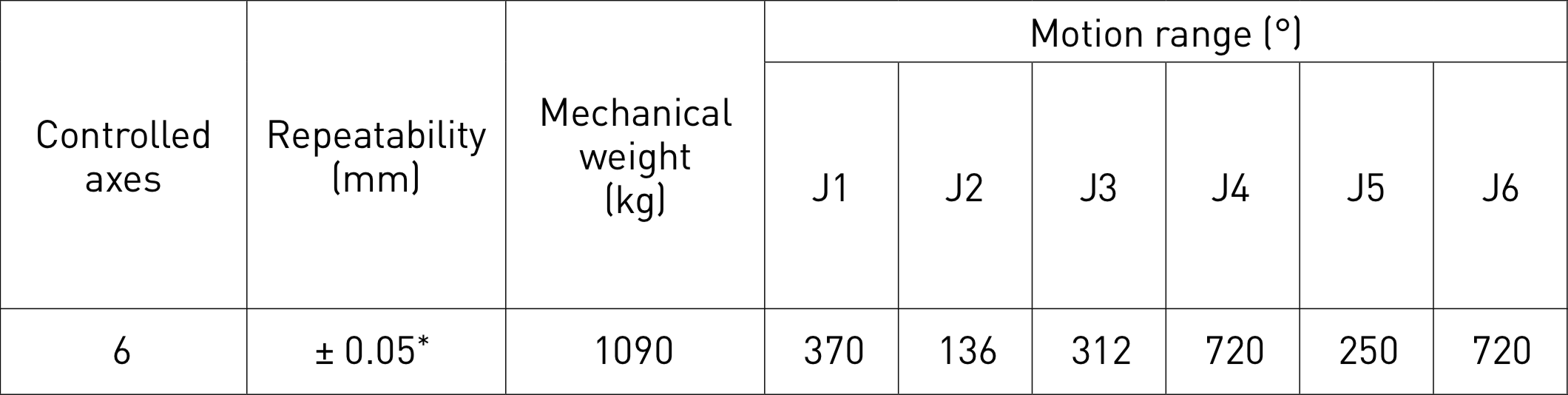
6 d.o.f
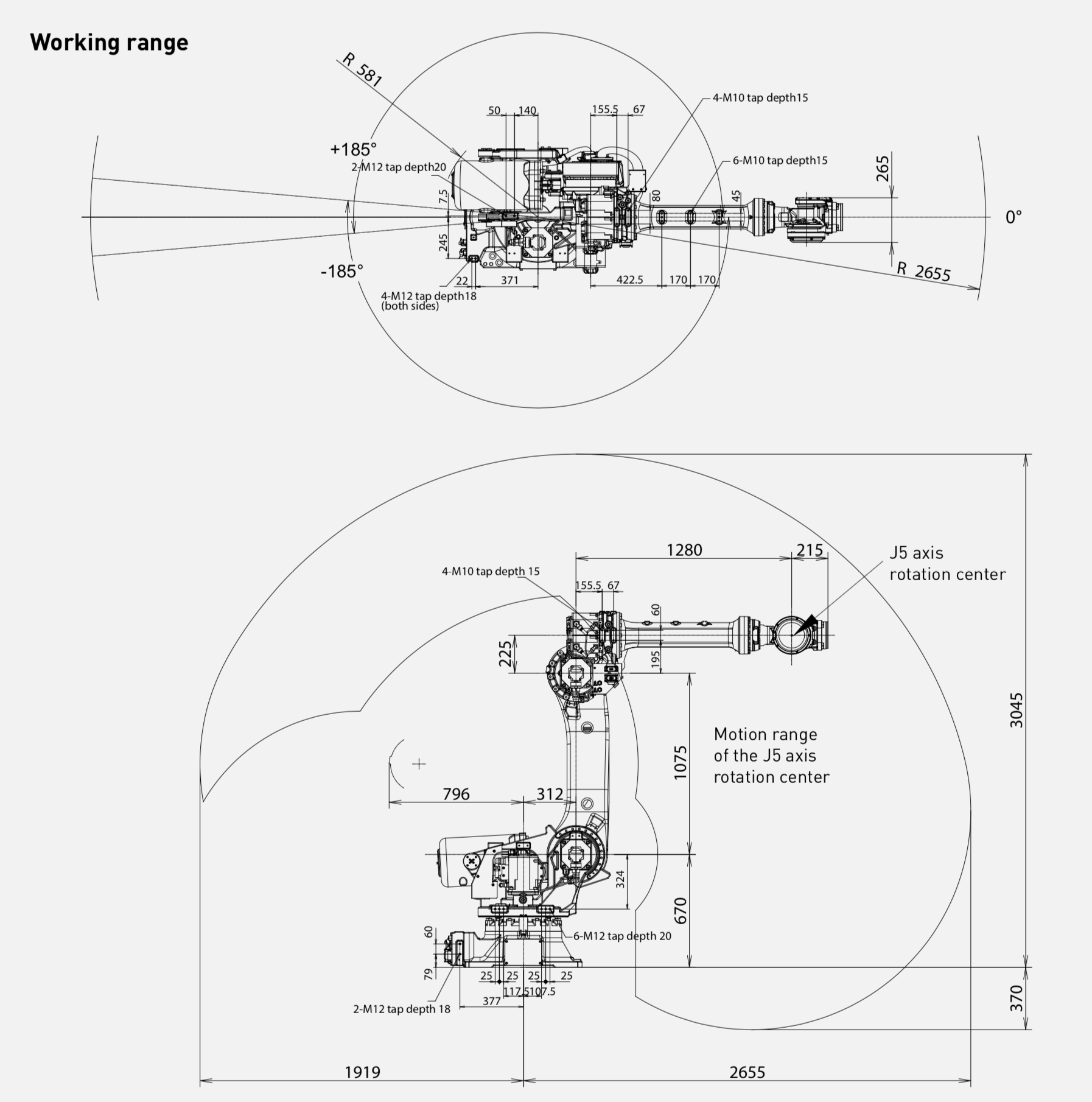
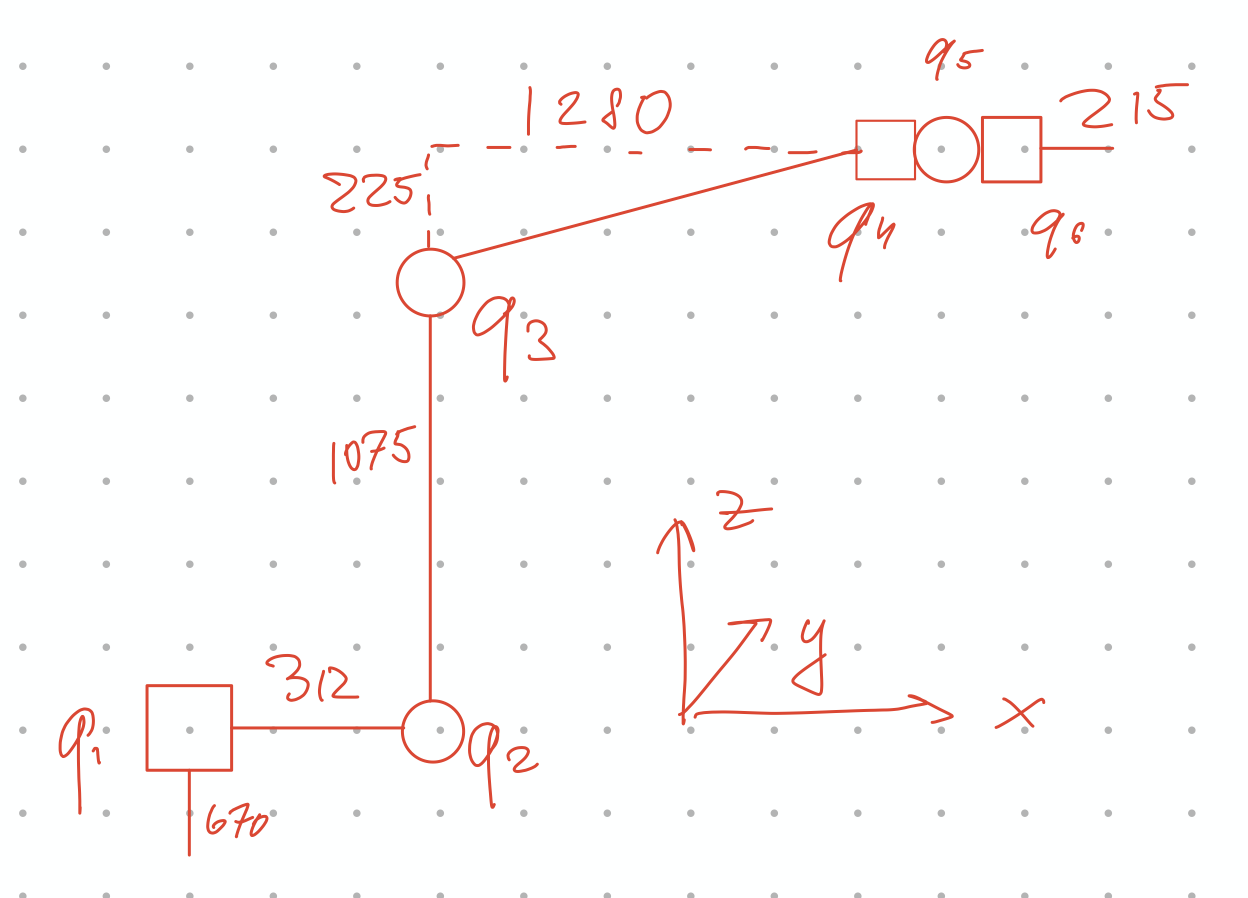
5 links (in schematic representation). Near each link (including 2 real links ) depicted their size.
6 joints. Last 3 joint can be represented as prizmatic joint or wrist.
3 angles (a1, a2, a3) and 3 coordinates (x, y, z).
To find angles: $$ a_1 = atan2(T_{23}, T_{33})\ if\ c2\ne 0 \ a_2 = atan2(-T_{13}, T_{11}|T_{12}) \ a_3 = atan2(T_{12}, T_{11}) \ if\ c2\ne 0 $$ Way to find coordinates is obvious
Using this we find q1, q2, q3 using geometrical method. $$ T_{123}^{-1}Tz(670)^{-1}\times T\times Tx^{-1}(215) = T_{456} $$ $$ T_{456} = \left( \begin{array}{cccc} \text{c5} & \text{s5} \text{s6} & -\text{c6} \text{s5} & 0 \ \text{s4} \text{s5} & \text{c4} \text{c6}-\text{c5} \text{s4} \text{s6} & \text{c4} \text{s6}+\text{c5} \text{c6} \text{s4} & 0 \ \text{c4} \text{s5} & -\text{c4} \text{c5} \text{s6}-\text{c6} \text{s4} & \text{c4} \text{c5} \text{c6}-\text{s4} \text{s6} & 0 \ 0 & 0 & 0 & 1 \ \end{array} \right) $$
Knowing this, I've applied algo similar to finding FK.