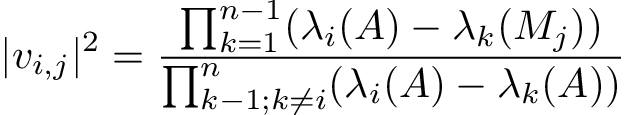This code generates a random Hermitian matrix of dimension n and then calculates the norm squared of the elements of the normed eigenvectors, |vi,j|2. It then verifies that the result is equivalent to that calculated with numpy. To use this code simply run the file as is to numerically verify the formula:
python E2.py
0.08307505701632452
0.08307505701632453
[[ True True True True True True True True]
[ True True True True True True True True]
[ True True True True True True True True]
[ True True True True True True True True]
[ True True True True True True True True]
[ True True True True True True True True]
[ True True True True True True True True]
[ True True True True True True True True]]
where the first two numbers are |v0,1|2 calculated with the new formula and numpy and the array is the comparison of each element of each eigenvector.
Alternatively, import it into your own code as:
import E2
E2.vijsq(H, i, j)
which returns the norm square of the jth element of the ith eigenvector where H is a Hermitian matrix of numpy's matrix class, and i and j are indices 0 ≤ i,j ≤ n.
The new formula is:
For further references see arXiv:1908.03795. We first discovered this in the context of neutrino oscillations in matter in arXiv:1907.02534. We believe that the first instance of anything like this expression appeared in Karl Löwner. Über monotone Matrixfunktionen. Math. Z., 38(1):177–216, 1934. The first instance of this expression seems to have appeared in R. C. Thompson. Principal submatrices of normal and Hermitian matrices. Illinois J. Math., 10:296–308, 1966. A related expression appeared in 1834 by Jacobi.