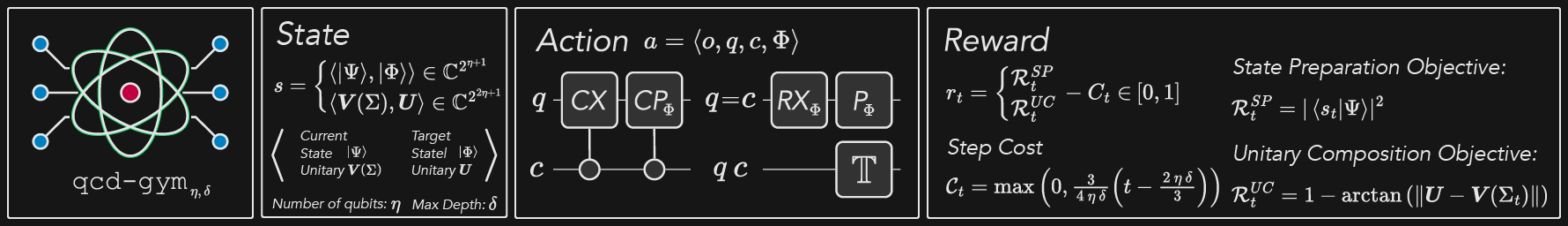Quantum Circuit Designer

Description

This repository contains qcd-gym, a generic gymnasium environment to build quantum circuits gate-by-gate using qiskit, revealing current challenges regarding:

• State Preparation (SP): Find a gate sequence that turns some initial state into the target quantum state.
• Unitary Composition (UC): Find a gate sequence that constructs an arbitrary quantum operator.

Observations

The observation is comprised of the state of the current circuit, represented by the full complex vector representation $\ket{\Psi}$ or the unitary operator $\boldsymbol{V}(\Sigma_t)$ resulting from the current sequence of operations $\Sigma_t$, as well as the intended target. While this information is only available in quantum circuit simulators efficiently (on real hardware, $\mathcal{O}(2^\eta)$ measurements would be needed), it depicts a starting point for RL from which future work should extract a sufficient, efficiently obtainable, subset of information. This state representation is sufficient for the definition of an MDP-compliant environment, as operations on this state are required to be reversible.

Actions

We use a $4$-dimensional Box action space $\langle o, q, c, \Phi \rangle = a \in \mathcal{A} = {\Gamma \times \Omega \times \Theta}$ with the following elements:

Name	Parameter	Type	Description
Operation	$o \in \Gamma$	int	specifying operation (see next table)
Qubit	$q \in[0, \eta)$	int	specifying qubit to apply the operation
Control	$c \in[0, \eta)$	int	specifying a control qubit
Parameter	$\Phi \in[- \pi,\pi]$	float	continuous parameter

The operations $\Gamma$ are defined as:

o	Operation	Condition	Type	Arguments	Comments
0	$\mathbb{Z}$	$q = c$	PhaseShift	$q,\Phi$	Control omitted
0	$\mathbb{Z}$	$q \neq c$	ControlledPhaseShift	$q,c,\Phi$	-
1	$\mathbb{X}$	$q = c$	X-Rotation	$q,\Phi$	Control omitted
1	$\mathbb{X}$	$q \neq c$	CNOT	$q,c$	Parameter omitted
2	$\mathbb{T}$		Terminate		All agruments omitted

With operations according to the following unversal gate set:

• CNOT: $$CX_{q,c} = \ket{0}\bra{0}\otimes I + \ket{1}\bra{1}\otimes X$$
• X-Rotation: $$RX(\Phi) = \exp\left(-i \frac{\Phi}{2} X\right)$$
• PhaseShift: $$P(\Phi) = \exp\left(i\frac{\Phi}{2}\right) \cdot \exp\left(-i\frac{\Phi}{2} Z\right)$$
• ControlledPhaseShift: $$CP(\Phi) = I \otimes \ket{0} \bra{0} + P(\Phi) \otimes \ket{1} \bra{1}$$

Reward

The reward is kept $0$ until the end of an episode is reached (either by truncation or termination). To incentivize the use of few operations, a step-cost $\mathcal{C}_t$ is applied when exceeding two-thirds of the available operations $\sigma$: $$\mathcal{C}_t=\max\left(0,\frac{3}{2\sigma}\left(t-\frac{\sigma}{3}\right)\right)$$

Suitable task reward functions $\mathcal{R}^{\ast}\in[0,1]$ are defined, s.t.: $\mathcal{R}=\mathcal{R}^{\ast}(s_t,a_t)-C_t$ if $t$ is terminal, according to the following objectives:

Objectives

State Preparation

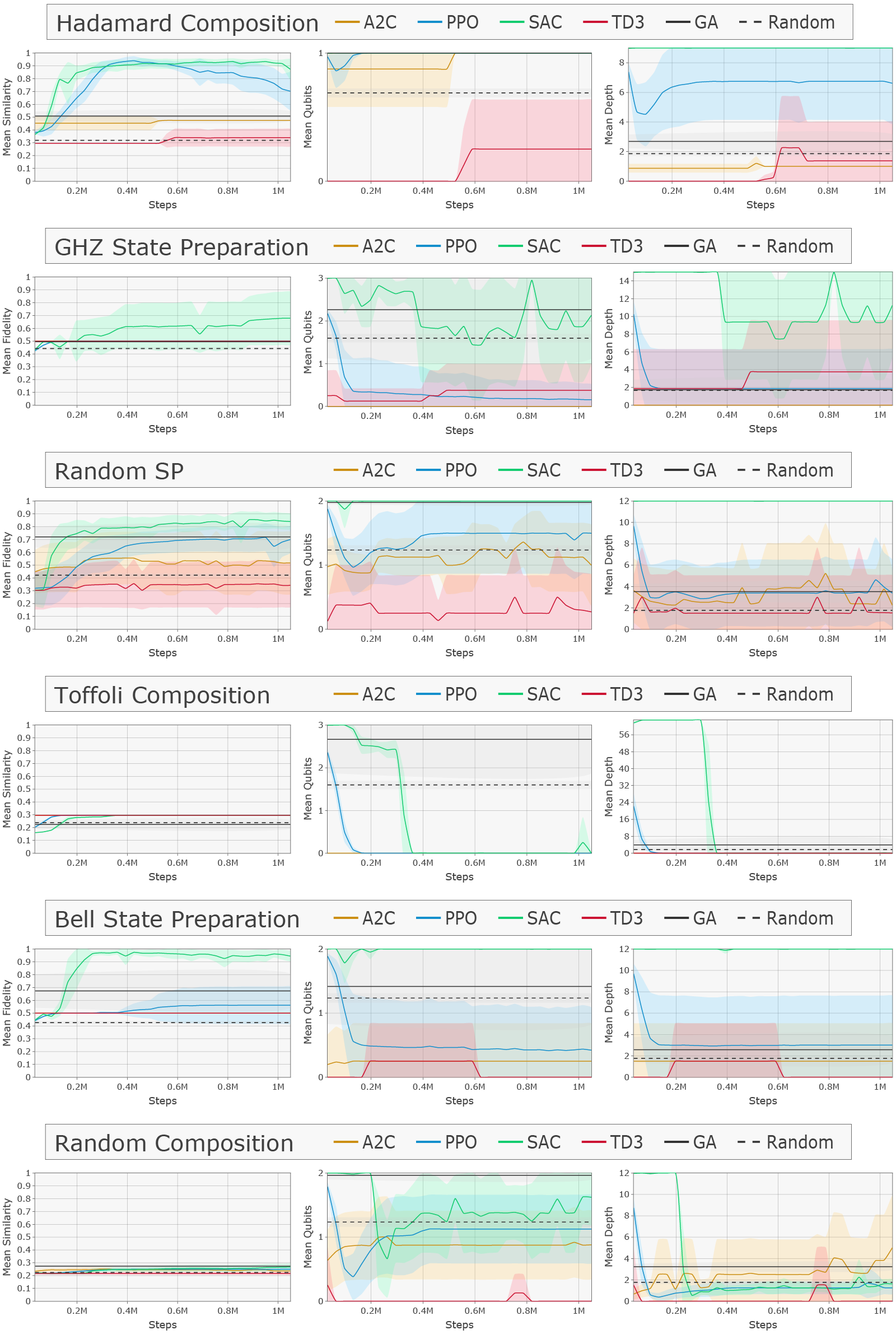
The task of this objective is to construct a quantum circuit that generates a desired quantum state. The reward is based on the fidelity between the target an the final state: $$\mathcal{R}^{SP}(s_t,a_t) = F(s_t, \Psi) = |\braket{\psi_{\text{env}}|\psi_{\text{target}}}|^2 \in [0,1]$$ Currently, the following states are defined:

• 'SP-random' (a random state over max_qubits )
• 'SP-bell' (the 2-qubit Bell state)
• 'SP-ghz<N>' (the <N> qubit GHZ state)

Unitary Composition

The task of this objective is to construct a quantum circuit that implements a desired unitary operation. The reward is based on the Frobenius norm $D = |U - V(\Sigma_t)|_2$ between the taget unitary $U$ and the final unitary $V$ based on the sequence of operations $\Sigma_t = \langle a_0, \dots, a_t \rangle$:

$$ R^{UC}(s_t,a_t) = 1 - \arctan (D)$$

The following unitaries are currently available for this objective:

• 'UC-random' (a random unitary operation on max_qubits )
• 'UC-hadamard' (the single qubit Hadamard gate)
• 'UC-toffoli' (the 3-qubit Toffoli gate)

Further Objectives

The goal of this implementation is to not only construct any circuit that fulfills a specific objective but to also make this circuit optimal, that is to give the environment further objectives, such as optimizing:

• Circuit Depth
• Qubit Count
• Gate Count
• Parameter Count
• Qubit-Connectivity

These circuit optimization objectives can be switched on by the parameter punish when initializing a new environment.

Currently, the only further objective implemented in this environment is the circuit depth, as this is one of the most important features to restrict for NISQ (noisy, intermediate-scale, quantum) devices. This metric already includes gate count and parameter count to some extent. However, further objectives can easily be added within the Reward class of this environment.

Setup

Install the quantum circuit designer environment

pip install qcd-gym

The environment can be set up as:

import gymnasium as gym

env = gym.make("CircuitDesigner-v0", max_qubits=2, max_depth=10, objective='SP-bell', render_mode='text')
observation, info = env.reset(seed=42); env.action_space.seed(42)

for _ in range(9):
  action = env.action_space.sample()  # this is where you would insert your policy
  observation, reward, terminated, truncated, info = env.step(action)
  if terminated or truncated: observation, info = env.reset()

env.close()

The relevant parameters for setting up the environment are:

Parameter	Type	Explanation
max_qubits $\eta$	int	maximal number of qubits available
max_depth $\delta$	int	maximal circuit depth allowed (= truncation criterion)
objective	str	RL objective for which the circuit is to be built (see Objectives)
punish	bool	specifier for turning on multi-objectives (see Further Objectives)

Running benchmarks

Running benchmark experiments requires a full installation including baseline algorithms extending stable_baselines3 and a plotting framework extending plotly: This can be achieved by:

git clone https://github.com/philippaltmann/QCD.git
pip install -e '.[all]'

Specify the intended <Task> as: "objective-qmax_qubits-dmax_depth":

# Run a specific algoritm and task (requires `pip install -e '.[train]'`)
python -m train [A2C | PPO | SAC | TD3] -e <Task>

# Generate plots from the `results` folder (requires `pip install -e '.[plot]'`) 
python -m plot results -b # plot all runs in `results`, add random and evo baselines

# To train the provided baseline algorithms, use (pip install -e .[all])
./run.sh

# Test the circuit designer (requires `pip install -e '.[test]'`)
python -m test

Results

Acknowledgements

The research is part of the Munich Quantum Valley, which is supported by the Bavarian state government with funds from the Hightech Agenda Bayern Plus.