Generic goodness of fit tests for random plain old data.
Goftests is intended for unit testing random samplers that generate arbitrary plain-old-data, and focuses on robustness rather than statistical efficiency. In contrast to scipy.stats and statsmodels, goftests does not make assumptions on the distribution being tested, and requires only a simple (sample, prob) interface provided by MCMC samplers.
pip install goftests
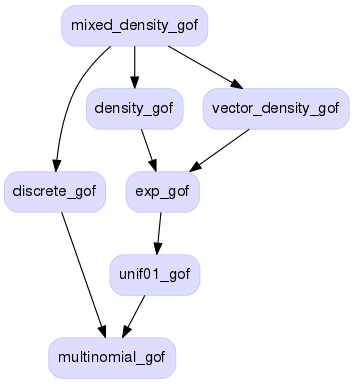
Goftests implements generic statistical tests for Monte Carlo samplers that generate (sample, probability) pairs. The four basic generic tests are
-
discrete_goodness_of_fit(samples, probs_dict, ...)- for discrete-valued data with most of the mass on a few values. -
density_goodness_of_fit(samples, probs, ...)- for continuously distributed univariate data with no discrete component. -
vector_density_goodness_of_fit(samples, probs, ...)- for continuously distributed multivariate data with no discrete component. -
mixed_density_goodness_of_fit(samples, probs, ...)- for discretely-indexed continuously distributed data, subsuming the all the other tests.
Each test outputs a goodness of fit number, say gof,
which should be uniformly distributed in the interval [0,1],
and which tends to fail with numbers close to zero.
Thus to test a sampler we usually write
TEST_FAILURE_RATE = 1e-3
def test_my_sampler(count=100):
seed_all(0)
samples = [my_sampler.rvs() for _ in xrange(count)]
probs = [my_sampler.pdf(x) for x in samples]
gof = mixed_density_goodness_of_fit(samples, probs)
assert gof > TEST_FAILURE_RATE
By specifying a global TEST_FAILURE_RATE for a suite of tests,
we can tune the number of tests expected to fail.
In a large suite of tests, some may fail at the specified seeds despite the distribution being correct, typically with gof just below the threshold.
In this case we usually increment the seed on those tests.
In a suite of 1000 tests with TEST_FAILURE_RATE = 1e-3,
we should expect to have to increment the seed on 1 test, on average.
The discrete tests only look at the most-likely few values, and requires enough samples in the top few values to be able to use Pearson's χ2 test. This is typically at least 100 samples.
The univariate tests require around 100 samples, and the multivariate require at least 1000 per dimension.
When testing for millions of samples or more, tests can fail due to numeric imprecision rather than poor distribution. We have had success testing with 102-105 samples.
When testing samples generated by MCMC, the samples are often correlated so that testing the entire chain fails. In this case, try running the chain for longer and subsampling only every kth step in the chain.
The density tests are sensitive to Sticky Markov chains. As with poorly mixing chains, try running for longer.
Be sure to set a deterministic seed via seed_all(...)
before generating each dataset.
In particular, some test runners run tests in a nondeterministic order,
so setting the seed before generating each sample ensures deterministic behavior.
The goodness of fit tests are mostly implemented by reduction to other tests, eventually reducing to the multinomial goodness of fit test which uses Pearson's χ2 test on each of the multinomial's bins.
To implement a new test, you can implement from scratch, reduce to another test in goftests, or reduce to standard tests in another package like scipy.stats or statsmodels.
-
[1] <name=1> Peter J Bickel, Leo Breiman (1983) "Sums of functions of nearest neighbor distancess, moment bounds, limit theorems and a goodness of fit test" pdf
-
[2] <name=2> Mike Williams (2010) "How good are your fits? Unbinned multivariate goodness-of-fit tests in high energy physics" pdf
Copyright (c) 2014 Salesforce.com, Inc. All rights reserved.
Copyright (c) 2015 Gamelan Labs, Inc.
Copyright (c) 2016 Google, Inc.
Copyright (c) 2019 Gamalon, Inc.
Licensed under the Revised BSD License.
See LICENSE.txt for details.