Skip to content

Latest commit

 

History

History
227 lines (176 loc) · 7.96 KB

README.de.md

File metadata and controls

227 lines (176 loc) · 7.96 KB

Adjoint Logo

Kenntnisfreier Protokoll

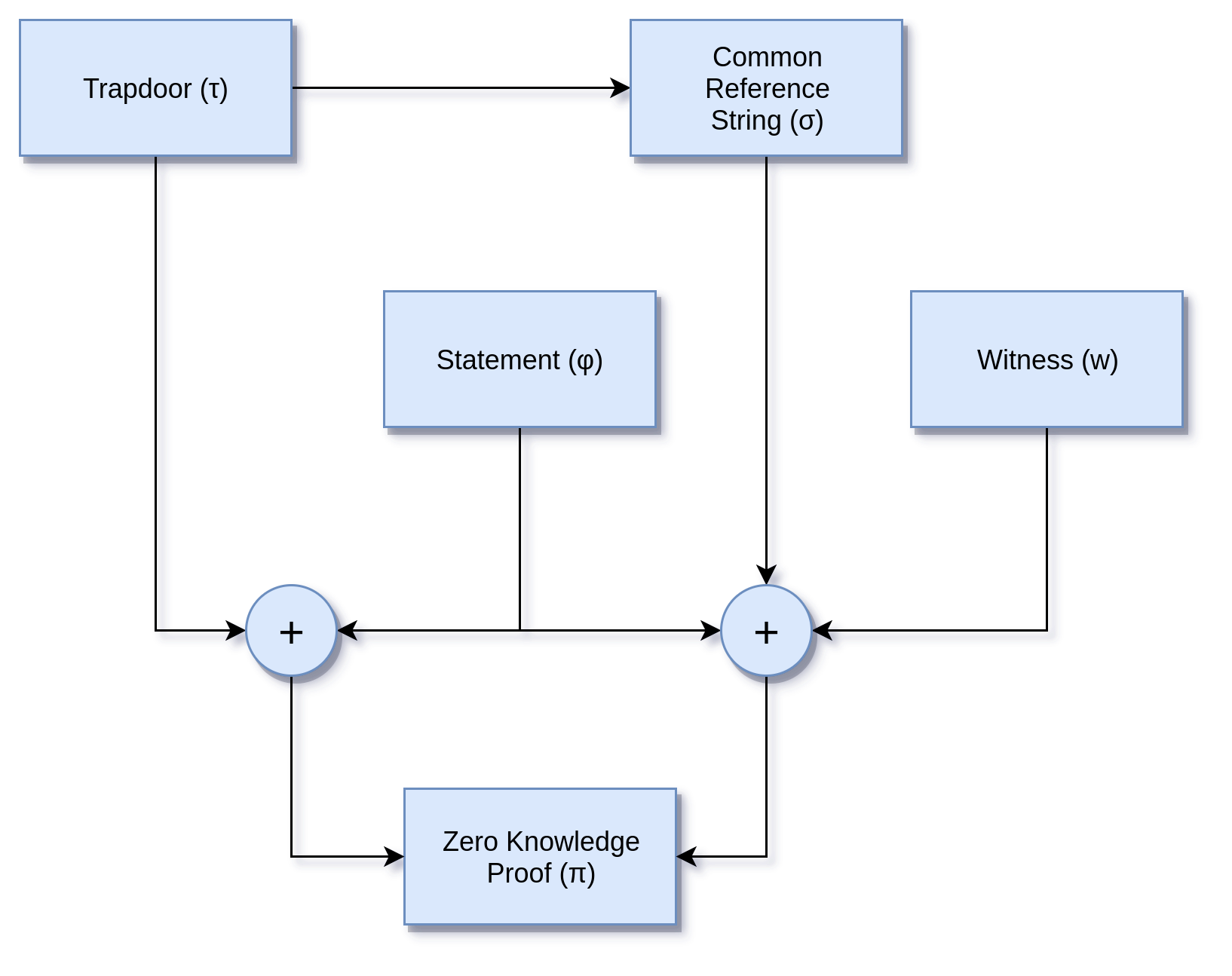
ZKP ist ein praktisches kenntnisfreies Protokoll, das kleine und recheneffiziente Zero-Knowledge-Proofs für beliebige Berechnungen bereitstellt. Mit diesem System können wir kurze, nicht interaktive Proofs mit günstigen und schnellen Überprüfungszeiten erstellen. Die Topologie des Proof-Generierungssystems wird in der folgenden Abbildung beschrieben.

Groth16

Compiler-Stufen

  • Programmaufbau
  • Vertrauenswürdiges Setup
  • Proof-Generierung
  • Nachweisprüfung

Programmentwicklung

Die Programmkonstruktion wird von anderen Bibliotheken entwickelt, die einen Standard-JSON ausgeben Protokoll, das die funktionale Zusammensetzung von arithmetisch berechneten Toren beschreibt Operationen der Addition und Multiplikation und mit Drähten. Diese Bibliothek kann Verwenden Sie einfach einen anderen Compiler oder eine andere Bibliothek, die JSON als Austausch ausgibt Format.

Eine Referenzbibliothek für die Schaltungskonstruktionssprache wird von bereitgestellt Rechenschaltungen Paket.

Vertrauenswürdiges Setup

Das vertrauenswürdige Setup kann über die Befehlszeile ausgeführt werden. Welches wird die eine erzeugen Zeitparameter, die für die Einrichtung eines bestimmten Stromkreises benötigt werden. Die Setup-Parameter können entweder später zerstört oder in einem geheimen Shamir-Sharing verteilt werden Aufbau. Die Shamir-Freigabe ermöglicht ein n-von-m-Setup mit einem Minimum von n Die Teilnehmer müssen ihre geheimen Teile kombinieren, um das vertrauenswürdige Setup wiederherzustellen.

zkp setup --prover Groth16 --input samples/example1.json -o setupdir

Dadurch werden die vertrauenswürdigen Setup-Parameter im Verzeichnis "setupdir" generiert. Diese fünf Zufallsparameter (α,β,𝛾,δ,x) aus dem Primfeld Fr der elliptischen Kurve BN254

RandomSetup
  { setupAlpha =
      P 12256559805687004284032990640481138455228350420895296477627313054450750333538
  , setupBeta =
      P 4401553107086663101145669242467980542018664489189708849056812824771109996937
  , setupGamma =
      P 11751086019938025633396747311851452921508835627313304853903993116945166687533
  , setupDelta =
      P 168604024821165987426171350616143663866971217710026689954359697680025921731
  , setupX =
      P 17090290750981977232640417368259094286138615605287635462955897488010126230557
  }

Wenn Sie Hardware-Entropie aus dem Kernel verwenden möchten, um den Zufall auszuführen Generation übergeben die --hardware Flagge während des Trusted Setups.

Beweiserstellung

Für einen gegebenen Satz gültiger Eingaben ( --inputs) wird hierdurch der Proof generiert Ausdruck pi in eine Proof-Datei. Dies beinhaltet den prägnanten Null-Wissensnachweis die Auswertung der Schaltung mit den vorgegebenen vertrauenswürdigen Setup- und Programmeingaben.

zkp prove --input samples/example1.json -d setupdir --inputs samples/inputs1.json --pi proof

Dies wird einen π - Beweisbegriff erzeugen, der aus drei Begriffen in besteht aus der bilinearen Abbildung A : G2, B : G1 and C : G1.

Proof
  { proofA =
      A (P 4881623700312852323508547682818174690864977127565225101692969747455865314076)
        (P 21226270279582811012422188678741405568697460494611910557066940647978844558004)
  , proofB =
      A (E (P 20323099801991325872207033941577805160427313780137510282152872074461606067272 *
              X +
              P 1422252355533785307633747654423585463232482725315893764382065912760224949248))
        (E (P 3567658277931205602889970963406800124094834788390622140804820116722346374274 *
              X +
              P 15030027696371368845331628915595104373945089162840261486371773861661834388966))
  , proofC =
      A (P 21113978983642622273905001525315900726975017023639887701995527379031005434733)
        (P 1703880359115562486637532379447225273456712398817044635461020607254025768226)
  }

Nachweisprüfung

Der Verifizierungsalgorithmus verwendet als Eingabe eine eingeschränkte gemeinsame Referenzzeichenfolge und ein Beweisbegriff ( --pi) berechnet die endgültige Paarungsoperation, um das zu verifizieren Integrität des Proofs und gibt eine Ablehnung oder eine Annahme als Exit-Code zurück.

zkp verify -d setupdir --inputs samples/inputs1.json --pi proof

Kurven

Dieses Beweissystem verwendet eine polymorphe Darstellung der elliptischen Kurve Operationen, mit denen wir den Beweiser über mehrere elliptische Kurven instanziieren können einschließlich:

  • BN254
  • BLS12-381

Aus der Quelle bauen

Diese Bibliothek wird auf 8.x des Haskell-Compilers kompiliert. Zum Installieren von GHC verwenden Sie ghcup.

ghcup install 8.6.5

Laden Sie diese Bibliothek nach der Einrichtung von GHC herunter und erstellen Sie sie mit cabal.

git clone [email protected]:adjoint-io/zkp.git
cd zkp
cabal new-install --installdir=.
cp ./zkp ~/.local/bin

Alternativ kann diese Bibliothek mit erstellt werden stack:

cd zkp
stack install

Docker Images

Die ausführbare Datei zkp kann in einem Docker-Image erstellt und ausgeführt werden:

$ docker build -t zkp .
$ docker run -ti zkp /bin/bash

Verifikation

Dies ist ein optionaler Schritt und nur für Entwickler.

ZKP wird mit einer Reihe von Spezifikationen durch Verfeinerungsarten angereichert, die sind überprüfbar die LiquidHaskell Rahmen. LiquidHaskell analysiert die Module und erfüllt die Nachweispflichten zu einem SMT-Löser, um zu sehen, ob die Bedingungen erfüllt sind. Dies ermöglicht es uns, beweisen das Fehlen einer Familie von Fehlern in Bezug auf Speichersicherheit, Arithmetik Ausnahmen und Informationsfluss.

Sie benötigen entweder Microsoft Research Z3 SMT Solver oder Stanford CVC4 SMT Solver.

Für Linux:

sudo apt install z3 # z3
sudo apt install cvc4 # cvc4

Für Mac:

brew tap z3 # z3
brew tap cvc4/cvc4 # cvc4
brew install cvc4/cvc4/cvc4

Dann installieren Sie LiquidHaskell entweder mit Cabal oder Stack:

cabal install liquidhaskell
stack install liquidhaskell

Die Überprüfung kann dann über die Kryptografiemodule in diesem Projekt ausgeführt werden.

liquid -f --cabaldir -i src -i spec src/Poly.hs
liquid -f --cabaldir -i src -i spec src/Protocol/Groth.hs

Abhängigkeiten

Dieses Beweissystem hängt von den folgenden Abhängigkeiten ab.