The following collection of materials targets "Physics-Based Deep Learning" (PBDL), i.e., the field of methods with combinations of physical modeling and deep learning (DL) techniques. Here, DL will typically refer to methods based on artificial neural networks. The general direction of PBDL represents a very active and quickly growing field of research.
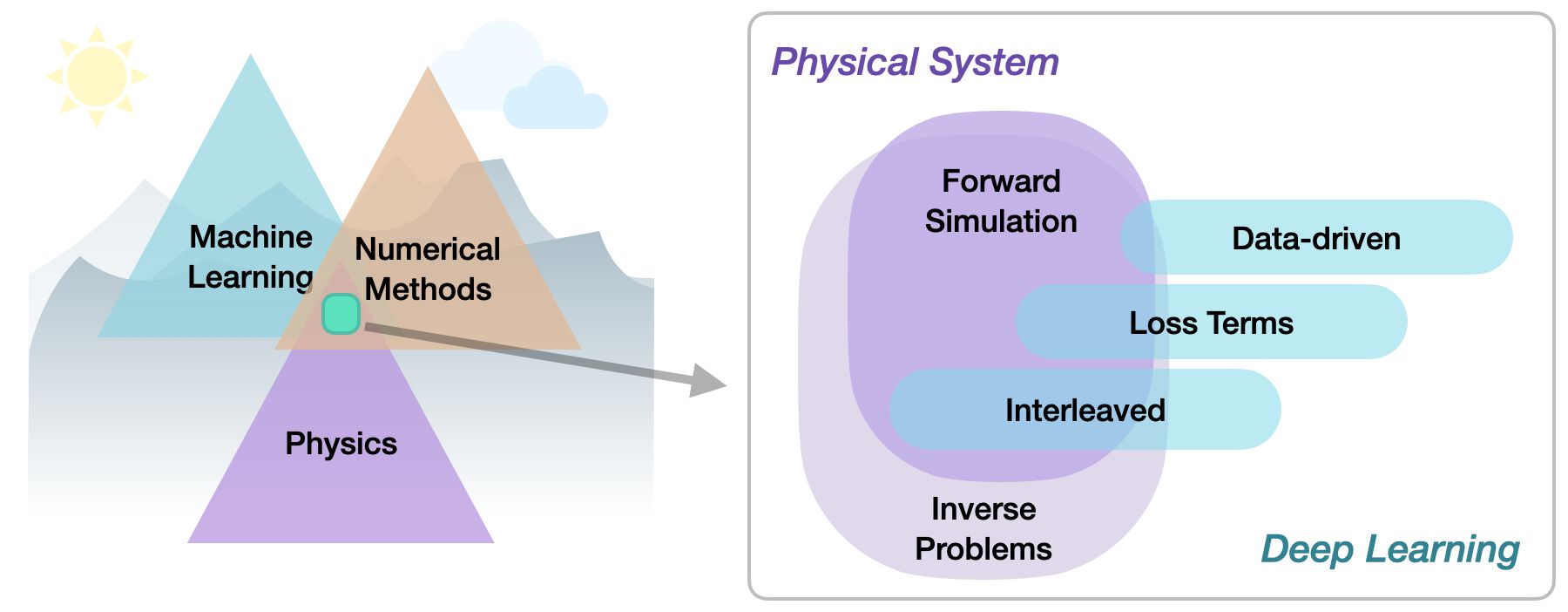
Within this area, we can distinguish a variety of different physics-based approaches, from targeting designs, constraints, combined methods, and optimizations to applications. More specifically, all approaches either target forward simulations (predicting state or temporal evolution) or inverse problems (e.g., obtaining a parametrization for a physical system from observations). Apart from forward or inverse, the type of integration between learning and physics gives a means for categorizing different methods:
-
Data-driven: the data is produced by a physical system (real or simulated), but no further interaction exists.
-
Loss-terms: the physical dynamics (or parts thereof) are encoded in the loss function, typically in the form of differentiable operations. The learning process can repeatedly evaluate the loss, and usually receives gradients from a PDE-based formulation.
-
Interleaved: the full physical simulation is interleaved and combined with an output from a deep neural network; this requires a fully differentiable simulator and represents the tightest coupling between the physical system and the learning process. Interleaved approaches are especially important for temporal evolutions, where they can yield an estimate of future behavior of the dynamics.
Thus, methods can be roughly categorized in terms of forward versus inverse solve, and how tightly the physical model is integrated into the optimization loop that trains the deep neural network. Here, especially approaches that leverage differentiable physics allow for a tighter and tighter integration of deep learning and numerical simulations.
This repository collects links to works on deep learning algorithms for physics problems, with a particular emphasis on fluid flow, i.e., Navier-Stokes related problems. It primarily collects links to the work of the I15 lab at TUM, as well as miscellaneous works from other groups. This is by no means a complete list, so let us know if you come across additional papers in this area. We intentionally also focus on works from the deep learning field, not machine learning in general.
Solver-in-the-Loop: Learning from Differentiable Physics to Interact with Iterative PDE-Solvers , Project+Code: https://ge.in.tum.de/publications/2020-um-solver-in-the-loop/
Numerical investigation of minimum drag profiles in laminar flow using deep learning surrogates , PDF: https://arxiv.org/pdf/2009.14339
Purely data-driven medium-range weather forecasting achieves comparable skill to physical models at similar resolution , PDF: https://arxiv.org/pdf/2008.08626
Data-driven Regularization via Racecar Training for Generalizing Neural Networks , PDF: https://arxiv.org/pdf/2007.00024
Latent Space Subdivision: Stable and Controllable Time Predictions for Fluid Flow , PDF: https://arxiv.org/pdf/2003.08723
WeatherBench: A benchmark dataset for data-driven weather forecasting , Project: https://github.com/pangeo-data/WeatherBench
Learning Similarity Metrics for Numerical Simulations (LSiM) , Project+Code: https://ge.in.tum.de/publications/2020-lsim-kohl/
Learning to Control PDEs with Differentiable Physics , Project+Code: https://ge.in.tum.de/publications/2020-iclr-holl/
Lagrangian Fluid Simulation with Continuous Convolutions , PDF: https://openreview.net/forum?id=B1lDoJSYDH
Tranquil-Clouds: Neural Networks for Learning Temporally Coherent Features in Point Clouds , Project+Code: https://ge.in.tum.de/publications/2020-iclr-prantl/
ScalarFlow: A Large-Scale Volumetric Data Set of Real-world Scalar Transport Flows for Computer Animation and Machine Learning , Project+Code: https://ge.in.tum.de/publications/2019-tog-eckert/
tempoGAN: A Temporally Coherent, Volumetric GAN for Super-resolution Fluid Flow , Project+Code: https://ge.in.tum.de/publications/tempogan/
Deep Fluids: A Generative Network for Parameterized Fluid Simulations , Project+Code: http://www.byungsoo.me/project/deep-fluids/
Latent-space Physics: Towards Learning the Temporal Evolution of Fluid Flow , Project+Code: https://ge.in.tum.de/publications/latent-space-physics/
A Multi-Pass GAN for Fluid Flow Super-Resolution , PDF: https://ge.in.tum.de/publications/2019-multi-pass-gan/
A Study of Deep Learning Methods for Reynolds-Averaged Navier-Stokes Simulations , Project+Code: https://github.com/thunil/Deep-Flow-Prediction
Data-Driven Synthesis of Smoke Flows with CNN-based Feature Descriptors , Project+Code: http://ge.in.tum.de/publications/2017-sig-chu/
Liquid Splash Modeling with Neural Networks , Project+Code: https://ge.in.tum.de/publications/2018-mlflip-um/
Generating Liquid Simulations with Deformation-aware Neural Networks , Project+Code: https://ge.in.tum.de/publications/2017-prantl-defonn/
Super-resolution and denoising of fluid flow using physics-informed convolutional neural networks without high-resolution labels , PDF: https://arxiv.org/pdf/2011.02364.pdf
A Point-Cloud Deep Learning Framework for Prediction of Fluid Flow Fields on Irregular Geometries , PDF: https://arxiv.org/pdf/2010.09469
Learning Mesh-Based Simulations with Graph Networks , PDF: https://arxiv.org/pdf/2010.03409
Using Machine Learning to Augment Coarse-Grid Computational Fluid Dynamics Simulations , PDF: https://arxiv.org/pdf/2010.00072
Learning to swim in potential flow , PDF: https://arxiv.org/pdf/2009.14280
Enhanced data efficiency using deep neural networks and Gaussian processes for aerodynamic design optimization , PDF: https://arxiv.org/pdf/2008.06731
Learned discretizations for passive scalar advection in a 2-D turbulent flow , PDF: https://arxiv.org/pdf/2004.05477
Combining Differentiable PDE Solvers and Graph Neural Networks for Fluid Flow Prediction , PDF: https://proceedings.icml.cc/static/paper_files/icml/2020/6414-Paper.pdf
CFDNet: A deep learning-based accelerator for fluid simulations , PDF: https://arxiv.org/pdf/2005.04485
Controlling Rayleigh-Benard convection via Reinforcement Learning , PDF: https://arxiv.org/pdf/2003.14358
Embedding Hard Physical Constraints in Neural Network Coarse-Graining of 3D Turbulence , PDF: https://arxiv.org/pdf/2002.00021
Learning to Simulate Complex Physics with Graph Networks , PDF: https://arxiv.org/pdf/2002.09405
DPM: A deep learning PDE augmentation method (with application to large-eddy simulation) , PDF: https://arxiv.org/pdf/1911.09145
Towards Physics-informed Deep Learning for Turbulent Flow Prediction , PDF: https://arxiv.org/pdf/1911.08655
DeepFlow: History Matching in the Space of Deep Generative Models , PDF: https://arxiv.org/pdf/1905.05749
Deep learning observables in computational fluid dynamics , PDF: https://arxiv.org/pdf/1903.03040
Compressed convolutional LSTM: An efficient deep learning framework to model high fidelity 3D turbulence , PDF: https://arxiv.org/pdf/1903.00033
Deep neural networks for data-driven LES closure models , PDF: https://www.sciencedirect.com/science/article/pii/S0021999119306151
Dynamic Upsampling of Smoke through Dictionary-based Learning , PDF: https://arxiv.org/pdf/1910.09166
Deep unsupervised learning of turbulence for inflow generation at various Reynolds numbers , PDF: https://arxiv.org/pdf/1908.10515
Computing interface curvature from volume fractions: A machine learning approach , PDF: https://www.sciencedirect.com/science/article/abs/pii/S0045793019302282
Deep Neural Networks for Data-Driven Turbulence Models , PDF: https://export.arxiv.org/pdf/1806.04482
Deep Dynamical Modeling and Control of Unsteady Fluid Flows , PDF: http://papers.nips.cc/paper/8138-deep-dynamical-modeling-and-control-of-unsteady-fluid-flows
Learning Particle Dynamics for Manipulating Rigid Bodies, Deformable Objects, and Fluids , Project+Code: http://dpi.csail.mit.edu
Application of Convolutional Neural Network to Predict Airfoil Lift Coefficient , PDF: https://arxiv.org/pdf/1712.10082
Prediction of laminar vortex shedding over a cylinder using deep learning , PDF: https://arxiv.org/pdf/1712.07854
Lat-Net: Compressing Lattice Boltzmann Flow Simulations using Deep Neural Networks , PDF: https://arxiv.org/pdf/1705.09036
Reasoning About Liquids via Closed-Loop Simulation , PDF: https://arxiv.org/pdf/1703.01656
Prediction model of velocity field around circular cylinder over various Reynolds numbers by fusion convolutional neural networks based on pressure on the cylinder , PDF: https://doi.org/10.1063/1.5024595
Accelerating Eulerian Fluid Simulation With Convolutional Networks , Project+Code: https://cims.nyu.edu/~schlacht/CNNFluids.htm
Reynolds averaged turbulence modelling using deep neural networks with embedded invariance , PDF: https://www.labxing.com/files/lab_publications/2259-1524535041-QiPuSd6O.pdf
Aphynity: Augmenting physical models with deep networks for complex dynamics forecasting , PDF: https://arxiv.org/pdf/2010.04456.pdf
Hierarchical Deep Learning of Multiscale Differential Equation Time-Steppers , PDF: https://arxiv.org/pdf/2008.09768
Learning Compositional Koopman Operators for Model-Based Control , Project: http://koopman.csail.mit.edu
Universal Differential Equations for Scientific Machine Learning , PDF: https://arxiv.org/pdf/2001.04385.pdf
Understanding and mitigating gradient pathologies in physics-informed neural networks , PDF: https://arxiv.org/pdf/2001.04536
Variational Physics-Informed Neural Networks For Solving Partial Differential Equations , PDF: https://arxiv.org/pdf/1912.00873
Poisson CNN: Convolutional Neural Networks for the Solution of the Poisson Equation with Varying Meshes and Dirichlet Boundary Conditions , PDF: https://arxiv.org/pdf/1910.08613
IDENT: Identifying Differential Equations with Numerical Time evolution , PDF: https://arxiv.org/pdf/1904.03538
PDE-Net 2.0: Learning PDEs from Data with A Numeric-Symbolic Hybrid Deep Network , PDF: https://arxiv.org/pdf/1812.04426
Data-driven discretization: a method for systematic coarse graining of partial differential equations , PDF: https://arxiv.org/pdf/1808.04930
Solving high-dimensional partial differential equations using deep learning , PDF: https://www.pnas.org/content/115/34/8505.full.pdf
Neural Ordinary Differential Equations , PDF: https://arxiv.org/pdf/1806.07366
Deep Learning the Physics of Transport Phenomena , PDF: https://arxiv.org/pdf/1709.02432
DGM: A deep learning algorithm for solving partial differential equations , PDF: https://arxiv.org/pdf/1708.07469
Hidden Physics Models: Machine Learning of Nonlinear Partial Differential Equations , PDF: https://arxiv.org/pdf/1708.00588
Data-assisted reduced-order modeling of extreme events in complex dynamical systems , Project+Code: https://github.com/zhong1wan/data-assisted
PDE-Net: Learning PDEs from Data , Project+Code: https://github.com/ZichaoLong/PDE-Net
Learning Deep Neural Network Representations for Koopman Operators of Nonlinear Dynamical Systems , PDF: https://arxiv.org/pdf/1708.06850
Deep Energy-based Modeling of Discrete-Time Physics , PDF: https://proceedings.neurips.cc/paper/2020/file/98b418276d571e623651fc1d471c7811-Paper.pdf
NeuralSim: Augmenting Differentiable Simulators with Neural Networks , PDF: https://arxiv.org/pdf/2011.04217.pdf
Fourier Neural Operator for Parametric Partial Differential Equations , PDF: https://arxiv.org/pdf/2010.08895.pdf
Learning Composable Energy Surrogates for PDE Order Reduction , PDF: https://arxiv.org/pdf/2005.06549.pdf
Transformers for Modeling Physical Systems , PDF: https://arxiv.org/pdf/2010.03957
Reinforcement Learning for Molecular Design Guided by Quantum Mechanics , PDF: https://proceedings.icml.cc/static/paper_files/icml/2020/1323-Paper.pdf
Scalable Differentiable Physics for Learning and Control , PDF: https://proceedings.icml.cc/static/paper_files/icml/2020/15-Paper.pdf
Cloth in the Wind: A Case Study of Physical Measurement through Simulation , PDF: https://arxiv.org/pdf/2003.05065
Learning to Slide Unknown Objects with Differentiable Physics Simulations , PDF: https://arxiv.org/pdf/2005.05456
Physics-aware Difference Graph Networks for Sparsely-Observed Dynamics , Project: https://github.com/USC-Melady/ICLR2020-PADGN
Differentiable Molecular Simulations for Control and Learning , PDF: https://arxiv.org/pdf/2003.00868
Incorporating Symmetry into Deep Dynamics Models for Improved Generalization , PDF: https://arxiv.org/pdf/2002.03061
Learning to Measure the Static Friction Coefficient in Cloth Contact , PDF: https://hal.inria.fr/hal-02511646
Learning to Simulate Complex Physics with Graph Networks , PDF: https://arxiv.org/pdf/2002.09405
Hamiltonian Neural Networks , PDF: http://papers.nips.cc/paper/9672-hamiltonian-neural-networks.pdf
Interactive Differentiable Simulation , PDF: https://arxiv.org/pdf/1905.10706
DiffTaichi: Differentiable Programming for Physical Simulation , PDF: https://arxiv.org/pdf/1910.00935
COPHY: Counterfactual Learning of Physical Dynamics , Project: https://github.com/fabienbaradel/cophy
Modeling Expectation Violation in Intuitive Physics with Coarse Probabilistic Object Representations , Project: http://physadept.csail.mit.edu
End-to-End Differentiable Physics for Learning and Control , Project+Code: https://github.com/locuslab/lcp-physics
Stochastic seismic waveform inversion using generative adversarial networks as a geological prior , PDF: https://arxiv.org/pdf/1806.03720
Learning to Optimize Multigrid PDE Solvers , PDF: http://proceedings.mlr.press/v97/greenfeld19a/greenfeld19a.pdf
Latent-space Dynamics for Reduced Deformable Simulation , Project+Code: http://www.dgp.toronto.edu/projects/latent-space-dynamics/
Learning-Based Animation of Clothing for Virtual Try-On , PDF: http://www.gmrv.es/Publications/2019/SOC19/
Deep Lagrangian Networks: Using Physics as Model Prior for Deep Learning , PDF: https://openreview.net/pdf?id=BklHpjCqKm
Flexible Neural Representation for Physics Prediction , Project+Code: https://neuroailab.github.io/physics/
Robust Reference Frame Extraction from Unsteady 2D Vector Fields with Convolutional Neural Networks , PDF: https://arxiv.org/pdf/1903.10255
Physics-as-Inverse-Graphics: Joint Unsupervised Learning of Objects and Physics from Video , PDF: https://arxiv.org/pdf/1905.11169
Unsupervised Intuitive Physics from Past Experiences , PDF: https://arxiv.org/pdf/1905.10793
Reasoning About Physical Interactions with Object-Oriented Prediction and Planning , PDF: https://arxiv.org/pdf/1812.10972
Neural Material: Learning Elastic Constitutive Material and Damping Models from Sparse Data , PDF: https://arxiv.org/pdf/1808.04931
Discovering physical concepts with neural networks , PDF: https://arxiv.org/pdf/1807.10300
Fluid directed rigid body control using deep reinforcement learning , Project: http://gamma.cs.unc.edu/DRL_FluidRigid/
DeepMimic, Example-Guided Deep Reinforcement Learning of Physics-Based Character Skills , PDF: https://arxiv.org/pdf/1804.02717
Unsupervised Intuitive Physics from Visual Observations , PDF: https://arxiv.org/pdf/1805.05086
Graph networks as learnable physics engines for inference and control , PDF: https://arxiv.org/pdf/1806.01242
DeepWarp: DNN-based Nonlinear Deformation , PDF: https://arxiv.org/pdf/1803.09109
A proposal on machine learning via dynamical systems , Journal: https://link.springer.com/article/10.1007/s40304-017-0103-z
Interaction Networks for Learning about Objects, Relations and Physics , PDF: https://arxiv.org/pdf/1612.00222
Integrating Physics-Based Modeling with Machine Learning: A Survey , PDF: https://arxiv.org/pdf/2003.04919
Integrating Machine Learning with Physics-Based Modeling , PDF: https://arxiv.org/pdf/2006.02619
A review on Deep Reinforcement Learning for Fluid Mechanics , PDF: https://arxiv.org/pdf/1908.04127
Machine Learning for Fluid Mechanics , PDF: https://arxiv.org/pdf/1905.11075
phiflow: https://github.com/tum-pbs/phiflow
diff-taichi: https://github.com/yuanming-hu/difftaichi
jax-md: https://github.com/google/jax-md
Physics-based deep learning is a very dynamic field. Please let us know if we've overlooked papers that you think should be included by sending a mail to i15ge at cs.tum.de, and feel free to check out our homepage at https://ge.in.tum.de/.