Scimitar is a tool for verifying the safety of distributed protocols based on the technique of inductive proof decomposition, a compositional approach for developing an inductive invariant in a way that aids automated synthesis and interpretability of the inductive proof. It was primarily developed for targeting safety verification of distributed protocols, but works for any TLA+ specifications accepted by TLC. Correctness of discovered invariants is formally verified using the TLA+ proof system (TLAPS).
More details on the ideas underlying the techniques used here can also be found in this paper draft.
In order to run the tool you will need the following prerequisites:
- Java version >= 11
- Python 3 with pip installed
- Install Python dependencies with
python3 -m pip install -r requirements.txt - TLA+ Proof Manager (installation instructions)
Note that the scimitar tool makes use of a slightly modified version of the TLC model checker, whose source code can be found here. The binary of this modified version of TLC is included in this repo, so there is no need to download and build it manually.
As a demonstration of using scimitar, you can run it on the TwoPhase benchmark, a TLA+ specification of the two-phase commit protocol. This will attempt to generate an inductive invariant for proving the TCConsistent safety property:
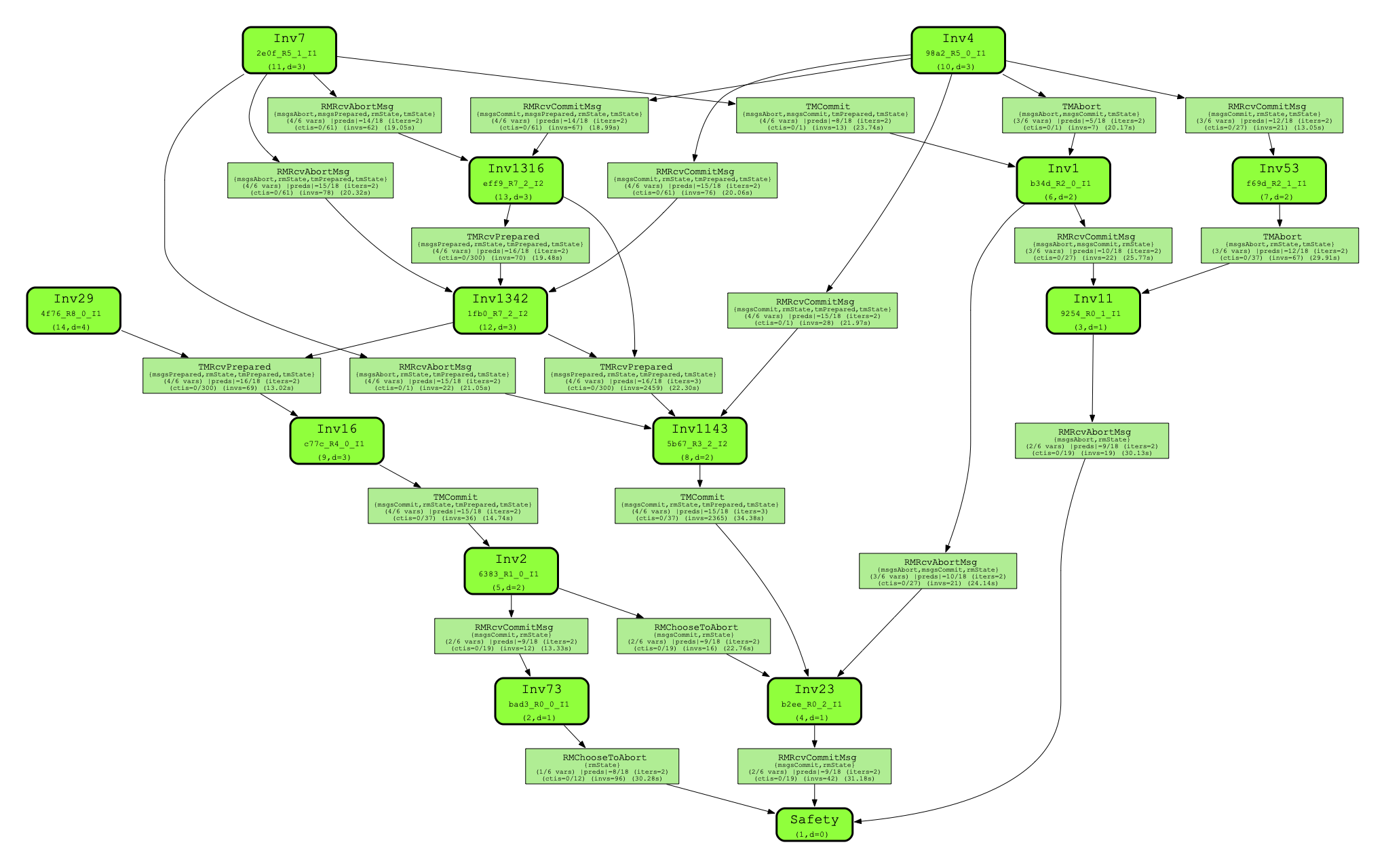
python3 scimitar.py --spec benchmarks/TwoPhase --seed 1 --num_simulate_traces 200000 --tlc_workers 6 --debug --target_sample_time_limit_ms 30000 --target_sample_states 200000 --opt_quant_minimize --k_cti_induction_depth 1 --ninvs 400000 --max_num_ctis_per_round 300 --save_dot --niters 5 --max_num_conjuncts_per_round 20 --num_ctigen_workers 7 --nrounds 45 --proof_tree_mode --auto_lemma_action_decomposition --enable_partitioned_state_caching --cti_elimination_workers 1 --do_tlaps_induction_checks --ninvs_per_iter_group 25000As the tool runs, it dynamically synthesizes an inductive proof graph, which is a compositional way of representing an inductive invariant in terms of its lemma and action relative induction dependencies. You can, for example, observe the graph as it is generated by opening benchmarks/TwoPhase_ind-proof-tree-sd1.pdf. An example of a completed proof graph for the TwoPhase protocol can be seen below:
This provides an intuitive way to understand the structure of the inductive invariant and proof, while also allowing for optimizations during synthesis.